高中数学第一章空间向量与立体几何章末整合课件新人教B版选择性必修第一册 1 28页

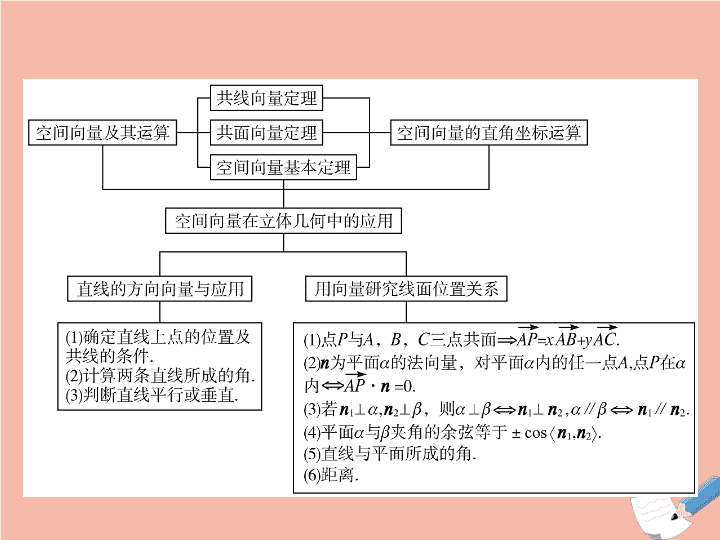
章末整合 专题一 专题二 专题三 专题一、空间向量的 运算 答案 : D 专题一 专题二 专题三 例 2 专题一 专题二 专题三 方法技巧 1 . 空间向量的概念及运算是由平面向量延伸而来的 , 要用类比的思想去掌握 , 在空间向量的加、减、数乘等线性运算中 , 要选择适当的向量为基底 , 用基向量表示出相关向量后再进行向量的运算 , 同时还要以相应的图形为指导 . 2 . 在求一个向量由其他几个向量来表示的时候 , 通常是利用向量的三角形法则、平行四边形法则和共线向量的特点 , 把所求的向量逐步分解最终归结为基底下的表示 . 专题一 专题二 专题三 答案 : C 专题一 专题二 专题三 变式训练 2 专题一 专题二 专题三 专题二、空间向量与线面位置关系 例 3 已知直三棱柱 ABC-A 1 B 1 C 1 中 , △ ABC 为等腰直角三角形 , ∠ BAC= 90 ° , 且 AB=AA 1 , D , E , F 分别为 B 1 A , C 1 C , BC 的中点 . (1) 求证 : DE ∥ 平面 ABC ; (2) 求证 : B 1 F ⊥ 平面 AEF. 专题一 专题二 专题三 证明 : 如图 , 建立空间直角坐标系 Axyz , 专题一 专题二 专题三 方法技巧 证明线面平行和垂直问题 , 可以用几何法 , 也可以用向量法 . 用向量法的关键在于构造向量 , 再用共线向量定理或共面向量定理及两向量垂直的判定定理 . 若能建立空间直角坐标系 , 其证法将更为灵活方便 . 专题一 专题二 专题三 变式训练 3 已知正方体 ABCD-A 1 B 1 C 1 D 1 , 求证 : (1) AD 1 ∥ 平面 BDC 1 ; 　 (2) A 1 C ⊥ 平面 BDC 1 . 证明 : 以 D 为坐标原点 , 建立如图所示的空间直角坐标系 Dxyz. 设正方体的棱长为 1, 则有 专题一 专题二 专题三 专题一 专题二 专题三 专题三、空间向量与空间角 例 4 如图 , 在三棱锥 S-ABC 中 , ∠ SAB= ∠ SAC= ∠ ACB= 90 ° , AC= 2 , 专题一 专题二 专题三 专题一 专题二 专题三 例 5 正方体 ABCD-A 1 B 1 C 1 D 1 中 , E 是 C 1 C 的中点 , 求 BE 与平面 B 1 BD 所成角的余弦值 . 专题一 专题二 专题三 专题一 专题二 专题三 例 6 如图 , 三棱柱 ABC-A 1 B 1 C 1 中 , 侧面 BB 1 C 1 C 为菱形 , AB ⊥ B 1 C. (1) 证明 : AC=AB 1 ; (2) 若 AC ⊥ AB 1 , ∠ CBB 1 = 60 ° , AB=BC , 求二面角 A-A 1 B 1 -C 1 的余弦值 . 专题一 专题二 专题三 (1) 证明 : 连接 BC 1 , 交 B 1 C 于点 O , 连接 AO , 因为侧面 BB 1 C 1 C 为菱形 , 所以 B 1 C ⊥ BC 1 , 且 O 为 B 1 C 及 BC 1 的中点 . 又 AB ⊥ B 1 C , 所以 B 1 C ⊥ 平面 ABO. 由于 AO ⊂ 平面 ABO , 故 B 1 C ⊥ AO. 又 B 1 O=CO , 故 AC=AB 1 . (2) 解 : 因为 AC ⊥ AB 1 , 且 O 为 B 1 C 的中点 , 所以 AO=CO. 又因为 AB=BC , 所以 △ BOA ≌ △ BOC. 故 OA ⊥ OB , 从而 OA , OB , OB 1 两两互相垂直 . 专题一 专题二 专题三 专题一 专题二 专题三 方法技巧 1 . 线线角 (1) 用 “ 平移法 ” 作出异面直线所成角 ( 或其补角 ), 解三角形求角 . (2) 用 “ 向量法 ” 求两直线的方向向量所成的角 . 2 . 线面角 (1) 按定义作出线面角 ( 即找到斜线在平面内的射影 ), 解三角形 . (2) 求平面的法向量 , 利用直线的方向向量与平面的法向量所成的锐角和直线与平面所成角互余求线面角 . (3) 利用等体积法求点到面的距离 , 由距离与斜线段长的比值等于线面角的正弦值求线面角 . 专题一 专题二 专题三 3 . 二面角 (1) 可以用定义法作出平面角解决 , 也可以用射影定理 S 射 =S 斜 · cos θ ; (2) 向量法是解决二面角大小的常用方法 , 只要合理建系 , 将所求归结为向量运算 . 这三种空间角求解方法技巧均很多 , 学习中应以向量法为主 , 侧重渗透向量坐标法这一特色 . 专题一 专题二 专题三 变式训练 4 如图 , 在长方体 ABCD-A 1 B 1 C 1 D 1 中 , B 1 C 和 C 1 D 与底面所成的角分别为 60 ° 和 45 ° , 则异面直线 B 1 C 和 C 1 D 所成角的余弦值为 　　　　　 .   专题一 专题二 专题三 专题一 专题二 专题三 专题一 专题二 专题三 专题一 专题二 专题三 变式训练 6 如图 , 四棱锥 P-ABCD 中 , PA ⊥ 底面 ABCD , BC=CD= 2, AC= 4, ∠ ACB= ∠ ACD = , F 为 PC 的中点 , AF ⊥ PB. (1) 求 PA 的长 ; (2) 求二面角 B-AF-D 的正弦值 . 专题一 专题二 专题三 专题一 专题二 专题三