2020届高考数学大二轮复习层级二专题四立体几何第3讲立体几何中的向量方法课时作业理 7页

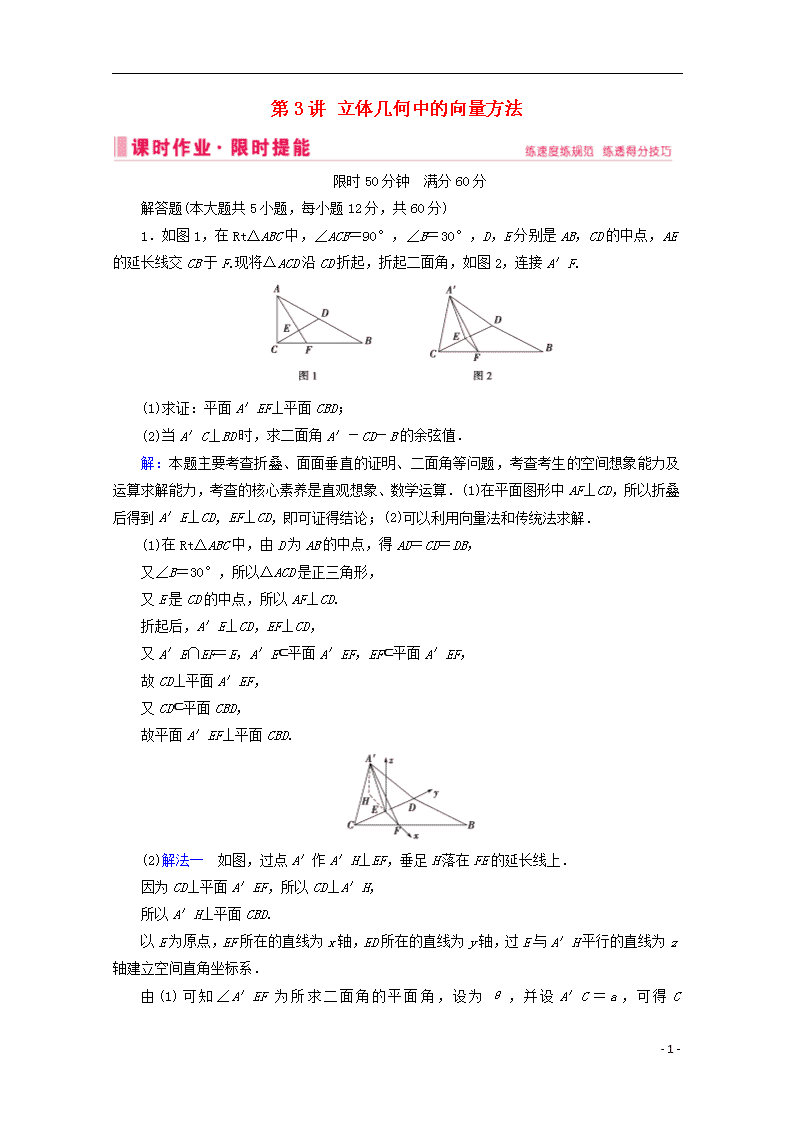
第3讲 立体几何中的向量方法 限时50分钟　满分60分 解答题(本大题共5小题，每小题12分，共60分)‎ ‎1．如图1，在Rt△ABC中，∠ACB＝90°，∠B＝30°，D，E分别是AB，CD的中点，AE的延长线交CB于F.现将△ACD沿CD折起，折起二面角，如图2，连接A′F.‎ ‎(1)求证：平面A′EF⊥平面CBD；‎ ‎(2)当A′C⊥BD时，求二面角A′－CD－B的余弦值．‎ 解：本题主要考查折叠、面面垂直的证明、二面角等问题，考查考生的空间想象能力及运算求解能力，考查的核心素养是直观想象、数学运算．(1)在平面图形中AF⊥CD，所以折叠后得到A′E⊥CD，EF⊥CD，即可证得结论；(2)可以利用向量法和传统法求解．‎ ‎(1)在Rt△ABC中，由D为AB的中点，得AD＝CD＝DB，‎ 又∠B＝30°，所以△ACD是正三角形，‎ 又E是CD的中点，所以AF⊥CD.‎ 折起后，A′E⊥CD，EF⊥CD，‎ 又A′E∩EF＝E，A′E⊂平面A′EF，EF⊂平面A′EF，‎ 故CD⊥平面A′EF，‎ 又CD⊂平面CBD，‎ 故平面A′EF⊥平面CBD.‎ ‎(2)解法一　如图，过点A′作A′H⊥EF，垂足H落在FE的延长线上．‎ 因为CD⊥平面A′EF，所以CD⊥A′H，‎ 所以A′H⊥平面CBD.‎ 以E为原点，EF所在的直线为x轴，ED所在的直线为y轴，过E与A′H平行的直线为z轴建立空间直角坐标系．‎ 由(1)可知∠A′EF为所求二面角的平面角，设为θ，并设A′C＝a，可得 - 7 -‎ C，D，B，A′.‎ 故＝，＝，因为A′C⊥BD，所以·＝0，‎ 即cos θ＋＝0，‎ 得cos θ＝－.‎ 故二面角A′－CD－B的余弦值为－.‎ 解法二　‎ 如图，过点A′作A′H⊥EF，垂足H落在FE的延长线上，‎ 因为CD⊥平面A′EF，所以CD⊥A′H，‎ 所以A′H⊥平面CBD.‎ 连接CH并延长交BD的延长线于G，‎ 由A′C⊥BD，得CH⊥BD，‎ 即∠CGB＝90°，‎ 因此△CEH～△CGD，‎ 则＝，‎ 设A′C＝a，易得∠GDC＝60°，DG＝，CE＝，CG＝，‎ 代入＝得EH＝，又EA′＝，故cos∠HEA′＝＝.‎ 又A′E⊥CD，EF⊥CD，‎ 所以∠A′EF即所求二面角的平面角，‎ 故二面角A′－CD－B的余弦值为－.‎ ‎2．(2019·北京卷)‎ - 7 -‎ 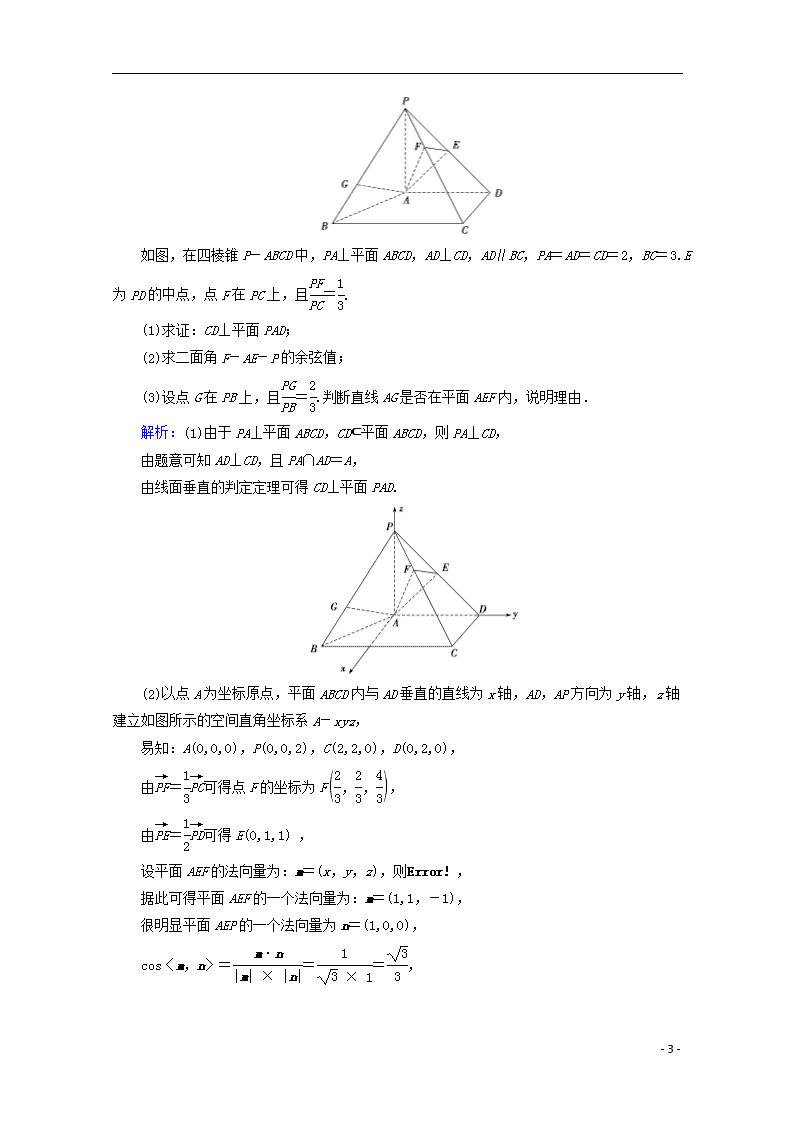如图，在四棱锥P－ABCD中，PA⊥平面ABCD，AD⊥CD，AD∥BC，PA＝AD＝CD＝2，BC＝3.E为PD的中点，点F在PC上，且＝.‎ ‎(1)求证：CD⊥平面PAD；‎ ‎(2)求二面角F－AE－P的余弦值；‎ ‎(3)设点G在PB上，且＝.判断直线AG是否在平面AEF内，说明理由．‎ 解析：(1)由于PA⊥平面ABCD，CD⊂平面ABCD，则PA⊥CD，‎ 由题意可知AD⊥CD，且PA∩AD＝A，‎ 由线面垂直的判定定理可得CD⊥平面PAD.‎ ‎(2)以点A为坐标原点，平面ABCD内与AD垂直的直线为x轴，AD，AP方向为y轴，z轴建立如图所示的空间直角坐标系A－xyz，‎ 易知：A(0,0,0)，P(0,0,2)，C(2,2,0)，D(0,2,0)，‎ 由＝可得点F的坐标为F，‎ 由＝可得E(0,1,1) ，‎ 设平面AEF的法向量为：m＝(x，y，z)，则 ，‎ 据此可得平面AEF的一个法向量为：m＝(1,1，－1)，‎ 很明显平面AEP的一个法向量为n＝(1,0,0)，‎ cos〈m，n〉＝＝＝，‎ 二面角F－AE－P的平面角为锐角，故二面角F－AE－P的余弦值为.‎ - 7 -‎ ‎(3)易知P(0,0,2)，B(2，－1,0)，由＝可得G，‎ 则＝，‎ 注意到平面AEF的一个法向量为：m＝(1,1，－1)，‎ 其m·＝0且点A在平面AEF内，故直线AG在平面AEF内．‎ ‎3．(2019·苏州三模)‎ 如图，在四棱锥PABCD中，PA⊥平面ABCD，AD∥BC，AD⊥CD，且AD＝CD＝，BC＝2，PA＝2.‎ ‎(1)取PC中点N，连接DN，求证：DN∥平面PAB.‎ ‎(2)求直线AC与PD所成角的余弦值．‎ ‎(3)在线段PD上，是否存在一点M，使得二面角MACD的大小为45°，如果存在，求BM与平面MAC所成的角，如果不存在，请说明理由．‎ 解析：‎ 取BC的中点E，连接DE与AC，相交于点O，连接AE，易知AC⊥DE，建立如图所示的空间直角坐标系，则A(0，－1,0)，B(2，－1,0)，C(0，1,0)，D(－1,0,0)，P(0，－1,2)，‎ ‎(1)PC中点N(0,0,1)，所以＝(1,0,1)，‎ 设平面PAB的法向量为n＝(a，b，c)，‎ 由＝(0,0,2)，＝(2,0,0)，‎ 令b＝1，可得：n＝(0,1,0)，所以·n＝0，因为DN⊄平面PAB，所以DN∥平面PAB.‎ ‎(2)＝(0,2,0)，＝(－1,1，－2)，设AC与PD所成的角为θ，则cos θ＝＝.‎ - 7 -‎ ‎(3)设M(x，y，z)及＝λ(0≤λ≤1)，‎ 所以⇒M(－λ，λ－1,2(1－λ))，‎ 设平面ACM的法向量为m＝(x，y，z)，‎ 由＝(0,2,0)，＝(－λ，λ，2(1－λ))，可得m＝(2－2λ，0，λ)，平面ACD的法向量为p＝(0,0,1)，‎ 所以cos〈m，p〉＝ ‎＝⇒λ＝ ，解得λ＝.‎ 解得M，‎ 所以＝，所以m＝，‎ 设BM与平面MAC所成角为φ，所以sin φ＝|cos〈，m〉|＝＝，所以φ＝.‎ ‎4．(2020·山东实验中学模拟)某工厂欲加工一件艺术品，需要用到三棱锥形状的坯材，工人将如图所示的长方体ABCD－EFQH材料切割成三棱锥H－ACF.‎ ‎(1)若点M，N，K分别是棱HA，HC，HF的中点，点G是NK上的任意一点，求证：MG∥平面ACF；‎ ‎(2)已知原长方体材料中，AB＝2，AD＝3，DH＝1，根据艺术品加工需要，工程师必须求出三棱锥H－ACF的高．甲工程师先求出AH所在直线与平面ACF所成的角θ，再根据公式h＝AH·sin θ，求三棱锥H－ACF的高h.请你根据甲工程师的思路，求该三棱锥的高．‎ 解：证明：(1)∵HM＝MA，HN＝NC，HK＝KF，‎ ‎∴MK∥AF，MN∥AC.∵MK⊄平面ACF，AF⊂平面ACF，‎ ‎∴MK∥平面ACF.‎ ‎∵MN⊄平面ACF，AC⊂平面ACF，∴MN∥平面ACF.‎ ‎∵MN，MK⊂平面MNK，且MK∩MN＝M，‎ - 7 -‎ ‎∴平面MNK∥平面ACF.‎ 又∵MG⊂平面MNK，∴MG∥平面ACF.‎ ‎(2)如图，以点D为坐标原点，分别以DA，DC，DH所在直线为x轴，y轴，z轴建立空间直角坐标系D－xyz.‎ 则有A(3,0,0)，C(0,2,0)，F(3,2,1)，H(0,0,1)，‎ ＝(－3,2,0)，＝(0,2,1)，＝(－3,0,1)．‎ 设平面ACF的一个法向量为n＝(x，y，z)，‎ ‎ 则有令y＝3，则n＝(2,3，－6)，‎ ‎∴sin θ＝＝＝，‎ ‎∴三棱锥H－ACF的高为AH·sin θ＝×＝.‎ ‎5.‎ 如图，四边形ABCD为菱形，G为AC与BD的交点，BE⊥平面ABCD.‎ ‎(1)证明：平面AEC⊥平面BED；‎ ‎(2)若∠ABC＝120°，AE⊥EC，三棱锥E－ACD的体积为，求该三棱锥的侧面积．‎ 解析：(1)因为四边形ABCD为菱形，所以AC⊥BD.‎ 因为BE⊥平面ABCD，所以AC⊥BE，又BD∩BE＝B，‎ 故AC⊥平面BED.‎ 又AC⊂平面AEC，‎ 所以平面AEC⊥平面BED.‎ ‎(2)设AB＝x，在菱形ABCD中，由∠ABC＝120°，可得AG＝GC＝x，GB＝GD＝.‎ 因为AE⊥EC，所以在Rt△AEC中，可得EG＝x.‎ - 7 -‎ 由BE⊥平面ABCD，知△EBG为直角三角形，可得BE＝x.‎ 由已知得，三棱锥E－ACD的体积VEACD＝×AC·GD·BE＝x3＝.故x＝2.‎ 从而可得AE＝EC＝ED＝.‎ 所以△EAC的面积为3，△EAD的面积与△ECD的面积均为.‎ 故三棱锥E－ACD的侧面积为3＋2.‎ - 7 -‎