2015年重庆市高考数学试卷（文科） 20页

‎2015年重庆市高考数学试卷（文科）‎ ‎　‎ 一、选择题：本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1．（5分）已知集合A={1，2，3}，B={1，3}，则A∩B=（　　）‎ A．{2} B．{1，2} C．{1，3} D．{1，2，3}‎ ‎2．（5分）“x=1”是“x2﹣2x+1=0”的（　　）‎ A．充要条件 B．充分而不必要条件 C．必要而不充分条件 D．既不充分也不必要条件 ‎3．（5分）函数f（x）=log2（x2+2x﹣3）的定义域是（　　）‎ A．[﹣3，1] B．（﹣3，1） C．（﹣∞，﹣3]∪[1，+∞） D．（﹣∞，﹣3）∪（1，+∞）‎ ‎4．（5分）重庆市2013年各月的平均气温（℃）数据的茎叶图如，则这组数据的中位数是（　　）‎ A．19 B．20 C．21.5 D．23‎ ‎5．（5分）某几何体的三视图如图所示，则该几何体的体积为（　　）‎ A． B． C． D．‎ ‎6．（5分）若tanα=，tan（α+β）=，则tanβ=（　　）‎ A． B． C． D．‎ ‎7．（5分）已知非零向量满足||=4||，且⊥（）则的夹角为（　　）‎ A． B． C． D．‎ ‎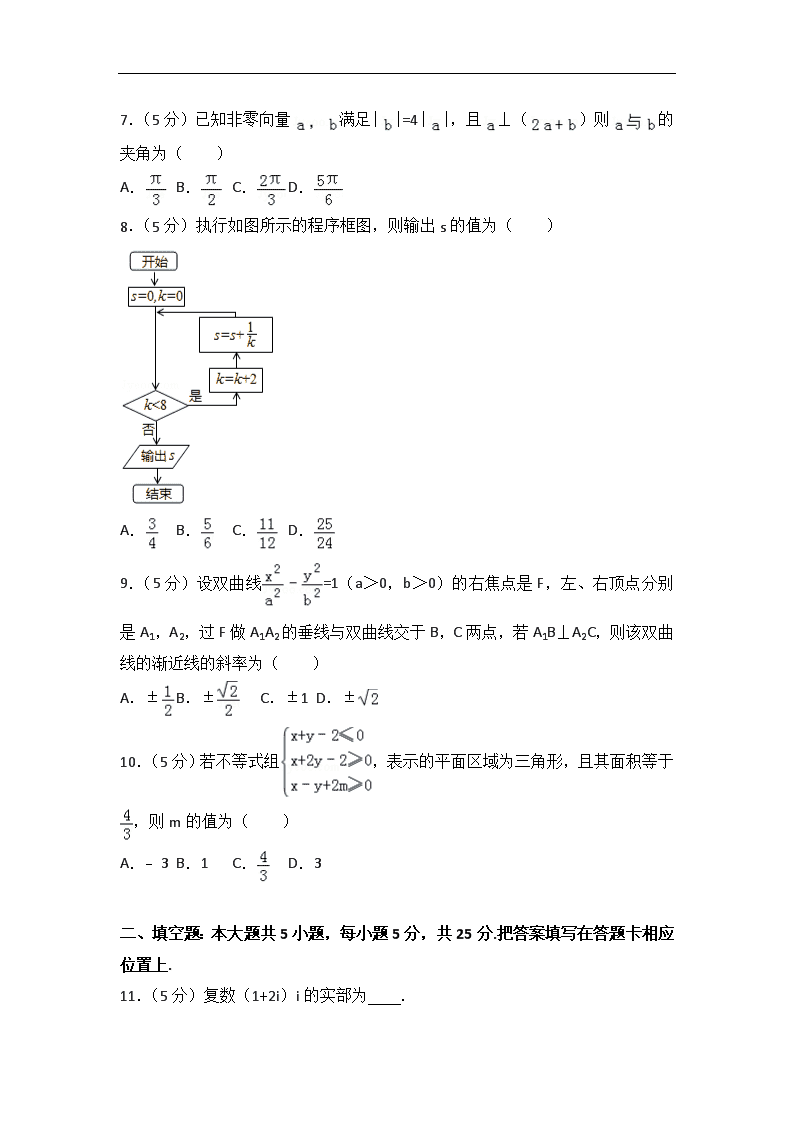8．（5分）执行如图所示的程序框图，则输出s的值为（　　）‎ A． B． C． D．‎ ‎9．（5分）设双曲线=1（a＞0，b＞0）的右焦点是F，左、右顶点分别是A1，A2，过F做A1A2的垂线与双曲线交于B，C两点，若A1B⊥A2C，则该双曲线的渐近线的斜率为（　　）‎ A．± B．± C．±1 D．±‎ ‎10．（5分）若不等式组，表示的平面区域为三角形，且其面积等于，则m的值为（　　）‎ A．﹣3 B．1 C． D．3‎ ‎　‎ 二、填空题：本大题共5小题，每小题5分，共25分.把答案填写在答题卡相应位置上.‎ ‎11．（5分）复数（1+2i）i的实部为　　．‎ ‎12．（5分）若点P（1，2）在以坐标原点为圆心的圆上，则该圆在点P处的切线方程为　　．‎ ‎13．（5分）设△ABC的内角A，B，C的对边分别为a，b，c，且a=2，cosC=﹣，3sinA=2sinB，则c=　　．‎ ‎14．（5分）设a，b＞0，a+b=5，则+的最大值为　　．‎ ‎15．（5分）在区间[0，5]上随机地选择一个数p，则方程x2+2px+3p﹣2=0有两个负根的概率为　　．‎ ‎　‎ 三、解答题：本大题共6小题，共75分，解答应写出文字说明、证明过程或演算步骤．‎ ‎16．（12分）已知等差数列{an}满足a3=2，前3项和S3=．‎ ‎（Ⅰ）求{an}的通项公式；‎ ‎（Ⅱ）设等比数列{bn}满足b1=a1，b4=a15，求{bn}前n项和Tn．‎ ‎17．（13分）随着我国经济的发展，居民的储蓄存款逐年增长．设某地区城乡居民人民币储蓄存款（年底余额）如下表：‎ 年份 ‎2010‎ ‎2011‎ ‎2012‎ ‎2013‎ ‎2014‎ 时间代号t ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 储蓄存款y（千亿元）‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎10‎ ‎（Ⅰ）求y关于t的回归方程=t+．‎ ‎（Ⅱ）用所求回归方程预测该地区2015年（t=6）的人民币储蓄存款．‎ 附：回归方程=t+中 ‎．‎ ‎18．（13分）已知函数f（x）=sin2x﹣cos2x．‎ ‎（Ⅰ）求f（x）的最小周期和最小值；‎ ‎（Ⅱ）将函数f（x）的图象上每一点的横坐标伸长到原来的两倍，纵坐标不变，得到函数g（x）的图象．当x∈时，求g（x）的值域．‎ ‎19．（12分）已知函数f（x）=ax3+x2（a∈R）在x=处取得极值．‎ ‎（Ⅰ）确定a的值；‎ ‎（Ⅱ）若g（x）=f（x）ex，讨论g（x）的单调性．‎ ‎20．（12分）如题图，三棱锥P﹣ABC中，平面PAC⊥平面ABC，∠ABC=，点D、E在线段AC上，且AD=DE=EC=2，PD=PC=4，点F在线段AB上，且EF∥BC．‎ ‎（Ⅰ）证明：AB⊥平面PFE．‎ ‎（Ⅱ）若四棱锥P﹣DFBC的体积为7，求线段BC的长．‎ ‎21．（13分）如题图，椭圆=1（a＞b＞0）的左右焦点分别为F1，F2，且过F2的直线交椭圆于P，Q两点，且PQ⊥PF1．‎ ‎（Ⅰ）若|PF1|=2+，|PF2|=2﹣，求椭圆的标准方程．‎ ‎（Ⅱ）若|PQ|=λ|PF1|，且≤λ＜，试确定椭圆离心率e的取值范围．‎ ‎　‎ ‎2015年重庆市高考数学试卷（文科）‎ 参考答案与试题解析 ‎　‎ 一、选择题：本大题共10小题，每小题5分，共50分，在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1．（5分）（2015•重庆）已知集合A={1，2，3}，B={1，3}，则A∩B=（　　）‎ A．{2} B．{1，2} C．{1，3} D．{1，2，3}‎ ‎【分析】直接利用集合的交集的求法求解即可．‎ ‎【解答】解：集合A={1，2，3}，B={1，3}，则A∩B={1，3}．‎ 故选：C．‎ ‎　‎ ‎2．（5分）（2015•重庆）“x=1”是“x2﹣2x+1=0”的（　　）‎ A．充要条件 B．充分而不必要条件 C．必要而不充分条件 D．既不充分也不必要条件 ‎【分析】先求出方程x2﹣2x+1=0的解，再和x=1比较，从而得到答案．‎ ‎【解答】解：由x2﹣2x+1=0，解得：x=1，‎ 故“x=1”是“x2﹣2x+1=0”的充要条件，‎ 故选：A．‎ ‎　‎ ‎3．（5分）（2015•重庆）函数f（x）=log2（x2+2x﹣3）的定义域是（　　）‎ A．[﹣3，1] B．（﹣3，1） C．（﹣∞，﹣3]∪[1，+∞） D．（﹣∞，﹣3）∪（1，+∞）‎ ‎【分析】利用对数函数的真数大于0求得函数定义域．‎ ‎【解答】解：由题意得：x2+2x﹣3＞0，即（x﹣1）（x+3）＞0‎ 解得x＞1或x＜﹣3‎ 所以定义域为（﹣∞，﹣3）∪（1，+∞）‎ 故选D．‎ ‎　‎ ‎4．（5分）（2015•重庆）重庆市2013年各月的平均气温（℃）数据的茎叶图如，则这组数据的中位数是（　　）‎ A．19 B．20 C．21.5 D．23‎ ‎【分析】根据中位数的定义进行求解即可．‎ ‎【解答】解：样本数据有12个，位于中间的两个数为20，20，‎ 则中位数为，‎ 故选：B ‎　‎ ‎5．（5分）（2015•重庆）某几何体的三视图如图所示，则该几何体的体积为（　　）‎ A． B． C． D．‎ ‎【分析】利用三视图判断直观图的形状，结合三视图的数据，求解几何体的体积即可．‎ ‎【解答】解：由题意可知几何体的形状是放倒的圆柱，底面半径为1，高为2，左侧与一个底面半径为1，高为1的半圆锥组成的组合体，‎ 几何体的体积为：=．‎ 故选：B．‎ ‎　‎ ‎6．（5分）（2015•重庆）若tanα=，tan（α+β）=，则tanβ=（　　）‎ A． B． C． D．‎ ‎【分析】由条件利用查两角差的正切公式，求得tanβ=tan[（α+β）﹣α]的值．‎ ‎【解答】解：∵tanα=，tan（α+β）=，则tanβ=tan[（α+β）﹣α]===，‎ 故选：A．‎ ‎　‎ ‎7．（5分）（2015•重庆）已知非零向量满足||=4||，且⊥（）则的夹角为（　　）‎ A． B． C． D．‎ ‎【分析】由已知向量垂直得到数量积为0，于是得到非零向量的模与夹角的关系，求出夹角的余弦值．‎ ‎【解答】解：由已知非零向量满足||=4||，且⊥（），设两个非零向量的夹角为θ，‎ 所以•（）=0，即2=0，所以cosθ=，θ∈[0，π]，所以；‎ 故选C．‎ ‎　‎ ‎8．（5分）（2015•重庆）执行如图所示的程序框图，则输出s的值为（　　）‎ A． B． C． D．‎ ‎【分析】模拟执行程序框图，依次写出每次循环得到的k，s的值，当k=8时不满足条件k＜8，退出循环，输出s的值为．‎ ‎【解答】解：模拟执行程序框图，可得 s=0，k=0‎ 满足条件k＜8，k=2，s=‎ 满足条件k＜8，k=4，s=+‎ 满足条件k＜8，k=6，s=++‎ 满足条件k＜8，k=8，s=+++=‎ 不满足条件k＜8，退出循环，输出s的值为．‎ 故选：D．‎ ‎　‎ ‎9．（5分）（2015•重庆）设双曲线=1（a＞0，b＞0）的右焦点是F，左、右顶点分别是A1，A2，过F做A1A2的垂线与双曲线交于B，C两点，若A1B⊥A2C，则该双曲线的渐近线的斜率为（　　）‎ A．± B．± C．±1 D．±‎ ‎【分析】求得A1（﹣a，0），A2（a，0），B（c，），C（c，﹣），利用A1B⊥‎ A2C，可得，求出a=b，即可得出 双曲线的渐近线的斜率．‎ ‎【解答】解：由题意，A1（﹣a，0），A2（a，0），B（c，），C（c，﹣），‎ ‎∵A1B⊥A2C，‎ ‎∴，‎ ‎∴a=b，‎ ‎∴双曲线的渐近线的斜率为±1．‎ 故选：C．‎ ‎　‎ ‎10．（5分）（2015•重庆）若不等式组，表示的平面区域为三角形，且其面积等于，则m的值为（　　）‎ A．﹣3 B．1 C． D．3‎ ‎【分析】作出不等式组对应的平面区域，求出三角形各顶点的坐标，利用三角形的面积公式进行求解即可．‎ ‎【解答】解：作出不等式组对应的平面区域如图：‎ 若表示的平面区域为三角形，‎ 由，得，即A（2，0），‎ 则A（2，0）在直线x﹣y+2m=0的下方，‎ 即2+2m＞0，‎ 则m＞﹣1，‎ 则A（2，0），D（﹣2m，0），‎ 由，解得，即B（1﹣m，1+m），‎ 由，解得，即C（，）．‎ 则三角形ABC的面积S△ABC=S△ADB﹣S△ADC ‎ ‎=|AD||yB﹣yC|‎ ‎=（2+2m）（1+m﹣）‎ ‎=（1+m）（1+m﹣）=，‎ 即（1+m）×=，‎ 即（1+m）2=4‎ 解得m=1或m=﹣3（舍），‎ 故选：B ‎　‎ 二、填空题：本大题共5小题，每小题5分，共25分.把答案填写在答题卡相应位置上.‎ ‎11．（5分）（2015•重庆）复数（1+2i）i的实部为　﹣2　．‎ ‎【分析】利用复数的运算法则化简为a+bi的形式，然后找出实部；注意i2=﹣1．‎ ‎【解答】解：（1+2i）i=i+2i2=﹣2+i，所以此复数的实部为﹣2；‎ 故答案为：﹣2．‎ ‎　‎ ‎12．（5分）（2015•重庆）若点P（1，2）在以坐标原点为圆心的圆上，则该圆在点P处的切线方程为　x+2y﹣5=0　．‎ ‎【分析】由条件利用直线和圆相切的性质，两条直线垂直的性质求出切线的斜率，再利用点斜式求出该圆在点P处的切线的方程．‎ ‎【解答】解：由题意可得OP和切线垂直，故切线的斜率为﹣==﹣，‎ 故切线的方程为y﹣2=﹣（x﹣1），即 x+2y﹣5=0，‎ 故答案为：x+2y﹣5=0．‎ ‎　‎ ‎13．（5分）（2015•重庆）设△ABC的内角A，B，C的对边分别为a，b，c，且a=2，cosC=﹣，3sinA=2sinB，则c=　4　．‎ ‎【分析】由3sinA=2sinB即正弦定理可得3a=2b，由a=2，即可求得b，利用余弦定理结合已知即可得解．‎ ‎【解答】解：∵3sinA=2sinB，‎ ‎∴由正弦定理可得：3a=2b，‎ ‎∵a=2，‎ ‎∴可解得b=3，‎ 又∵cosC=﹣，‎ ‎∴由余弦定理可得：c2=a2+b2﹣2abcosC=4+9﹣2×=16，‎ ‎∴解得：c=4．‎ 故答案为：4．‎ ‎　‎ ‎14．（5分）（2015•重庆）设a，b＞0，a+b=5，则+的最大值为　3　．‎ ‎【分析】利用柯西不等式，即可求出的最大值．‎ ‎【解答】解：由题意，（）2≤（1+1）（a+1+b+3）=18，‎ ‎∴的最大值为3，‎ 故答案为：3．‎ ‎　‎ ‎15．（5分）（2015•重庆）在区间[0，5]上随机地选择一个数p，则方程x2+2px+3p﹣2=0有两个负根的概率为　　．‎ ‎【分析】由一元二次方程根的分布可得p的不等式组，解不等式组，由长度之比可得所求概率．‎ ‎【解答】解：方程x2+2px+3p﹣2=0有两个负根等价于，‎ 解关于p的不等式组可得＜p≤1或p≥2，‎ ‎∴所求概率P==‎ 故答案为：‎ ‎　‎ 三、解答题：本大题共6小题，共75分，解答应写出文字说明、证明过程或演算步骤．‎ ‎16．（12分）（2015•重庆）已知等差数列{an}满足a3=2，前3项和S3=．‎ ‎（Ⅰ）求{an}的通项公式；‎ ‎（Ⅱ）设等比数列{bn}满足b1=a1，b4=a15，求{bn}前n项和Tn．‎ ‎【分析】（Ⅰ）设等差数列{an}的公差为d，则由已知条件列式求得首项和公差，代入等差数列的通项公式得答案；‎ ‎（Ⅱ）求出，再求出等比数列的公比，由等比数列的前n项和公式求得{bn}前n项和Tn．‎ ‎【解答】解：（Ⅰ）设等差数列{an}的公差为d，则由已知条件得：‎ ‎，解得．‎ 代入等差数列的通项公式得：；‎ ‎（Ⅱ）由（Ⅰ）得，．‎ 设{bn}的公比为q，则，从而q=2，‎ 故{bn}的前n项和．‎ ‎　‎ ‎17．（13分）（2015•重庆）随着我国经济的发展，居民的储蓄存款逐年增长．设某地区城乡居民人民币储蓄存款（年底余额）如下表：‎ 年份 ‎2010‎ ‎2011‎ ‎2012‎ ‎2013‎ ‎2014‎ 时间代号t ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ 储蓄存款y（千亿元）‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎10‎ ‎（Ⅰ）求y关于t的回归方程=t+．‎ ‎（Ⅱ）用所求回归方程预测该地区2015年（t=6）的人民币储蓄存款．‎ 附：回归方程=t+中 ‎．‎ ‎【分析】（Ⅰ）利用公式求出a，b，即可求y关于t的回归方程=t+．‎ ‎（Ⅱ）t=6，代入回归方程，即可预测该地区2015年的人民币储蓄存款．‎ ‎【解答】解：（Ⅰ）‎ 由题意，=3，=7.2，‎ ‎=55﹣5×32=10，=120﹣5×3×7.2=12，‎ ‎∴=1.2，=7.2﹣1.2×3=3.6，‎ ‎∴y关于t的回归方程=1.2t+3.6．‎ ‎（Ⅱ）t=6时，=1.2×6+3.6=10.8（千亿元）．‎ ‎　‎ ‎18．（13分）（2015•重庆）已知函数f（x）=sin2x﹣cos2x．‎ ‎（Ⅰ）求f（x）的最小周期和最小值；‎ ‎（Ⅱ）将函数f（x）的图象上每一点的横坐标伸长到原来的两倍，纵坐标不变，得到函数g（x）的图象．当x∈时，求g（x）的值域．‎ ‎【分析】（Ⅰ）由三角函数中的恒等变换应用化简函数解析式可得f（x）=sin（2x﹣）﹣，从而可求最小周期和最小值；‎ ‎（Ⅱ）由函数y=Asin（ωx+φ）的图象变换可得g（x）=sin（x﹣）﹣，由x∈[，π]时，可得x﹣的范围，即可求得g（x）的值域．‎ ‎【解答】解：（Ⅰ）∵f（x）=sin2x﹣cos2x=sin2x﹣（1+cos2x）=sin（2x﹣）﹣，‎ ‎∴f（x）的最小周期T==π，最小值为：﹣1﹣=﹣．‎ ‎（Ⅱ）由条件可知：g（x）=sin（x﹣）﹣‎ 当x∈[，π]时，有x﹣∈[，]，从而sin（x﹣）的值域为[，1]，那么sin（x﹣）﹣的值域为：[，]，‎ 故g（x）在区间[，π]上的值域是[，]．‎ ‎　‎ ‎19．（12分）（2015•重庆）已知函数f（x）=ax3+x2（a∈R）在x=处取得极值．‎ ‎（Ⅰ）确定a的值；‎ ‎（Ⅱ）若g（x）=f（x）ex，讨论g（x）的单调性．‎ ‎【分析】（Ⅰ）求导数，利用f（x）=ax3+x2（a∈R）在x=处取得极值，可得f′（﹣）=0，即可确定a的值；‎ ‎（Ⅱ）由（Ⅰ）得g（x）=（x3+x2）ex，利用导数的正负可得g（x）的单调性．‎ ‎【解答】解：（Ⅰ）对f（x）求导得f′（x）=3ax2+2x．‎ ‎∵f（x）=ax3+x2（a∈R）在x=处取得极值，‎ ‎∴f′（﹣）=0，‎ ‎∴3a•+2•（﹣）=0，‎ ‎∴a=；‎ ‎（Ⅱ）由（Ⅰ）得g（x）=（x3+x2）ex，‎ ‎∴g′（x）=（x2+2x）ex+（x3+x2）ex=x（x+1）（x+4）ex，‎ 令g′（x）=0，解得x=0，x=﹣1或x=﹣4，‎ 当x＜﹣4时，g′（x）＜0，故g（x）为减函数；‎ 当﹣4＜x＜﹣1时，g′（x）＞0，故g（x）为增函数；‎ 当﹣1＜x＜0时，g′（x）＜0，故g（x）为减函数；‎ 当x＞0时，g′（x）＞0，故g（x）为增函数；‎ 综上知g（x）在（﹣∞，﹣4）和（﹣1，0）内为减函数，在（﹣4，﹣1）和（0，+∞）内为增函数．‎ ‎　‎ ‎20．（12分）（2015•重庆）如题图，三棱锥P﹣ABC中，平面PAC⊥平面ABC，∠ABC=，点D、E在线段AC上，且AD=DE=EC=2，PD=PC=4，点F在线段AB上，且EF∥BC．‎ ‎（Ⅰ）证明：AB⊥平面PFE．‎ ‎（Ⅱ）若四棱锥P﹣DFBC的体积为7，求线段BC的长．‎ ‎【分析】（Ⅰ）由等腰三角形的性质可证PE⊥AC，可证PE⊥AB．又EF∥BC，可证AB⊥EF，从而AB与平面PEF内两条相交直线PE，EF都垂直，可证AB⊥平面PEF．‎ ‎（Ⅱ）设BC=x，可求AB，S△ABC，由EF∥BC可得△AFE∽△ABC，求得S△AFE=S△ABC，由AD=AE，可求S△AFD，从而求得四边形DFBC的面积，由（Ⅰ）知PE为四棱锥P﹣DFBC的高，求得PE，由体积VP﹣DFBC=SDFBC•PE=7，即可解得线段BC的长．‎ ‎【解答】解：（Ⅰ）如图，由DE=EC，PD=PC知，E为等腰△PDC中DC边的中点，故PE⊥AC，‎ 又平面PAC⊥平面ABC，平面PAC∩平面ABC=AC，PE⊂平面PAC，PE⊥AC，‎ 所以PE⊥平面ABC，从而PE⊥AB．‎ 因为∠ABC=，EF∥BC，‎ 故AB⊥EF，‎ 从而AB与平面PEF内两条相交直线PE，EF都垂直，‎ 所以AB⊥平面PEF．‎ ‎（Ⅱ）设BC=x，则在直角△ABC中，AB==，‎ 从而S△ABC=AB•BC=x，‎ 由EF∥BC知，得△AFE∽△ABC，‎ 故=（）2=，即S△AFE=S△ABC，‎ 由AD=AE，S△AFD==S△ABC=S△ABC=x，‎ 从而四边形DFBC的面积为：SDFBC=S△ABC﹣SAFD=x﹣x=x．‎ 由（Ⅰ）知，PE⊥平面ABC，所以PE为四棱锥P﹣DFBC的高．‎ 在直角△PEC中，PE===2，‎ 故体积VP﹣DFBC=SDFBC•PE=x=7，‎ 故得x4﹣36x2+243=0，解得x2=9或x2=27，由于x＞0，可得x=3或x=3．‎ 所以：BC=3或BC=3．‎ ‎　‎ ‎21．（13分）（2015•重庆）如题图，椭圆=1（a＞b＞0）的左右焦点分别为F1，F2，且过F2的直线交椭圆于P，Q两点，且PQ⊥PF1．‎ ‎（Ⅰ）若|PF1|=2+，|PF2|=2﹣，求椭圆的标准方程．‎ ‎（Ⅱ）若|PQ|=λ|PF1|，且≤λ＜，试确定椭圆离心率e的取值范围．‎ ‎【分析】（I）由椭圆的定义可得：2a=|PF1|+|PF2|，解得a．设椭圆的半焦距为c，由于PQ⊥PF1，利用勾股定理可得2c=|F1F2|=，解得c．利用b2=a2﹣c2．即可得出椭圆的标准方程．‎ ‎（II）如图所示，由PQ⊥PF1，|PQ|=λ|PF1|，可得|QF1|=，由椭圆的定义可得：|PF1|+|PQ|+|QF1|=4a，解得|PF1|=．|PF2|=2a﹣|PF1|，由勾股定理可得：2c=|F1F2|=，代入化简．令t=1+λ，则上式化为e2=，解出即可．‎ ‎【解答】解：（I）由椭圆的定义可得：2a=|PF1|+|PF2|=（2+）+（2﹣）=4，解得a=2．‎ 设椭圆的半焦距为c，∵PQ⊥PF1，‎ ‎∴2c=|F1F2|===2，‎ ‎∴c=．‎ ‎∴b2=a2﹣c2=1．‎ ‎∴椭圆的标准方程为．‎ ‎（II）如图所示，由PQ⊥PF1，|PQ|=λ|PF1|，‎ ‎∴|QF1|==，‎ 由椭圆的定义可得：2a=|PF1|+|PF2|=|QF1|+|QF2|，‎ ‎∴|PF1|+|PQ|+|QF1|=4a，‎ ‎∴|PF1|=4a，解得|PF1|=．‎ ‎|PF2|=2a﹣|PF1|=，‎ 由勾股定理可得：2c=|F1F2|=，‎ ‎∴+=4c2，‎ ‎∴+=e2．‎ 令t=1+λ，则上式化为=，‎ ‎∵t=1+λ，且≤λ＜，‎ ‎∴t关于λ单调递增，∴3≤t＜4．∴，‎ ‎∴，解得．‎ ‎∴椭圆离心率的取值范围是．‎ ‎　‎ 参与本试卷答题和审题的老师有：qiss；刘老师；雪狼王；maths；caoqz；changq；w3239003；刘长柏；lincy；sxs123；沂蒙松（排名不分先后）‎ ‎2017年2月3日