2021版高考数学一轮复习第九章立体几何9-4垂直关系课件理北师大版 17页

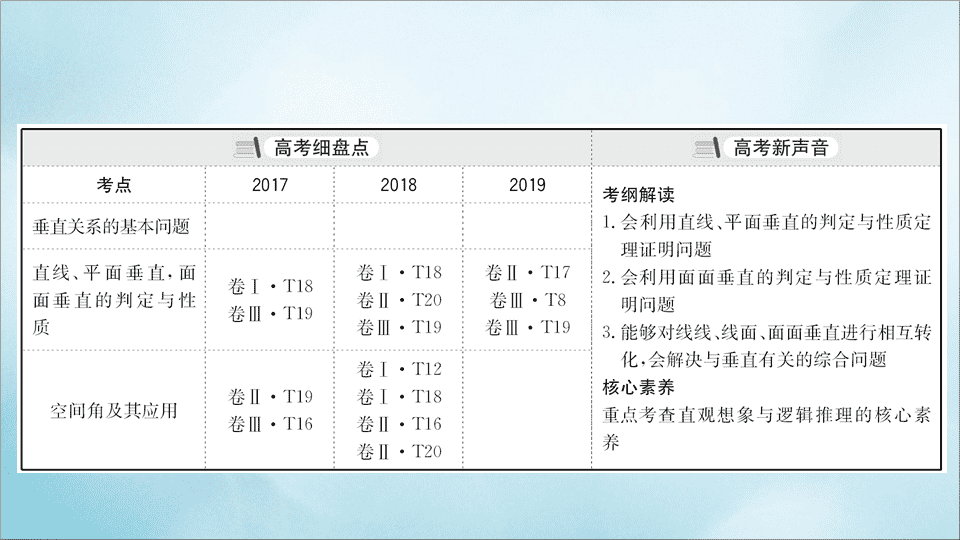
第四节　 垂 直 关 系 内容索引 必备知识 · 自主学习 核心考点 · 精准研析 核心素养 · 微专题 核心素养测评 【教材 · 知识梳理】 1. 直线与直线垂直 (1) 定义 : 若两条直线相交于一点或经过平移后相交于一点 , 并且交角为直角 , 则 称这两条直线互相垂直 . (2) 若一条直线垂直于一个平面 , 则它就和平面内的任意一条直线垂直 . 2. 直线与平面垂直 (1) 定义 : 如果一条直线和一个平面内的任何一条直线都垂直 , 那么称这条直线和 这个平面垂直 . (2) 判定定理与性质定理 : 3. 平面与平面垂直 【知识点辨析】 ( 正确的打 “ √ ” , 错误的打 “ × ” ) (1) 直线 l 与平面 α 内的无数条直线都垂直 , 则 l ⊥α. ( 　　 ) (2) 若两平行线中的一条垂直于一个平面 , 则另一条也垂直于这个平面 .( 　　 ) (3) 若直线 a⊥ 平面 α, 直线 b∥α, 则直线 a 与 b 垂直 . ( 　　 ) (4) 若 α⊥β,a⊥β, 则 a∥α. ( 　　 ) (5) 若两平面垂直 , 则其中一个平面内的任意一条直线垂直于另一个平面 .( 　　 ) (6) 如果两个平面所成的二面角为 90°, 则这两个平面垂直 . ( 　　 ) 提示 : (1) ×. 直线 l 与平面 α 内的任意一条直线都垂直 , 则 l ⊥α. (2)√. (3)√. (4)×. 若 α⊥β,a⊥β, 则 a∥α 或 a α. (5)×. 若两平面垂直 , 则其中一个平面内垂直于交线的直线垂直于另一个平面 . (6)√. 【易错点索引】 序号 易错警示 典题索引 1 证明线面垂直时忽视平面上的两条直线相交 考点一、 T3 考点三、角度 1 2 证明面面垂直时找错直线 考点一、 T3 3 应用面面垂直的性质定理时忽视与交线垂直 考点三、角度 2 【教材 · 基础自测】 1.( 必修 2P43B 组 T3 改编 ) 下列命题中不正确的是 ( 　　 ) A. 如果平面 α⊥ 平面 β, 且直线 l ∥ 平面 α, 则直线 l ⊥ 平面 β B. 如果平面 α⊥ 平面 β, 那么平面 α 内一定存在直线平行于平面 β C. 如果平面 α 不垂直于平面 β, 那么平面 α 内一定不存在直线垂直于平面 β D. 如果平面 α⊥ 平面 γ, 平面 β⊥ 平面 γ,α∩β= l , 那么 l ⊥γ 【解析】 选 A. 根据面面垂直的性质 , 知 A 不正确 , 直线 l 可能平行于平面 β, 也可能 在平面 β 内或与平面 β 相交 . 2.( 必修 2 P38 例 1 改编 ) 如图 , 在三棱锥 V-ABC 中 ,∠VAB=∠VAC=∠ABC=90°, 则构 成三棱锥的四个三角 形中直角三角形的个数为 　　　　 .  所以有 4 个直角三角形 . 答案 : 4 3.( 必修 2 P42T6 改编 ) 如图 , 已知平面 α,β, 且 α∩β=AB,PC⊥α,PD⊥β,C,D 是 垂足 . 那么直线 AB 与平面 PCD 的位置关系为 　　　　 , 若 PC=PD=1,CD= , 则平面 α 与平面 β 的位置关系为 　　　　 .  【解析】 因为 PC⊥α,AB α, 所以 PC⊥AB. 同理 PD⊥AB. 又 PC∩PD=P, 故 AB⊥ 平 面 PCD. 设 AB 与平面 PCD 的交点为 H, 连接 CH,DH. 因为 AB⊥ 平面 PCD, 所以 AB⊥CH, AB⊥DH, 所以 ∠CHD 是二面角 α-AB-β 的平面角 . 又 PC=PD=1,CD= , 所以 CD 2 = PC 2 +PD 2 =2, 即 ∠CPD=90°. 在平面四边形 PCHD 中 ,∠PCH=∠PDH=∠CPD=90°, 所以 ∠CHD=90°. 故平面 α⊥ 平面 β. 答案 : AB⊥ 平面 PCD 　平面 α⊥ 平面 β 核心素养　逻辑推理 —— 逻辑推理心路历程　   【素养诠释】 逻辑推理是指从一些事实和命题出发 , 依据逻辑规则推出一个命题的过程 , 主要包括两类 : 一类是从特殊到一般的推理 , 推理形式主要有归纳、类比 ; 一类是从一般到特殊的推理 . 【典例】 (2019· 全国卷 Ⅲ) 如图 , 点 N 为正方形 ABCD 的中心 ,△ECD 为正三角形 , 平面 ECD⊥ 平面 ABCD,M 是线段 ED 的中点 , 则 ( 　　 ) A.BM=EN, 且直线 BM,EN 是相交直线 B.BM≠EN, 且直线 BM,EN 是相交直线 C.BM=EN, 且直线 BM,EN 是异面直线 D.BM≠EN, 且直线 BM,EN 是异面直线 【素养立意 】 本题要求证的结论是线段 BM 与 EN 的大小关系及位置关系 , 我们可以假定相交 , 那么需要找到它们所确定的平面 , 进而通过已知条件进行逻辑推理论证 . 【解析】 选 B. 连接 BD, 则点 N 在 BD 上且为 BD 中点 . 因为直线 BM,EN 都是平面 BED 内 的直线 , 且不平行 , 即直线 BM,EN 是相交直线 . 设正方形 ABCD 的边长为 2a, 则由题 意可得 :DE=2a,DM=a,DN= a,DB=2 a, 根据余弦定理可得 :BM 2 =DB 2 +DM 2 - 2DB·DMcos∠BDE=9a 2 -4 a 2 cos∠BDE,EN 2 =DE 2 +DN 2 -2DE·DNcos∠BDE=6a 2 - 4 a 2 cos∠BDE, 所以 BM≠EN.