2020_2021学年新教材高中数学第一章空间向量与立体几何1 44页

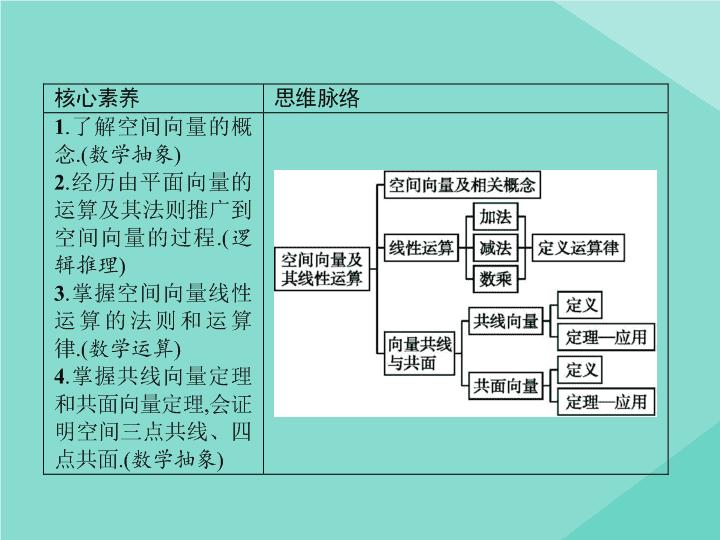
1.1.1 　空间向量及其线性运算 激趣诱思 知识点拨 一天 , 梭子鱼、虾和天鹅发现路上有一辆 车装满 了好吃的东西 , 于是就想把车子从路上拖下来 , 三个家伙一齐铆足了劲 , 使出了平生的力气一起拖车 , 可是 , 无论它们怎样用力 , 小车还是在老地方一步 也 不 动 . 原来 , 天鹅使劲往天上提 , 虾一步步向后倒拖 , 梭子鱼又朝着池塘拉去 . 同学们 , 你知道为什么车会一动不动吗 ? 激趣诱思 知识点拨 一、空间向量的定义及相关概念 1 . 定义 在空间 , 我们把具有 　　　　 和 　　　　 的量叫做空间向量 , 空间向量的大小叫做空间向量的 　　　　　　 .   2 . 空间向量及其模的表示方法 空间向量用字母 a , b , c , … 表示 . 若向量 a 的起点是 A , 终点是 B , 则向量 a 也可以记作 　　　　 , 其模记 大小 方向 长度或 模 激趣诱思 知识点拨 3 . 空间向量的相关 概念 平行或 重合 激趣诱思 知识点拨 名师点析 1 . 空间向量只有大小和方向 , 同向且等长的有向线段表示同一向量或相等向量 , 即向量可以在空间中平移 . 2 . 我们规定 : 零向量与任意向量平行 , 即对于任意向量 a , 都有 0 ∥ a . 激趣诱思 知识点拨 微思考 涉及空间两个向量的问题 , 平面向量中的有关结论是否仍然适用 ? 提示 : 适用 . 激趣诱思 知识点拨 微练习 ( 多选题 ) 下列命题正确的是 ( 　　 ) A. 若向量 a 与 b 的方向相反 , 则称向量 a 与 b 为相反向量 B. 零向量没有方向 C. 若 a 是单位向量 , 则 | a |= 1 D. 若向量 m , n , p 满足 m = n , n = p , 则一定有 m = p 答案 : C D 　 解析 : 单位向量是指模等于 1 的向量 , 所以若 a 是单位向量 , 则必有 | a |= 1, 即选项 C 正确 ; 由向量相等的定义 , 知 m 与 p 方向相同 , 模相等 , 故一定有 m = p , 选项 D 正确 . 激趣诱思 知识点拨 二、空间向量的线性 运算 激趣诱思 知识点拨 微练习 1 已知空间四边形 ABCD 中 , A. a+b-c 　　　　 B. c-a-b C. c+a-b D. c+a+b 答案 : B 激趣诱思 知识点拨 微练习 2 已知空间四边形 ABCD , M , G 分别是 BC , CD 的中点 , 连接 AM , AG , MG , 答案 : A 激趣诱思 知识点拨 三、共线向量与共面向量 1 . 互相平行或 重合 同一个 平面 a = λ b p =x a +y b 激趣诱思 知识点拨 激趣诱思 知识点拨 2 . 如图 , O 是直线 l 上一点 , 在直线 l 上取非零向量 a , 则对于直线 l 上任意一点 P , 由数乘向量的定义及向量共线的充要条件可知 , 存在实数 λ , 使得 = λ a . 我们把与向量 a 平行的非零向量称为直线 l 的 　　　　　 . 这样 , 直线 l 上任意一点都可以由直线 l 上的一点和它的方向向量表示 , 也就是说 , 直线可以由其上一点和它的方向向量确定 .   方向向量 激趣诱思 知识点拨 名师点析 共线向量的特点及三点共线的充要条件 (1) 共线向量不具有传递性 因为零向量 0 = 0 · a , 所以零向量和空间任一向量 a 是共线 ( 平行 ) 向量 , 这一性质使共线向量不具有传递性 , 即若 a ∥ b , b ∥ c , 则 a ∥ c 不一定成立 . 因为当 b=0 时 , a ∥ 0 , 0 ∥ c , 但 a 与 c 不一定共线 . (2) 空间三点共线的充要条件 激趣诱思 知识点拨 微练习 1 满足下列条件 , 能说明空间不重合的 A , B , C 三点共线的是 ( 　　 ) 答案 : C 激趣诱思 知识点拨 微练习 2 对于空间的任意三个向量 a , b ,2 a-b , 它们一定是 ( 　　 ) A. 共面向量 B. 共线向量 C. 不共面向量 D. 既不共线也不共面的向量 答案 : A 解析 : 因为 2 a-b= 2· a+ ( - 1)· b , 激趣诱思 知识点拨 微判断 判断下列命题是否正确 . ( 正确的打 “ √ ”, 错误的打 “ × ”) (1) 若 a 与 b 共线 , b 与 c 共线 , 则 a 与 c 共线 . ( 　　 ) (2) 若向量 a , b , c 共面 , 即表示这三个向量的有向线段所在的直线共面 . ( 　　 ) (3) 若 a ∥ b , 则存在唯一的实数 λ , 使 a = λ b . ( 　　 ) 答案 : (1) × 　 (2) × 　 (3 ) × 探究一 探究二 探究三 探究四 素养形成 当堂检测 空间向量及相关概念的 理解 解析 : ① 错误 , 在同一条直线上的单位向量 , 方向可能相同 , 也可能相反 , 故它们不一定相等 ; ② 正确 , 零向量的模等于 0, 模等于 0 的向量只有零向量 ; ② ③ 探究一 探究二 探究三 探究四 素养形成 当堂检测 反思感悟 空间向量概念的辨析 (1) 向量的两个要素是大小与方向 , 两者缺一不可 ; (2) 单位向量的方向虽然不一定相同 , 但长度一定为 1; (3) 两个向量的模相等 , 即它们的长度相等 , 但方向不确定 , 即两个向量 ( 非零向量 ) 的模相等是两个向量相等的必要不充分条件 ; (4) 由于方向不能比较大小 , 因此 “ 大于 ”“ 小于 ” 对向量来说是没有意义的 , 但向量的模是可以比较大小的 . 探究一 探究二 探究三 探究四 素养形成 当堂检测 变式训练 1 下列说法正确的是 ( 　　 ) A. 若 | a |=| b | , 则 a , b 的长度相同 , 方向相同或相反 B. 若向量 a 是向量 b 的相反向量 , 则 | a |=| b | C. 两个向量相等 , 若它们的起点相同 , 则其终点不一定相同 D. 若 | a |>| b | , | b |>| c | , 则 a > c 答案 : B 　 解析 : 两个向量是相反向量时 , 它们的模必相等 , 故选项 B 正确 . 探究一 探究二 探究三 探究四 素养形成 当堂检测 空间向量的线性 运算 思路分析 根据数乘向量及三角形法则 , 平行四边形法则求解 . 探究一 探究二 探究三 探究四 素养形成 当堂检测 反思感悟 空间向量线性运算的技巧和思路 (1) 空间向量加法、减法运算的两个技巧 ① 巧用相反向量 : 向量加减法的三角形法则是解决空间向量加法、减法运算的关键 , 灵活应用相反向量可使有关向量首尾相接 , 从而便于运算 . ② 巧用平移 : 利用三角形法则和平行四边形法则进行向量的加法、减法运算时 , 务必要注意和向量、差向量的方向 , 必要时可采用空间向量的自由平移获得更准确的结果 . 探究一 探究二 探究三 探究四 素养形成 当堂检测 (2) 化简空间向量的常用思路 ① 分组 : 合理分组 , 以便灵活运用三角形法则、平行四边形法则进行化简 . ② 多边形法则 : 在空间向量的加法运算中 , 若是多个向量求和 , 还可利用多边形法则 , 若干个向量的和可以将其转化为首尾相接的向量求和 . ③ 走边路 : 灵活运用空间向量的加法、减法法则 , 尽量走边路 ( 即沿几何体的边选择途径 ) . 探究一 探究二 探究三 探究四 素养形成 当堂检测 探究一 探究二 探究三 探究四 素养形成 当堂检测 探究一 探究二 探究三 探究四 素养形成 当堂检测 空间共线向量定理及其 应用 探究一 探究二 探究三 探究四 素养形成 当堂检测 探究一 探究二 探究三 探究四 素养形成 当堂检测 反思感悟 利用空间向量共线定理可解决的主要问题 1 . 判断两向量是否共线 : 判断两向量 a , b ( b ≠ 0 ) 是否共线 , 即判断是否存在实数 λ , 使 a = λ b . 2 . 求解参数 : 已知两非零向量共线 , 可求其中参数的值 , 即利用 “ 若 a ∥ b , 则 a = λ b ( λ ∈ R )” . 3 . 判断或证明空间中的三点 ( 如 P , A , B ) 是否共线 : 探究一 探究二 探究三 探究四 素养形成 当堂检测 解 : ∵ M , N 分别是 AC , BF 的中点 , 且 四边形 ABCD , ABEF 都是平行四边形 , 探究一 探究二 探究三 探究四 素养形成 当堂检测 空间共面向量定理及其 应用 (2) 判断点 M 是否在平面 ABC 内 . 探究一 探究二 探究三 探究四 素养形成 当堂检测 探究一 探究二 探究三 探究四 素养形成 当堂检测 反思感悟 证明共面问题的基本方法 (1) 证明两个空间向量共面时 , 可以利用共面向量的充要条件 , 也可直接利用共面向量的定义 , 通过线面平行、直线在平面内等进行证明 . (2) 证明空间四点 P , M , A , B 共面时 , 可以通过以下几种条件进行证明 . 探究一 探究二 探究三 探究四 素养形成 当堂检测 变式训练 4 已知 A , B , C 三点不共线 , 点 O 是平面 ABC 外的任意一点 , 若点 P 分别满足下列关系 : 试判断点 P 是否与点 A , B , C 共面 . 探究一 探究二 探究三 探究四 素养形成 当堂检测 探究一 探究二 探究三 探究四 素养形成 当堂检测 一题多变 —— 空间向量的加法、减法 运算 探究一 探究二 探究三 探究四 素养形成 当堂检测 探究一 探究二 探究三 探究四 素养形成 当堂检测 解 : (1) 根据六棱柱的性质知四边形 BB 1 C 1 C , DD 1 E 1 E 都是平行四边形 , 探究一 探究二 探究三 探究四 素养形成 当堂检测 方法总结 在进行减法运算时 , 可将减去一个向量转化为加上这个向量的相反向量 , 而在进行加法运算时 , 首先考虑这两个向量在哪个平面内 , 然后与平面向量求和一样 , 运用向量运算的平行四边形法则、三角形法则及多边形法则来求 . 探究一 探究二 探究三 探究四 素养形成 当堂检测 1 . “ 两个非零空间向量的模相等 ” 是 “ 两个空间向量相等 ” 的 ( 　　 ) A. 充分不必要条件 B . 必要不充分条件 C. 充要条件 D . 既不充分也不必要条件 2 . 在平行六面体 ABCD-A‘B’C‘D’ 中 , 与 向量 相等 的向量共有 ( 　　 ) A.1 个 B.2 个 C.3 个 D.4 个 答案 : B 　 解析 : 两个向量相等是指两个向量的模相等并且方向相同 , 因此 “ 两个非零向量的模相等 ” 是 “ 两个向量相等 ” 的必要不充分条件 . 答案 : C 　 探究一 探究二 探究三 探究四 素养形成 当堂检测 3 . 如 图 , 在平行六面体 ABCD-A 1 B 1 C 1 D 1 中 , 点 M 为 A 1 C 1 与 B 1 D 1 的交 答案 : B 　 探究一 探究二 探究三 探究四 素养形成 当堂检测 4 . 下列条件使点 M 与点 A , B , C 一定共面的是 ( 　　 ) 答案 : D 　 解析 : 根据共面向量定理知 A,B,C 均错 , 只有 D 能使其一定共面 . 探究一 探究二 探究三 探究四 素养形成 当堂检测 5 . 如 图所示 , 已知矩形 ABCD , P 为平面 ABCD 外一点 , 且 PA ⊥ 平面 ABCD , M , N 分别为 PC , PD 上的点 , 且 PM ∶ MC= 2 ∶ 1, N 为 PD 中点 , 探究一 探究二 探究三 探究四 素养形成 当堂检测 解 : 如 图 , 在 PD 上取一点 F , 使 PF ∶ FD= 2 ∶ 1, 连接 MF ,