2020高中数学 第二章 数列2.2 直线与平面平行 4页

‎2.2　直线与平面平行 ‎【基本知识】 ‎ 知识点一　空间中直线与平面的位置关系 直线与平面的位置关系 位置关系 直线在平面内 直线在平面外 直线与平面相交 直线与平面平行 公共点 ‎ ‎ 公共点 ‎ ‎ 公共点 ‎ ‎ 公共点 符号表示 图形表示 知识点二　直线与平面平行的判定 表示 定理 图形 文字 符号 直线与平面平行的判定定理 如果不在一个平面内的一条直线和平面内的 ，那么这条直线和这个平面平行 ‎ ‎ 知识点三　直线与平面平行的性质定理 文字语言 如果一条直线和一个平面平行，经过这条直线的平面和这个平面相交，那么这条直线就和两个平面的交线 .‎ 符号语言 ‎ ‎ 图形语言 作用 线面平行线线平行 ‎【归纳·升华·领悟】‎ ‎1.利用公共点的个数也可以理解直线与平面的位置关系 ‎（1）当直线与平面无公共点时，直线与平面平行.‎ ‎（2）当直线与平面有一个公共点时，直线与平面相交.‎ ‎（3）当直线与平面有两个公共点时，它们就有无数个公共点，这时直线在平面内.‎ ‎2.直线与平面平行的判定定理在使用时要注意线在面外，这一条件易被忽视.‎ ‎3.对线面平行性质定理的理解 ‎（1）如果直线平面，在平面内，除了与直线 4‎ 平行的直线外，其余的任一直线都与是异面直线.‎ ‎（2）线面平行的性质定理的条件有三：①直线与平面平行，即；②平面、相交于一条直线，即；③直线在平面内，即.三个条件缺一不可.‎ ‎【典型例题】‎ 考点一　直线与平面的位置关系 例1.下列命题中，，，表示直线，表示平面.‎ ‎①若，，且，不相交，则.‎ ‎②若，，，，且和，均不相交，则.‎ ‎③若点，则过点可以作无数个平面与平行.‎ ‎④若与内的无数条直线不相交，则.‎ 其中正确的命题有 （把你认为正确的序号都填上）.‎ 考点二　直线和平面平行的判定 例2.如图，是平行四边形平面外一点，，分别是，上的点，且.‎ 求证：平面.‎ 考点三　线面平行的性质及应用 例3.如图所示，已知三棱锥被一平面所截，截面为，求证： 平面.‎ 4‎ ‎【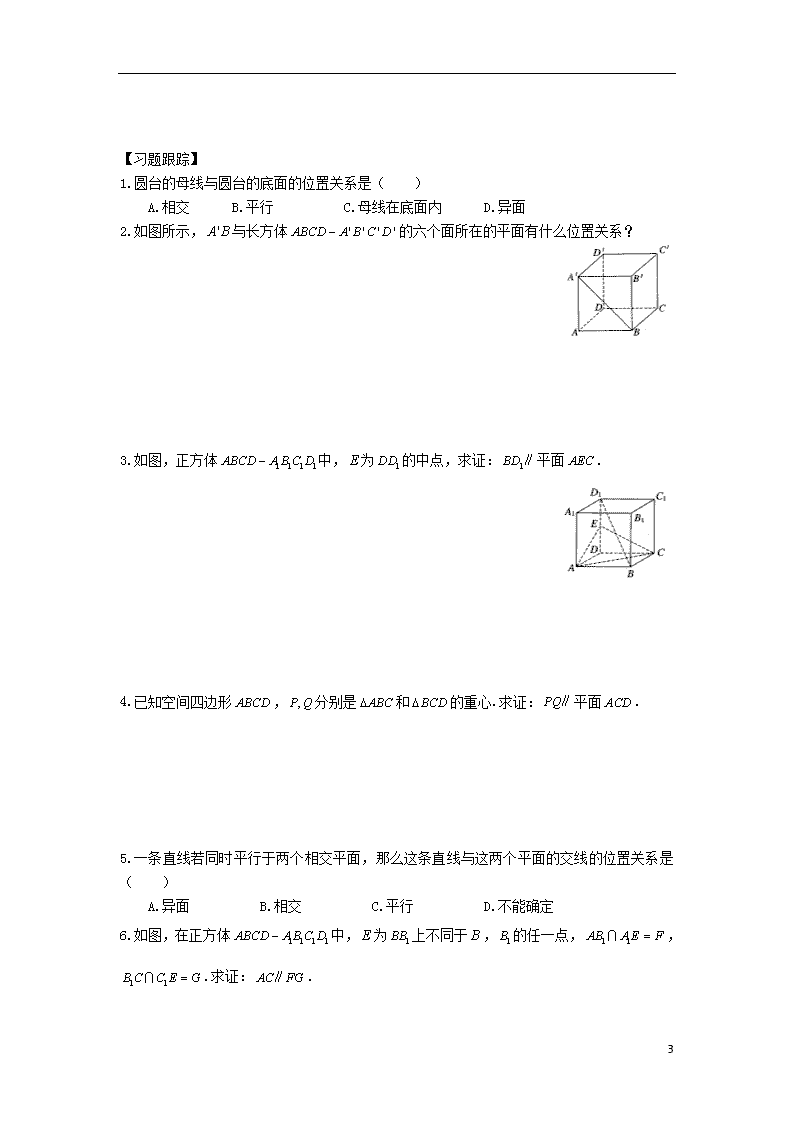习题跟踪】‎ ‎1.圆台的母线与圆台的底面的位置关系是（　　）‎ A.相交 B.平行 C.母线在底面内 D.异面 ‎2.如图所示，与长方体的六个面所在的平面有什么位置关系？‎ ‎3.如图，正方体中，为的中点，求证：平面.‎ ‎4.已知空间四边形，分别是和的重心.求证：平面.‎ ‎5.一条直线若同时平行于两个相交平面，那么这条直线与这两个平面的交线的位置关系是（　　）‎ A.异面 B.相交 C.平行 D.不能确定 ‎6.如图，在正方体中，为上不同于，的任一点，，.求证：.‎ 4‎ ‎【方法·规律·小结】‎ ‎1.利用直线与平面平行判定定理来证明线面平行，关键是寻找面内与已知直线平行的直线，常利用平行四边形、三角形中位线、平行公理等.‎ ‎2.利用线面平行的性质定理解题步骤 ‎（1）确定（或寻找）一条直线平行于一个平面；‎ ‎（2）确定（或寻找）过这条直线且与这个平行平面相交的平面；‎ ‎（3）确定交线，由性质定理得出结论.‎ 4‎