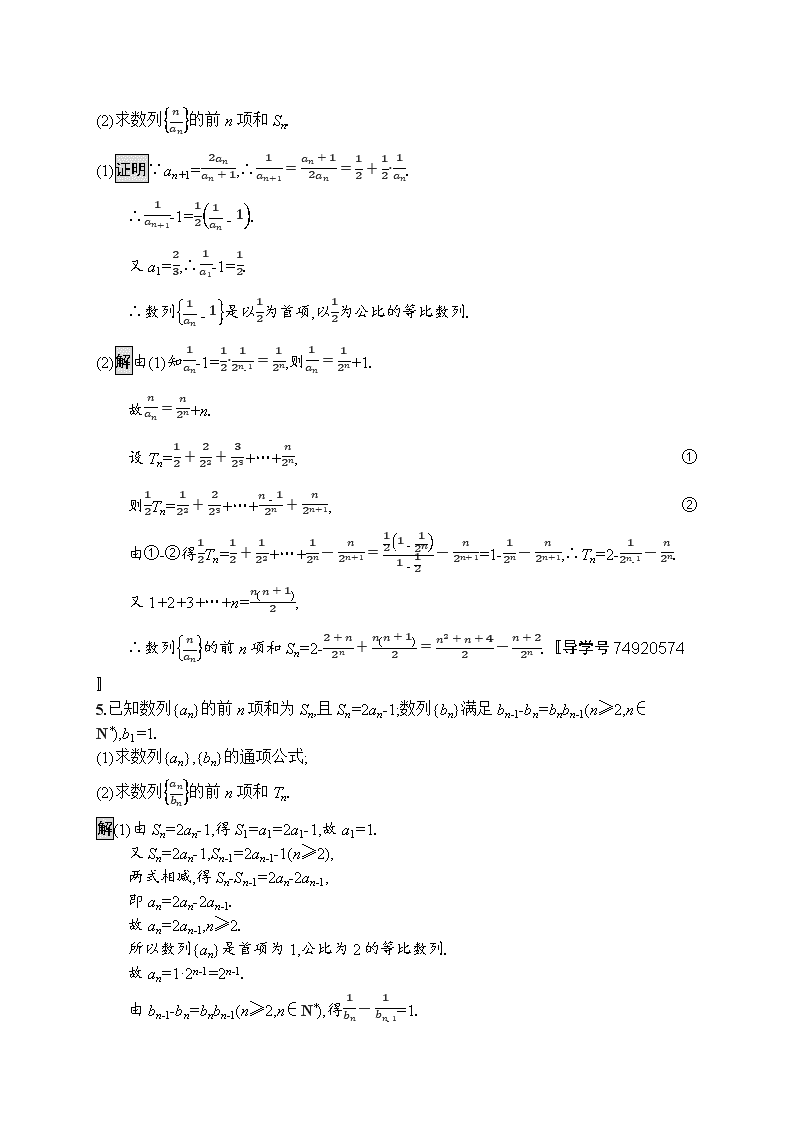高考数学专题复习练习：高考大题专项练三 6页

高考大题专项练三　高考中的数列 ‎　高考大题专项练第6页　 ‎ ‎1.(2016河北唐山高三检测)已知等差数列{an}的前n项和为Sn,公差d≠0,且S3+S5=50,a1,a4,a13成等比数列.‎ ‎(1)求数列{an}的通项公式;‎ ‎(2)设bnan是首项为1,公比为3的等比数列,求数列{bn}的前n项和Tn.‎ 解(1)依题意得,‎‎3a‎1‎+‎3×2‎‎2‎d+5a‎1‎+‎4×5‎‎2‎d=50,‎‎(a‎1‎+3d‎)‎‎2‎=a‎1‎(a‎1‎+12d),‎ 解得a‎1‎‎=3,‎d=2.‎ 故an=a1+(n-1)d=3+2(n-1)=2n+1,‎ 即an=2n+1.‎ ‎(2)由题意可知bnan=3n-1,‎ 则bn=an·3n-1=(2n+1)·3n-1.‎ 故Tn=3+5×3+7×32+…+(2n+1)·3n-1,①‎ ‎3Tn=3×3+5×32+7×33+…+(2n-1)·3n-1+(2n+1)·3n,②‎ ‎①-②得 ‎-2Tn=3+2×3+2×32+…+2·3n-1-(2n+1)3n ‎=3+2·‎3(1-‎3‎n-1‎)‎‎1-3‎-(2n+1)3n=-2n·3n,‎ 因此,Tn=n·3n.〚导学号74920571〛‎ ‎2.(2016河北衡水中学考前仿真二)设数列{an}的前n项和为Sn,已知a1=3,Sn+1=3Sn+3.‎ ‎(1)求数列{an}的通项公式;‎ ‎(2)若bn=nan+1‎‎-‎an,求数列{bn}的前n项和Tn.‎ 解(1)(方法一)∵Sn+1=3Sn+3,‎ ‎∴Sn+1+‎3‎‎2‎=3Sn‎+‎‎3‎‎2‎.‎ ‎∴Sn+‎3‎‎2‎‎=‎S‎1‎‎+‎‎3‎‎2‎3n-1=‎9‎‎2‎×3n-1=‎3‎n+1‎‎2‎.‎ ‎∴当n≥2时,an=Sn-Sn-1=‎3‎n+1‎‎2‎‎-‎‎3‎n‎2‎=3n,a1也适合.‎ ‎∴an=3n.‎ ‎(方法二)由Sn+1=3Sn+3(n∈N*),‎ 可知当n≥2时,Sn=3Sn-1+3,‎ 两式相减,得an+1=3an(n≥2).‎ 又a1=3,代入Sn+1=3Sn+3得a2=9,故an=3n.‎ ‎(2)∵bn=nan+1‎‎-‎an‎=n‎3‎n+1‎‎-‎‎3‎n=‎1‎‎2‎·‎n‎3‎n,‎ ‎∴Tn=‎1‎‎2‎‎1‎‎3‎‎+‎2‎‎3‎‎2‎+‎3‎‎3‎‎3‎+…+‎n‎3‎n,①‎ ‎∴‎1‎‎3‎Tn=‎1‎‎2‎‎1‎‎3‎‎2‎‎+‎2‎‎3‎‎3‎+‎3‎‎3‎‎4‎+…+n-1‎‎3‎n+‎n‎3‎n+1‎,②‎ 由①-②,得‎2‎‎3‎Tn=‎1‎‎2‎‎1‎‎3‎‎+‎1‎‎3‎‎2‎+‎1‎‎3‎‎3‎+‎1‎‎3‎‎4‎+…+‎1‎‎3‎n-‎n‎3‎n+1‎,‎ 解得Tn=‎3‎‎8‎‎-‎‎2n+3‎‎8·‎‎3‎n.〚导学号74920572〛‎ ‎3.(2016四川,文19)已知数列{an}的首项为1,Sn为数列{an}的前n项和,Sn+1=qSn+1,其中q>0,n∈N*.‎ ‎(1)若a2,a3,a2+a3成等差数列,求数列{an}的通项公式;‎ ‎(2)设双曲线x2-y‎2‎an‎2‎=1的离心率为en,且e2=2,求e‎1‎‎2‎‎+‎e‎2‎‎2‎+…+en‎2‎.‎ 解(1)由已知,Sn+1=qSn+1,Sn+2=qSn+1+1,‎ 两式相减得到an+2=qan+1,n≥1.‎ 又由S2=qS1+1得到a2=qa1,‎ 故an+1=qan对所有n≥1都成立.‎ 所以,数列{an}是首项为1,公比为q的等比数列.‎ 从而an=qn-1.‎ 由a2,a3,a2+a3成等差数列,可得2a3=a2+a2+a3.‎ 所以a3=2a2,故q=2.所以an=2n-1.‎ ‎(2)由(1)可知,an=qn-1.‎ 所以双曲线x2-y‎2‎an‎2‎=1的离心率en=‎1+‎an‎2‎‎=‎‎1+‎q‎2(n-1)‎.‎ 由e2=‎1+‎q‎2‎=2,解得q=‎3‎.‎ 所以e‎1‎‎2‎‎+‎e‎2‎‎2‎+…+‎en‎2‎ ‎=(1+1)+(1+q2)+…+[1+q2(n-1)]‎ ‎=n+[1+q2+…+q2(n-1)]‎ ‎=n+q‎2n-1‎q‎2‎‎-1‎=n+‎1‎‎2‎(3n-1).〚导学号74920573〛‎ ‎4.(2016山西晋中5月高三质检)已知数列{an}的首项a1=‎2‎‎3‎,an+1=‎2‎anan‎+1‎(n∈N*).‎ ‎(1)求证:数列‎1‎an‎-1‎是等比数列;‎ ‎(2)求数列nan的前n项和Sn.‎ ‎(1)证明∵an+1=‎2‎anan‎+1‎,∴‎1‎an+1‎‎=an‎+1‎‎2‎an=‎1‎‎2‎+‎1‎‎2‎·‎‎1‎an.‎ ‎∴‎1‎an+1‎-1=‎1‎‎2‎‎1‎an‎-1‎.‎ 又a1=‎2‎‎3‎,∴‎1‎a‎1‎-1=‎1‎‎2‎.‎ ‎∴数列‎1‎an‎-1‎是以‎1‎‎2‎为首项,以‎1‎‎2‎为公比的等比数列.‎ ‎(2)解由(1)知‎1‎an-1=‎1‎‎2‎‎·‎1‎‎2‎n-1‎=‎‎1‎‎2‎n,则‎1‎an‎=‎‎1‎‎2‎n+1.‎ 故nan‎=‎n‎2‎n+n.‎ 设Tn=‎1‎‎2‎‎+‎2‎‎2‎‎2‎+‎‎3‎‎2‎‎3‎+…+n‎2‎n,①‎ 则‎1‎‎2‎Tn=‎1‎‎2‎‎2‎‎+‎‎2‎‎2‎‎3‎+…+n-1‎‎2‎n‎+‎n‎2‎n+1‎,②‎ 由①-②得‎1‎‎2‎Tn=‎1‎‎2‎‎+‎‎1‎‎2‎‎2‎+…+‎1‎‎2‎n‎-n‎2‎n+1‎=‎1‎‎2‎‎1-‎‎1‎‎2‎n‎1-‎‎1‎‎2‎-‎n‎2‎n+1‎=1-‎1‎‎2‎n‎-‎n‎2‎n+1‎,∴Tn=2-‎1‎‎2‎n-1‎‎-‎n‎2‎n.‎ 又1+2+3+…+n=n(n+1)‎‎2‎,‎ ‎∴数列nan的前n项和Sn=2-‎2+n‎2‎n‎+n(n+1)‎‎2‎=n‎2‎‎+n+4‎‎2‎-‎n+2‎‎2‎n.〚导学号74920574〛‎ ‎5.已知数列{an}的前n项和为Sn,且Sn=2an-1;数列{bn}满足bn-1-bn=bnbn-1(n≥2,n∈N*),b1=1.‎ ‎(1)求数列{an},{bn}的通项公式;‎ ‎(2)求数列anbn的前n项和Tn.‎ 解(1)由Sn=2an-1,得S1=a1=2a1-1,故a1=1.‎ 又Sn=2an-1,Sn-1=2an-1-1(n≥2),‎ 两式相减,得Sn-Sn-1=2an-2an-1,‎ 即an=2an-2an-1.‎ 故an=2an-1,n≥2.‎ 所以数列{an}是首项为1,公比为2的等比数列.‎ 故an=1·2n-1=2n-1.‎ 由bn-1-bn=bnbn-1(n≥2,n∈N*),得‎1‎bn‎-‎‎1‎bn-1‎=1.‎ 又b1=1,∴数列‎1‎bn是首项为1,公差为1的等差数列.‎ ‎∴‎1‎bn=1+(n-1)·1=n.‎ ‎∴bn=‎1‎n.‎ ‎(2)由(1)得anbn=n·2n-1.‎ ‎∴Tn=1·20+2·21+…+n·2n-1,‎ ‎∴2Tn=1·21+2·22+…+n·2n.‎ 两式相减,得-Tn=1+21+…+2n-1-n·2n ‎=‎1-‎‎2‎n‎1-2‎-n·2n=-1+2n-n·2n.‎ ‎∴Tn=(n-1)·2n+1.〚导学号74920575〛‎ ‎6.设Sn为等差数列{an}的前n项和,已知S3=a7,a8-2a3=3.‎ ‎(1)求an;‎ ‎(2)设bn=‎1‎Sn,数列{bn}的前n项和为Tn,求证:Tn>‎3‎‎4‎‎-‎‎1‎n+1‎(n∈N*).‎ ‎(1)解设等差数列{an}的公差为d,‎ 由题意得‎3a‎1‎+3d=a‎1‎+6d,‎‎(a‎1‎+7d)-2(a‎1‎+2d)=3,‎解得a‎1‎‎=3,‎d=2.‎ 故an=a1+(n-1)d=2n+1.‎ ‎(2)证明∵a1=3,d=2,‎ ‎∴Sn=na1+n(n-1)‎‎2‎d=n(n+2).‎ ‎∴bn=‎1‎n(n+2)‎‎=‎‎1‎‎2‎‎1‎n‎-‎‎1‎n+2‎.‎ ‎∴Tn=b1+b2+…+bn-1+bn ‎=‎‎1‎‎2‎‎1-‎‎1‎‎3‎‎+‎1‎‎2‎‎-‎‎1‎‎4‎+…+‎1‎n-1‎‎-‎‎1‎n+1‎+‎‎1‎n‎-‎‎1‎n+2‎ ‎=‎‎1‎‎2‎‎1+‎1‎‎2‎-‎1‎n+1‎-‎‎1‎n+2‎ ‎>‎1‎‎2‎‎1+‎1‎‎2‎-‎1‎n+1‎-‎‎1‎n+1‎‎=‎3‎‎4‎-‎‎1‎n+1‎,‎ 故Tn>‎3‎‎4‎‎-‎‎1‎n+1‎.〚导学号74920576〛‎ ‎7.已知正项数列{an}的首项a1=1,前n项和Sn满足an=Sn‎+‎Sn-1‎(n≥2).‎ ‎(1)求证:{Sn}为等差数列,并求数列{an}的通项公式;‎ ‎(2)记数列‎1‎anan+1‎的前n项和为Tn,若对任意的n∈N*,不等式4Tn