2020高中数学 第1章 点、直线、面的位置关系12 面面垂直的性质学案 苏教版必修2 5页

面面垂直的性质 一、考点突破 知识点 课标要求 题型 说明 面面垂直的性质 ‎1. 理解面面垂直性质定理的含义；‎ ‎2. 能运用性质定理证明相关问题；‎ ‎3. 理解并掌握空间“平行”与“垂直”之间的相互转化。‎ 选择题 填空题 解答题 垂直关系是高考的重点内容，同学们要多练习多思考，认真掌握。‎ 其中二面角的平面角是难点。‎ 二、重难点提示 重点：平面和平面垂直的性质定理及二面角的平面角问题。‎ 难点：平面和平面垂直的性质定理的应用及二面角的平面角问题 考点一：平面与平面垂直的性质 ‎1. 平面与平面垂直的性质定理 文字语言 如果两个平面互相垂直，那么在一个平面内垂直于它们交线的直线垂直于另一个平面。‎ 符号语言 α⊥β，α∩β＝l，a⊂α，a⊥l⇒a⊥β 图形语言 简记为：面面垂直⇒线面垂直 ‎2 .平面与平面垂直的其他性质 ‎（1）如果两个平面垂直，那么经过第一个平面内一点垂直于第二个平面的直线在第一个平面内。其图形语言和符号语言如下：‎ ‎（2）如果两个平面垂直，那么与其中一个平面平行的平面垂直于另一个平面，‎ 即∥‎ ‎（3）如果两个相交平面都垂直于第三个平面，那么它们的交线垂直于第三个平面，即 ‎（4）三个两两垂直的平面的交线两两垂直，即 5‎ 考点二：二面角的求法 ‎【规律总结】‎ 作二面角的一般方法 ‎（1）定义法：在二面角的棱上找一个特殊点，在两个半平面内分别作垂直于棱的射线，如图①，则∠AOB为二面角α－l－β的平面角。‎ 由定义法作出二面角的平面角，若已知二面角的两个面是特殊的三角形（如以棱为公共边的两个等腰三角形），这时可以选取棱上的特殊点，如公共底边的中点或公共底边上高的垂足，从特殊点出发根据定义作出二面角的平面角。‎ ‎（2）垂面法：过棱上一点作棱的垂直平面，该平面与二面角的两个半平面产生交线，这两条交线所成的角，即为二面角的平面角，如图②，∠AOB为二面角α－l－β的平面角。‎ ‎（3）线面垂直法：过二面角的一个面内异于棱上的A点向另一个平面作垂线，垂足为B，由点B向二面角的棱作垂线，垂足为O，连接AO，则∠AOB为二面角的平面角或其补角，如图③，∠AOB为二面角α－l－β的平面角，这种方法是求二面角大小最常用的方法。‎ ‎（4）射影面积法 设二面角为，过作于点，过作于点，连接，则是二面角的平面角，于是。‎ ‎【要点诠释】‎ 对于特殊图形，不易作出二面角的平面角时，可用上述公式计算。‎ ‎【规律总结】‎ 求二面角同求异面直线所成的角及斜线与平面所成的角一样，步骤如下：‎ 5‎ 简称为“一作二证三算四答”。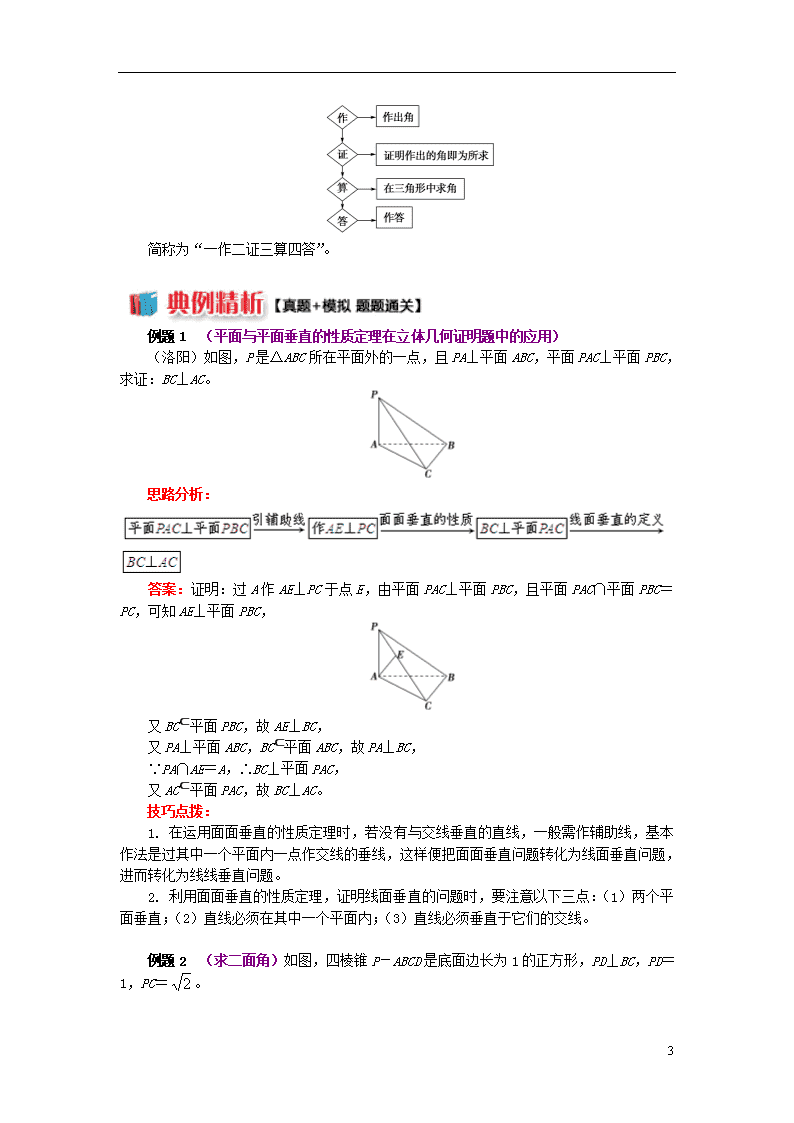‎ 例题1 （平面与平面垂直的性质定理在立体几何证明题中的应用）‎ ‎（洛阳）如图，P是△ABC所在平面外的一点，且PA⊥平面ABC，平面PAC⊥平面PBC，求证：BC⊥AC。‎ 思路分析：‎ ‎ ‎ 答案：证明：过A作AE⊥PC于点E，由平面PAC⊥平面PBC，且平面PAC∩平面PBC＝PC，可知AE⊥平面PBC，‎ 又BC⊂平面PBC，故AE⊥BC，‎ 又PA⊥平面ABC，BC⊂平面ABC，故PA⊥BC，‎ ‎∵PA∩AE＝A，∴BC⊥平面PAC，‎ 又AC⊂平面PAC，故BC⊥AC。‎ 技巧点拨：‎ ‎1. 在运用面面垂直的性质定理时，若没有与交线垂直的直线，一般需作辅助线，基本作法是过其中一个平面内一点作交线的垂线，这样便把面面垂直问题转化为线面垂直问题，进而转化为线线垂直问题。‎ ‎2. 利用面面垂直的性质定理，证明线面垂直的问题时，要注意以下三点：（1）两个平面垂直；（2）直线必须在其中一个平面内；（3）直线必须垂直于它们的交线。‎ 例题2 （求二面角）如图，四棱锥P－ABCD是底面边长为1的正方形，PD⊥BC，PD＝1，PC＝。‎ 5‎ ‎（1）求证：PD⊥面ABCD；‎ ‎（2）求二面角A－PB－D的大小。‎ 思路分析：（1） 利用线面垂直的判定定理；（2） 利用线面垂直法找出二面角的平面角，在三角形中计算角的大小。‎ 答案：（1）证明：∵PD＝DC＝1，PC＝，‎ ‎∴△PDC是直角三角形，即PD⊥CD，‎ 又∵PD⊥BC，BC∩CD＝C，‎ ‎∴PD⊥面ABCD；‎ ‎（2）解：连接BD，设BD交AC于点O，过O作OE⊥PB于点E，连接AE，‎ ‎∵PD⊥面ABCD，∴AO⊥PD，‎ 又∵AO⊥BD，∴AO⊥面PDB，‎ ‎∴AO⊥PB，‎ 又∵OE⊥PB，OE∩AO＝O，‎ ‎∴PB⊥平面AEO，从而PB⊥EO，‎ 故∠AEO就是二面角A－PB－D的平面角，‎ ‎∵PD⊥面ABCD，∴PD⊥BD，‎ ‎∴在Rt△PDB中，PB＝＝，‎ 又∵，∴OE＝，‎ ‎∴tan∠AEO＝＝，∴∠AEO＝60°，‎ 故二面角A－PB－D的大小为60°。‎ 技巧点拨：‎ 用线面垂直法作出二面角是最常用的找平面角的方法，关键是找到线面垂直关系。‎ 5‎ 垂面法求二面角的平面角 ‎【满分训练】如果二面角α－l－β的平面角是锐角，点P到α，β和棱l的距离分别为2、4和4，求二面角的大小。‎ 思路分析：点P可能在二面角α－l－β内部，也可能在外部，应分别处理。‎ 答案：如图（1）是点P在二面角α－l－β的内部的情况。图（2）是点P在二面角α－l－β的外部的情况。‎ ‎∵PA⊥α，∴PA⊥l，‎ ‎∵AC⊥l，∴l⊥平面PAC，‎ 同理，l⊥平面PBC，而平面PAC∩平面PBC＝PC，‎ ‎∴平面PAC与平面PBC应重合，‎ 即A、C、B、P在同一平面内，则∠ACB是二面角α－l－β的平面角，‎ 在Rt△APC中，sin∠ACP＝，‎ ‎∴∠ACP＝30°，‎ 在Rt△BPC中，sin∠BCP＝，‎ ‎∴∠BCP＝45°，‎ 故∠ACB＝30°＋45°＝75°或∠ACB＝45°－30°＝15°。‎ 即二面角α－l－β的大小为75°或15°。‎ 技巧点拨：‎ 本题主要考查求二面角的另一种方法“垂面法”，所谓“垂面法”即过棱上一点作棱的垂直平面，该平面与二面角的两个半平面相交产生两条射线，这两条射线所成的角即为二面角的平面角。‎ 5‎