2020高中数学 第2章 直线的方程3 两条直线的平行与垂直学案 苏教版必修2 3页

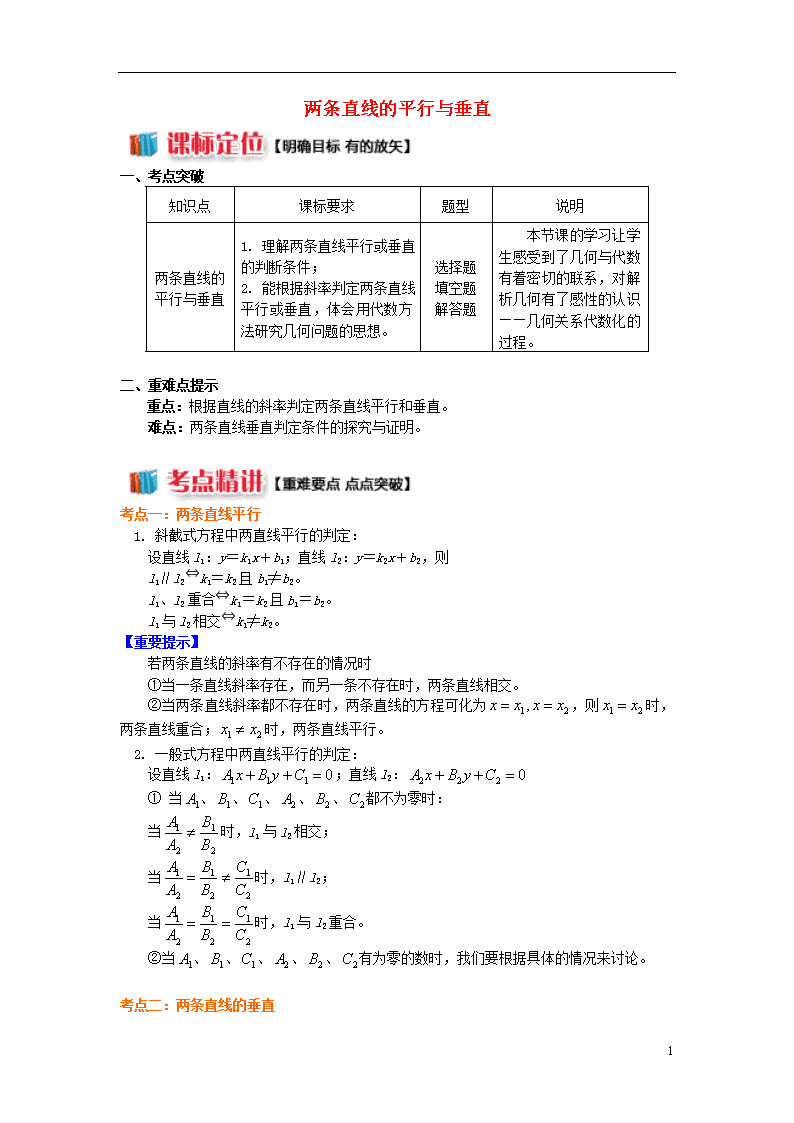
两条直线的平行与垂直 一、考点突破 知识点 课标要求 题型 说明 两条直线的平行与垂直 ‎1. 理解两条直线平行或垂直的判断条件；‎ ‎2. 能根据斜率判定两条直线平行或垂直，体会用代数方法研究几何问题的思想。‎ 选择题 填空题 解答题 本节课的学习让学生感受到了几何与代数有着密切的联系，对解析几何有了感性的认识——几何关系代数化的过程。‎ 二、重难点提示 重点：根据直线的斜率判定两条直线平行和垂直。‎ 难点：两条直线垂直判定条件的探究与证明。‎ 考点一：两条直线平行 ‎1. 斜截式方程中两直线平行的判定：‎ 设直线l1：y＝k1x＋b1；直线l2：y＝k2x＋b2，则 l1∥l2⇔k1＝k2且b1≠b2。‎ l1、l2重合⇔k1＝k2且b1＝b2。‎ l1与l2相交⇔k1≠k2。‎ ‎【重要提示】‎ 若两条直线的斜率有不存在的情况时 ‎①当一条直线斜率存在，而另一条不存在时，两条直线相交。‎ ‎②当两条直线斜率都不存在时，两条直线的方程可化为，则时，两条直线重合；时，两条直线平行。‎ ‎2. 一般式方程中两直线平行的判定：‎ 设直线l1：；直线l2：‎ ‎① 当、、、、、都不为零时：‎ 当时，l1与l2相交；‎ 当时，l1∥l2；‎ 当时，l1与l2重合。‎ ‎②当、、、、、有为零的数时，我们要根据具体的情况来讨论。‎ 考点二：两条直线的垂直 3‎ ‎1. 斜截式方程中两直线垂直的判定：‎ 设直线l1：y＝k1x＋b1；直线l2：y＝k2x＋b2，则l1⊥l2⇔k1·k2＝－1。‎ ‎2. 一般式方程中两直线垂直的判定：‎ 设直线l1：；直线l2：，则l1⊥l2⇔。‎ 例题1 （两条直线平行关系的判定）判断下列各小题中的直线l1与l2是否平行。‎ ‎（1）l1经过点A（－1，－2），B（2,1），l2经过点M（3,4），N（－1，－1）；‎ ‎（2）l1的斜率为1，l2经过点A（1,1），B（2,2）；‎ ‎（3）l1经过点A（0,1），B（1,0），l2经过点M（－1,3），N（2，0）；‎ ‎（4）l1经过点A（－3,2），B（－3,10），l2经过点M（5，－2），N（5,5）。‎ 思路分析：逐一验证是否满足k1＝k2且b1≠b2或斜率均不存在。‎ 答案：（1）k1＝＝1，k2＝＝，k1≠k2，l1与l2不平行；‎ ‎（2）k1＝1，k2＝＝1，k1＝k2，‎ ‎∴l1∥l2或l1与l2重合；‎ ‎（3）k1＝＝－1，k2＝＝－1，k1＝k2，由数形结合知，l1∥l2；‎ ‎（4）∵直线l1、l2的斜率均不存在且不重合，故l1∥l2。‎ 技巧点拨：‎ ‎1. 判定两直线平行，要“三看”：一看斜率是否存在；在斜率都存在时，二看斜率是否相等；若两直线斜率都不存在或斜率相等时，三看是否重合，若不重合则两直线平行。‎ ‎2. 判断两直线平行实质上是判断两直线的倾斜角是否相等，解题时要注意数形结合思想的应用。‎ 例题2 （两条直线垂直的判定）判断下列各小题中l1与l2是否垂直。‎ ‎（1）l1经过点A（－1，－2），B（1,2），l2经过点M（－2，－1），N（2,1）；‎ ‎（2）l1的斜率为－10，l2经过点A（10,2），B（20,3）；‎ ‎（3）l1经过点A（3,4），B（3,10），l2经过点M（－10,40），N（10,40）。‎ 思路分析：对于（1）（2），求出斜率，利用l1⊥l2⇔k1k2＝－1进行判断。对于（3）先说明l1⊥x轴，再说明l2∥x轴，从而得出l1⊥l2。‎ 答案：（1）k1＝＝2，‎ k2＝＝，k1k2＝1，∴l1与l2不垂直；‎ ‎（2）k1＝－10，k2＝＝，k1k2＝－1，∴l1⊥l2；‎ ‎（3）l1的倾斜角为90°，则l1⊥x轴，‎ k2＝＝0，则l2∥x轴，∴l1⊥l2。‎ 3‎ 技巧点拨：‎ ‎1. 解答本题的关键是计算两直线的斜率，然后看两斜率乘积是否等于－1，在（3）中有一条斜率不存在，另一条只有斜率为0时两直线才垂直。‎ ‎2. 判断两直线是否垂直的依据：在这两条直线都有斜率的前提下，只须看它们的斜率之积是否等于－1即可，但应注意当一条直线与x轴垂直，另一条直线与x轴平行时，两直线也垂直。‎ ‎　‎ 直线的平行和垂直位置关系中的分类讨论思想 ‎【满分训练】已知△ABC的顶点坐标为A（5，－1），B（1,1），C（2，m），若△ABC为直角三角形，试求m的值。‎ 思路分析：解答本题的关键是对的哪一个内角是直角分情况进行讨论，将几何图形的垂直关系转化为代数的斜率关系。‎ 答案：kAB＝＝－，kAC＝＝－，‎ kBC＝＝m－1。‎ 若AB⊥AC，则有－·＝－1，所以m＝－7。‎ 若AB⊥BC，则有－·（m－1）＝－1，所以m＝3。‎ 若AC⊥BC，则有－·（m－1）＝－1，所以m＝±2。‎ 综上可知，所求m的值为－7，±2，3。‎ 技巧点拨：‎ 注意分类讨论在直线与直线的位置关系中的应用。‎ 3‎