2015年数学理高考课件7-5 直线、平面垂直的判定及其性质 43页

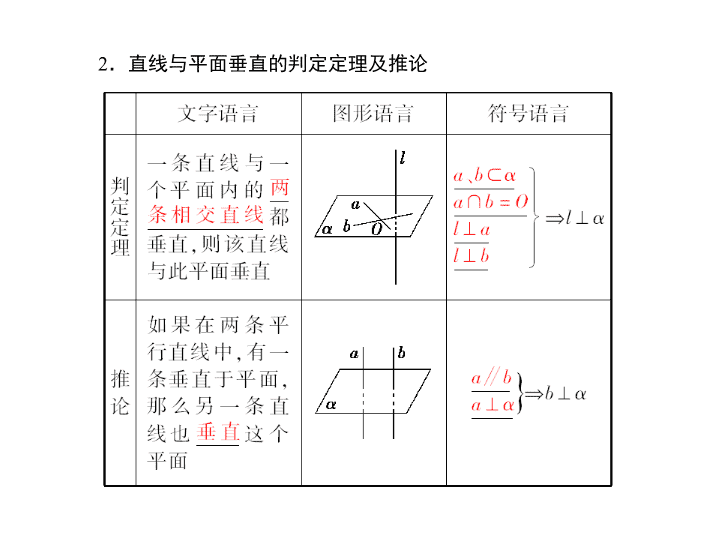
[ 最新考纲展示 ] 　 1 ． 以立体几何的定义、公理和定理为出发点，认识和理解空间中线、面垂直的有关性质与判定定理； 2. 能运用公理、定理和已获得的结论证明一些空间图形垂直关系的简单命题． 第五节　直线、平面垂直的判定及其性质 直线与平面垂直的判定及性质 1 ．直线和平面垂直的定义 直线 l 与平面 α 内的 直线都垂直，就说直线 l 与平面 α 互相垂直． 任意一条 2 ．直线与平面垂直的判定定理及推论 3. 直线与平面垂直的性质定理 ____________________[ 通关方略 ]____________________ 1 ．直线与平面垂直的定义常常逆用，即 a ⊥ α ， b ⊂ α ⇒ a ⊥ b . 2 ．若平行直线中一条垂直于平面，则另一条也垂直于该平面． 3 ．垂直于同一条直线的两个平面平行． 4 ．过一点有且只有一条直线与已知平面垂直． 5 ．过一点有且只有一个平面与已知直线垂直． 1 ．给出下列四个命题： ① 垂直于同一平面的两条直线相互平行； ② 垂直于同一平面的两个平面相互平行； ③ 若一个平面内有无数条直线与另一个平面都平行，那么这两个平面相互平行； ④ 若一条直线垂直于一个平面内的任一直线，那么这条直线垂直于这个平面． 其中真命题的个数是 ( 　　 ) A ． 1 　　　　　　　　　　 B ． 2 C ． 3 D ． 4 解析： 命题 ① ， ④ 为真，命题 ② ， ③ 为假，故选 B. 答案： B 2 ．设 l ， m ， n 为三条不同的直线， α ， β 为两个不同的平面，下列命题中正确的是 ( 　　 ) A ．若 l ⊥ α ， m ∥ β ， α ⊥ β ，则 l ⊥ m B ．若 m ⊂ α ， n ⊂ α ， l ⊥ m ， l ⊥ n ，则 l ⊥ α C ．若 l ∥ m ， m ∥ n ， l ⊥ α ，则 n ⊥ α D ．若 m ∥ α ， n ∥ β ， α ∥ β ，则 m ∥ n 解析： A 项中， l ∥ β 或 l ⊂ β ， m 与 l 可能异面或相交，故 A 错误； B 项中，若 m ∥ n ，则无法得出 l ⊥ α ，故 B 错误； C 项中，由 l ∥ m 及 m ∥ n ，可得 l ∥ n ，又 l ⊥ α ，所以 n ⊥ α ，故 C 正确； D 项中， m 与 n 可能相交或异面，故 D 错误．故选 C. 答案： C 平面与平面垂直的判定及性质 1 ．平面与平面垂直的判定定理 2 ．平面与平面垂直的性质定理 3. 垂直关系的转化 ____________________[ 通关方略 ]____________________ 1 ．两个平面互相垂直是两个平面相交的特殊情形． 2 ．由平面和平面垂直的判定定理可知，要证明平面与平面垂直，可转化为从现有直线中寻找平面的垂线，即证明线面垂直． 3 ．平面和平面垂直的判定定理的两个条件： l ⊂ α ， l ⊥ β ，缺一不可． 3 ． (2014 年郑州模拟 ) 设 a 、 b 是两条不同的直线， α 、 β 是两个不同的平面，则下列四个命题： ① 若 a ⊥ b ， a ⊥ α ， b ⊄ α ，则 b ∥ α ； ② 若 a ∥ α ， a ⊥ β ，则 α ⊥ β ； ③ 若 a ⊥ β ， α ⊥ β ，则 a ∥ α 或 a ⊂ α ； ④ 若 a ⊥ b ， a ⊥ α ， b ⊥ β ，则 α ⊥ β . 其中正确命题的个数为 ( 　　 ) A ． 1 　　　　 B ． 2 　　　　 C ． 3 　　　　 D ． 4 解析： 通过线面垂直及平行的判定定理和性质定理，可以判断四个命题都正确，故选 D. 答案： D 4. 如图，在正四面体 P － ABC 中， D 、 E 、 F 分别是 AB 、 BC 、 CA 的中点，下面四个结论不成立的是 ( 　　 ) A ． BC ∥ 平面 PDF B ． DF ⊥ 平面 PAE C ．平面 PDF ⊥ 平面 PAE D ．平面 BDE ⊥ 平面 ABC 解析： 因 BC ∥ DF ，所以 BC ∥ 平面 PDF ， A 成立；易证 BC ⊥ 平面 PAE ， BC ∥ DF ，所以结论 B 、 C 均成立；点 P 在底面 ABC 内的射影为 △ ABC 的中心，不在中位线 DE 上，故结论 D 不成立． 答案： D 垂直关系的基本问题 【 例 1】 　 (1) 设 a ， b 是夹角为 30° 的异面直线，则满足条件 “ a ⊂ α ， b ⊂ β ，且 α ⊥ β ” 的平面 α ， β ( 　　 ) A ．不存在　　　　　 B ．有且只有一对 C ．有且只有两对 D ．有无数对 (2) 已知直线 l ⊥ 平面 α ，直线 m ⊂ 平面 β ，有下列命题： ① α ∥ β ⇒ l ⊥ m ； ② α ⊥ β ⇒ l ∥ m ； ③ l ∥ m ⇒ α ⊥ β ； ④ l ⊥ m ⇒ α ∥ β . 其中，正确的命题序号有 ________ ． [ 解析 ] 　 (1) 过直线 a 的平面 α 有无数个．当平面 α 与直线 b 平行时，两直线的公垂线与 b 确定的平面 β ⊥ α ；当平面 α 与 b 相交时，过交点作平面 α 的垂线与 b 确定的平面 β ⊥ α ，故选 D. (2) ① 正确， ∵ l ⊥ α ， α ∥ β ， ∴ l ⊥ β ，又 m ⊂ β ， ∴ l ⊥ m ； ② 错误； l ， m 还可以垂直，斜交或异面； ③ 正确； ∵ l ⊥ α ， l ∥ m ， ∴ m ⊥ α ，又 m ⊂ β ， ∴ α ⊥ β ； ④ 错误； α 与 β 可能相交． [ 答案 ] 　 (1)D 　 (2) ①③ 反思总结 解决垂直关系的基本问题要注意 (1) 紧扣垂直关系的判定定理与性质定理． (2) 借助于图形去判断． (3) 举反例排除去判断． 变式训练 1 ． (2014 年惠州调研 ) 设 α ， β 为不重合的平面， m ， n 为不重合的直线，则下列命题正确的是 ( 　　 ) A ．若 α ⊥ β ， α ∩ β ＝ n ， m ⊥ n ，则 m ⊥ α B ．若 m ⊂ α ， n ⊂ β ， m ⊥ n ，则 n ⊥ α C ．若 n ⊥ α ， n ⊥ β ， m ⊥ β ，则 m ⊥ α D ．若 m ∥ α ， n ∥ β ， m ⊥ n ，则 α ⊥ β 解析： 与 α ， β 两垂直相交平面的交线垂直的直线 m ，可与 α 平行，故 A 错误；对 B ，存在 n ∥ α 的情况，故 B 错误；对 D ，存在 α ∥ β 的情况，故 D 错误；由 n ⊥ α ， n ⊥ β ，可知 α ∥ β ，又 m ⊥ β ，所以 m ⊥ α ，故 C 正确，选 C. 答案： C 直线与平面垂直的判定与性质 [ 解析 ] 　 (1) 证明： 因为 BC ＝ CD ，即 △ BCD 为等腰三角形， 又 ∠ ACB ＝ ∠ ACD ，故 BD ⊥ AC . 因为 PA ⊥ 底面 ABCD ，所以 PA ⊥ BD . 从而 BD 与平面 PAC 内两条相交直线 PA ， AC 都垂直，所以 BD ⊥ 平面 PAC . 解析： 由条件知， BD ⊥ 平面 PAC ，所以 PC ⊥ BD . 又 BC ＝ DC ，故过 D 作 DF ⊥ PC ，连接 BF ，则 BF ⊥ PC ， ∴ 存在点 F 使 PC ⊥ 面 BDF . 反思总结 证明直线和平面垂直的常用方法有 (1) 利用判定定理； (2) 利用判定定理的推论 ( a ∥ b ， a ⊥ α ⇒ b ⊥ α ) ； (3) 利用面面平行的性质 ( a ⊥ α ， α ∥ β ⇒ a ⊥ β ) ； (4) 利用面面垂直的性质． 当两个平面垂直时，在一个平面内垂直于交线的直线垂直于另一个平面． 解析： (1) 证明：因为 AB ＝ AC ， D 是 BC 的中点，所以 AD ⊥ BC . ① 又在直三棱柱 ABC － A 1 B 1 C 1 中， BB 1 ⊥ 平面 ABC ，而 AD ⊂ 平面 ABC ，所以 AD ⊥ BB 1 . ② 由 ① ， ② 得 AD ⊥ 平面 BB 1 C 1 C . 由点 E 在棱 BB 1 上运动，得 C 1 E ⊂ 平面 BB 1 C 1 C ，所以 AD ⊥ C 1 E . 平面与平面垂直的判定与性质 【 例 3】 　 (2014 年商丘质检 ) 如图，在平行四边形 ABCD 中， AB ＝ 2 BC ＝ 4 ， ∠ ABC ＝ 120° ， E ， M 分别为 AB ， DE 的中点，将 △ ADE 沿直线 DE 翻折成 △ A ′ DE ， F 为 A ′ C 的中点， A ′ C ＝ 4. (1) 求证：平面 A ′ DE ⊥ 平面 BCD ； (2) 求证： FB ∥ 平面 A ′ DE . [ 证明 ] 　 (1) 由题意， △ A ′ DE 是 △ ADE 沿 DE 翻折而成的， ∴△ A ′ DE ≌△ ADE . ∵∠ ABC ＝ 120° ，四边形 ABCD 是平行四边形， ∴∠ A ＝ 60°. 又 ∵ AD ＝ AE ＝ 2 ， ∴△ A ′ DE 和 △ ADE 都是等边三角形． 如图，连接 A ′ M ， MC ， ∵ M 是 DE 的中点， (2) 取 DC 的中点 N ，连接 FN ， NB . ∵ A ′ C ＝ DC ＝ 4 ， F ， N 分别是 A ′ C ， DC 的中点， ∴ FN ∥ A ′ D . 又 ∵ N ， E 分别是平行四边形 ABCD 的边 DC ， AB 的中点， ∴ BN ∥ DE . 又 ∵ A ′ D ∩ DE ＝ D ， FN ∩ NB ＝ N ， ∴ 平面 A ′ DE ∥ 平面 FNB . ∵ FB ⊂ 平面 FNB ， ∴ FB ∥ 平面 A ′ DE . 反思总结 1 ． 判定面面垂直的方法 (1) 面面垂直的定义； (2) 面面垂直的判定定理 ( a ⊥ β ， a ⊂ α ⇒ α ⊥ β ) ． 2 ．在已知平面垂直时，一般要用性质定理进行转化． 在一个平面内作交线的垂线，转化为线面垂直，然后进一步转化为线线垂直． 变式训练 3. 如图，在四棱锥 P － ABCD 中，平面 PAD ⊥ 平面 ABCD ， AB ＝ AD ， ∠ BAD ＝ 60° ， E ， F 分别是 AP ， AD 的中点． 求证： (1) 直线 EF ∥ 平面 PCD ； (2) 平面 BEF ⊥ 平面 PAD . 证明： (1) 在 △ PAD 中，因为 E ， F 分别为 AP ， AD 的中点，所以 EF ∥ PD . 又因为 EF ⊄ 平面 PCD ， PD ⊂ 平面 PCD ， 所以直线 EF ∥ 平面 PCD . (2) 连接 BD . 因为 AB ＝ AD ， ∠ BAD ＝ 60° ，所以 △ ABD 为正三角形．因为 F 是 AD 的中点，所以 BF ⊥ AD . 因为平面 PAD ⊥ 平面 ABCD ， BF ⊂ 平面 ABCD ， 平面 PAD ∩ 平面 ABCD ＝ AD ，所以 BF ⊥ 平面 PAD . 又因为 BF ⊂ 平面 BEF ，所以平面 BEF ⊥ 平面 PAD . —— 平行与垂直的综合问题 空间线面平行，垂直的综合问题一直是命题的热点，多以解答题形式考查，此类题目重点考查了线、面、平行，垂直的判定与性质，解答时易忽视平行垂直判定与性质定理中满足条件． 【 典例 】 　 (2013 年高考北京卷 )( 本题满分 14 分 ) 如图，在四棱锥 P － ABCD 中， AB ∥ CD ， AB ⊥ AD ， CD ＝ 2 AB ，平面 PAD ⊥ 底面 ABCD ， PA ⊥ AD ， E 和 F 分别是 CD 和 PC 的中点．求证： (1) PA ⊥ 底面 ABCD ； (2) BE ∥ 平面 PAD ； (3) 平面 BEF ⊥ 平面 PCD . [ 教你快速规范审题 ] 1 ．审条件，挖解题信息 2 ．审结论，明解题方向 3 ．建联系，找解题突破口 [ 教你准确规范解答 ] (1) 因为平面 PAD ⊥ 底面 ABCD ，且 PA 垂直于这两个平面的交线 AD ， 所以 PA ⊥ 底面 ABCD .3 分 (2) 因为 AB ∥ CD ， CD ＝ 2 AB ， E 为 CD 的中点， 所以 AB ∥ DE ，且 AB ＝ DE .4 分 所以 ABED 为平行四边形． 所以 BE ∥ AD .6 分 又因为 BE ⊄ 平面 PAD ， AD ⊂ 平面 PAD ， 所以 BE ∥ 平面 PAD .8 分 (3) 因为 AB ⊥ AD ，而且 ABED 为平行四边形． 所以 BE ⊥ CD ， AD ⊥ CD ， 10 分 由 (1) 知 PA ⊥ 底面 ABCD . 所以 PA ⊥ CD . 所以 CD ⊥ 平面 PAD . 所以 CD ⊥ PD .12 分 因为 E 和 F 分别是 CD 和 PC 的中点， 所以 PD ∥ EF . 又因为 CD ⊥ EF . EF ∩ BE ＝ E ， 所以 CD ⊥ 平面 BEF .13 分 所以平面 BEF ⊥ 平面 PCD .14 分 [ 常见失分探因 ] 易漏写 BE ⊄ 平面 PAD ， AD ⊂ 平面 PAD 而失分 _______________ [ 教你一个万能模板 ] _________________ 本小节结束 请按 ESC 键返回