2020-2021学年数学新教材人教B版必修第四册课时分层作业：11 7页

www.ks5u.com 课时分层作业(十六)　平行直线与异面直线 ‎(建议用时：40分钟)‎ 一、选择题 ‎1．在三棱锥SABC中，与SA是异面直线的是(　　)‎ A．SB B．SC C．BC D．AB C　[如图所示，SB，SC，AB，AC与SA均是相交直线，BC与SA既不相交，又不平行，是异面直线．‎ ‎]‎ ‎2．分别在两个平面内的两条直线的位置关系是(　　)‎ A．异面 B．平行 C．相交 D．以上都有可能 D　[如图，在长方体ABCDA1B‎1C1D1中，直线AD1在平面AA1D1D中，直线BB1，BC1分别在平面BB‎1C1C中，但AD1∥BC1，AD1与BB1异面，又直线AB在平面ABCD中，显然AD1∩AB＝A．]‎ ‎3．如图所示，在长方体ABCDA1B‎1C1D1中，A‎1C1与B1D1相交于点O，E，F分别是B1O，C1O的中点，则长方体的各棱中与EF平行的有(　　)‎ A．3条 B．4条 C．5条 D．6条 B　[由于E，F分别是B1O，C1O的中点，故EF∥B‎1C1，因为和棱B‎1C1平行的棱有AD，BC，A1D1，所以符合题意的棱共有4条．]‎ ‎4．下列命题中，错误的结论是(　　)‎ A．如果一个角的两边与另一个角的两边分别平行，那么这两个角相等 B．如果两条相交直线和另两条相交直线分别平行，那么这两组直线所成的锐角(或直角)相等 C．如果一个角的两边和另一个角的两边分别垂直，那么这两个角相等或互补 D．如果两条直线同时平行于第三条直线，那么这两条直线互相平行 A　[选项A中，如果一个角的两边与另一个角的两边分别平行，那么这两个角相等或互补，故选项A错误；选项B中，如果两条相交直线和另两条相交直线分别平行，那么这两组直线所成的锐角或直角相等，故选项B正确；选项C中，如果一个角的两边和另一个角的两边分别垂直，两角相等或互补，故选项C正确；选项D中，如果两条直线同时平行于第三条直线，那么这两条直线平行，故选项D正确．]‎ ‎5．如图，在正方体ABCDA1B‎1C1D1中，E，F，G，H，M，N分别是棱AB，BC，A1B1，BB1，C1D1，CC1的中点，则下列结 论正确的是(　　)‎ A．直线GH和MN平行，GH和EF相交 B．直线GH和MN平行，MN和EF相交 C．直线GH和MN相交，MN和EF异面 D．直线GH和EF异面，MN和EF异面 B　[易知GH∥MN，又∵E，F，M，N分别为所在棱的中点，由基本事实3可知EF，DC，MN交于一点，故选B．]‎ 二、填空题 ‎6．空间四边形ABCD中，M，N分别为AB，CD的中点，则MN________(AC＋‎ BD)(填“≥”“＞”“≤”“＜”“＝”符号)．‎ ‎＜　[取BC中点E，连接EM、EN(图略)，则 相加EM＋EN＝(AC＋BD)，‎ 又EM＋EN＞MN，所以MN＜(AC＋BD)．]‎ ‎7．a，b，c是空间中的三条直线，下面给出四个命题：‎ ‎①若a∥b，b∥c，则a∥c；‎ ‎②若a与b相交，b与c相交，则a与c相交；‎ ‎③若a⊂平面α，b⊂平面β，则a，b一定是异面直线；‎ 其中正确的命题是________．(只填序号)‎ ‎①　[由平行线的传递性知①正确；当a与b相交，b与c相交时，a与c可以相交、平行，也可以异面，故②不正确；a⊂α，b⊂β，并不能说明a与b“不同在任何一个平面内”，故③不正确．]‎ ‎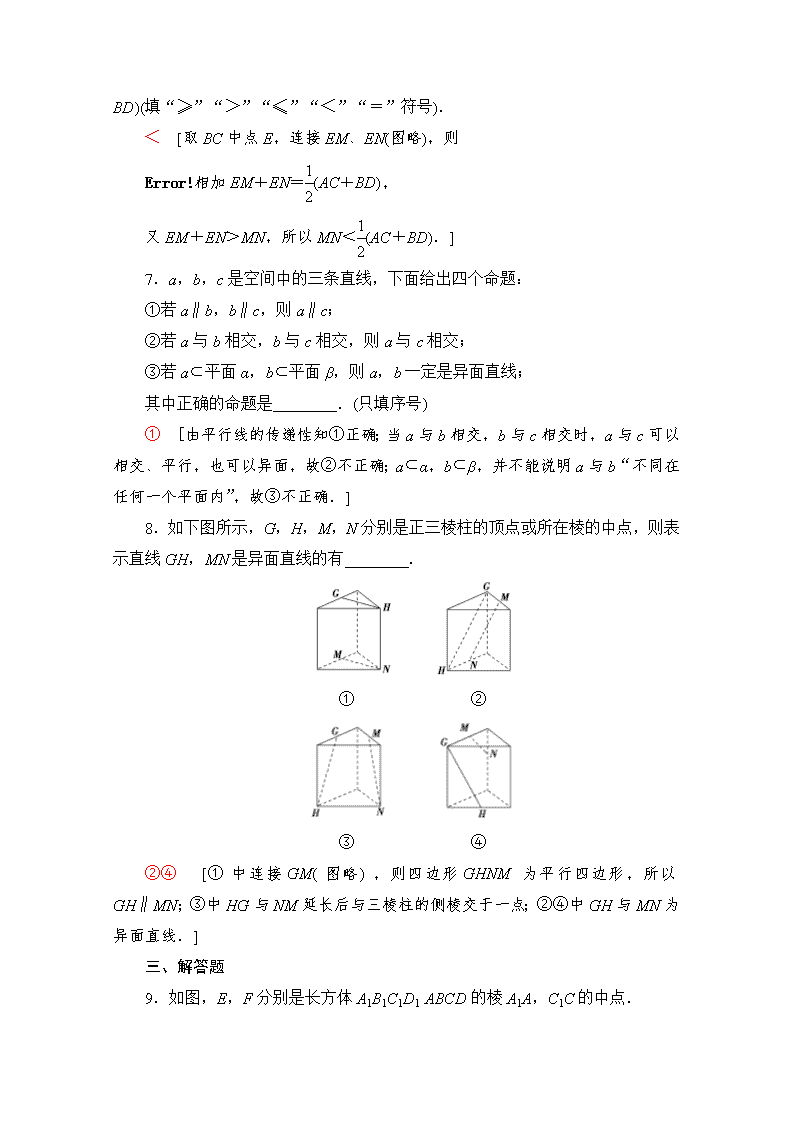8．如下图所示，G，H，M，N分别是正三棱柱的顶点或所在棱的中点，则表示直线GH，MN是异面直线的有________．‎ ‎①　　　　　　　 ②‎ ‎③　　　　 　　 ④‎ ‎②④　[①中连接GM(图略)，则四边形GHNM为平行四边形，所以GH∥MN；③中HG与NM延长后与三棱柱的侧棱交于一点；②④中GH与MN为异面直线．]‎ 三、解答题 ‎9．如图，E，F分别是长方体A1B‎1C1D1ABCD的棱A‎1A，C‎1C的中点．‎ 求证：四边形B1EDF是平行四边形．‎ ‎[证明]　设Q是DD1的中点，连接EQ，QC1，‎ ‎∵E是AA1的中点，‎ ‎∴EQA1D1，‎ 又在矩形A1B‎1C1D1中，A1D1B‎1C1，‎ ‎∴EQB‎1C1，‎ ‎∴四边形EQC1B1为平行四边形，‎ ‎∴B1EC1Q.‎ 又∵Q，F分别是矩形DD‎1C1C的边DD1，CC1的中点，‎ ‎∴QDC‎1F，‎ ‎∴四边形DQC‎1F为平行四边形，‎ ‎∴C1QDF，‎ 又∵B1EC1Q，∴B1EDF，‎ ‎∴四边形B1EDF为平行四边形．‎ ‎10．在平行六面体ABCDA1B‎1C1D1中，M，N，P分别是CC1，B‎1C1，C1D1的中点．求证：∠NMP＝∠BA1D．‎ ‎[解]　如图，连接CB1，CD1，‎ ‎∵CDA1B1，‎ ‎∴四边形A1B1CD是平行四边形，‎ ‎∴A1D∥B‎1C．‎ ‎∵M，N分别是CC1，B‎1C1的中点，‎ ‎∴MN∥B‎1C，∴MN∥A1D．‎ ‎∵BCA1D1，∴四边形A1BCD1是平行四边形，‎ ‎∴A1B∥CD1.‎ ‎∵M，P分别是CC1，C1D1的中点，∴MP∥CD1，‎ ‎∴MP∥A1B，‎ ‎∴∠NMP和∠BA1D的两边分别平行且方向都相反，‎ ‎∴∠NMP＝∠BA1D．‎ ‎11．若直线l1和l2是异面直线，l1在平面α内，l2在平面β内，l是平面α与平面β的交线，则下列命题正确的是(　　)‎ A．l与l1，l2都不相交 B．l与l1，l2都相交 C．l至多与l1，l2中的一条相交 D．l至少与l1，l2中的一条相交 D　[若直线l1，l2和l都不相交，则直线l1，l2都和l平行，则直线l1，l2平行，这和题中这两条直线异面相矛盾，所以l至少要与l1，l2中的一条相交．]‎ ‎12．(多选题)如图，在四面体ABCD中，M，N，P，Q，E分别是AB，BC，CD，AD，AC的中点，则下列说法中正确的是(　　)‎ A．M，N，P，Q四点共面 B．∠QME＝∠CBD C．△BCD∽△MEQ D．四边形MNPQ为梯形 ABC　[由中位线定理，易知MQ∥BD，ME∥BC，QE∥CD，NP∥BD．‎ 对于A，有MQ∥NP，所以M，N，P，Q四点共面，故A说法正确；对于B，根据等角定理，得∠QME＝∠CBD，故B说法正确；对于C，由等角定理，知∠QME＝∠CBD，∠MEQ＝∠BCD，所以△BCD∽△MEQ，故C说法正确；对于D，由三角形的中位线定理，知MQBD，NPBD，所以MQNP，所以四边形MNPQ为平行四边形，故D说法不正确．]‎ ‎13．如图，点P在平面ABC外，点F在BC的延长线上，E在线段PA上，则直线AB，BC，AC，EF，AP，BP中有________对异面直线．‎ ‎5　[异面直线有5对，分别是AB与EF，BC与AP，AC与BP，AC与EF，EF与BP.]‎ ‎14．(一题两空)如图，在三棱锥ABCD中，E，F，G，H分别是棱AB，BC，CD，DA的中点，则当AC，BD满足条件________时，四边形EFGH为菱形，当AC，BD满足条件________时，四边形EFGH是正方形．‎ AC＝BD　AC＝BD且AC⊥BD　[易知EH∥BD∥FG，且EH＝BD＝FG，同理EF∥AC∥HG，且EF＝AC＝HG，显然四边形EFGH为平行四边形．要使平行四边形EFGH为菱形需满足EF＝EH，即AC＝BD；要使四边形EFGH为正方形需满足EF＝EH且EF⊥EH，即AC＝BD且AC⊥BD．]‎ ‎15．如图，在正方体ABCDA1B‎1C1D1中，M，N分别是A1B1，B‎1C1的中点．‎ ‎(1)AM和CN是不是异面直线？并说明理由．‎ ‎(2)D1B和CC1是不是异面直线？并说明理由．‎ ‎[解]　连接A‎1C1，MN，B1D1(图略)．‎ ‎(1)AM和CN不是异面直线．理由如下：‎ ‎∵M，N分别是A1B1，B‎1C1的中点，∴MN∥A‎1C1.‎ 又∵A‎1AC‎1C，∴四边形A1ACC1为平行四边形．‎ ‎∴A‎1C1∥AC，∴MN∥AC，∴A，M，N，C在同一个平面内，‎ 故AM和CN不是异面直线．‎ ‎(2)D1B和CC1是异面直线．理由：‎ 选平面BCC1B1作参照，因为CC1⊂平面BCC1B1，‎ B∈平面BCC1B1，但D1∉平面BCC1B1，且B∉直线CC1，‎ 因此D1B和CC1是异面直线．‎