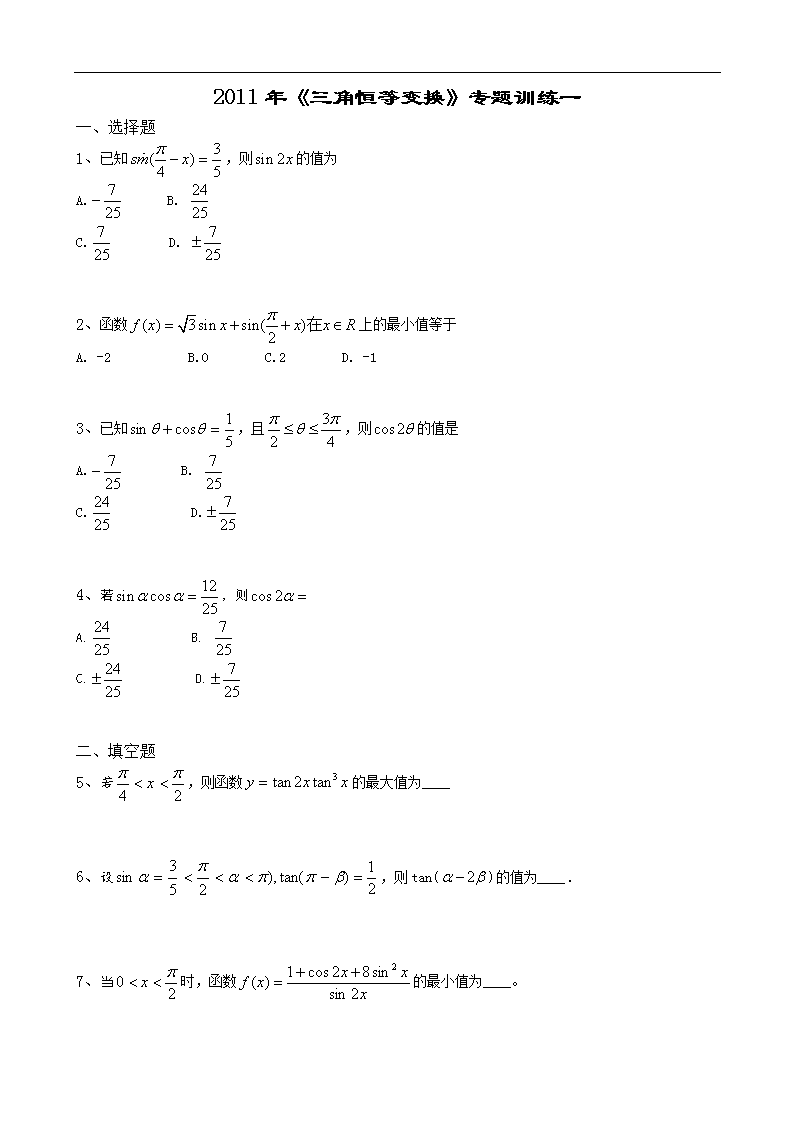2011高考数学专题复习：《三角恒等变换》专题训练一 6页

‎2011年《三角恒等变换》专题训练一 一、选择题 ‎1、已知，则的值为 A. B. ‎ C. D. ‎ ‎2、函数上的最小值等于 A. -2 B.O C.2 D. -1‎ ‎3、已知，且，则的值是 A. B. ‎ C. D.‎ ‎4、若，则 A. B. ‎ C. D.‎ 二、填空题 ‎5、若，则函数的最大值为____‎ ‎6、设，则tan()的值为____．‎ ‎7、当时，函数的最小值为____。‎ ‎8、若，则=____．‎ ‎9、如果．且，那么____．‎ ‎10、已知函数，又，若的最小值为，则正数的值为____．‎ 三、解答题 ‎11、如图13 -1，，是单位圆O上的点，，分别是圆0与轴的两个交点，△为正三角形．‎ ‎(1)若点的坐标为求的值；‎ ‎(2)若，四边形的周长为，试将表示成的函数，并求出的最大值．‎ ‎12、在△ABC中，，，分别是角，，的对边，，且//．‎ ‎(1)求角的大小；‎ ‎(2)求的值域．‎ ‎13、已知锐角△ABC中，三个内角为，，，两向量 ‎，若与是共线向量．‎ ‎(1)求角的大小；‎ ‎(2)求函数取最大值时角的大小．‎ ‎14、已知向量 ‎(1)求的值；‎ ‎(2)若，且，求的值．‎ ‎15、已知．且 ‎(1)求的值；‎ ‎(2)求.‎ 以下是答案 一、选择题 ‎1、 解析 ‎ ‎2、A 解析 由于，‎ 故其最小值为-2。‎ ‎3、解析。由于 即。又 ‎，于是 ‎4、 解析:‎ 二、填空题 ‎5、-8 解析 ‎ ‎6、 解析 ‎ 由。得 ‎，故于是 ‎7、4解析 当且仅当，即时，取=。‎ 存在x.使，这时．‎ ‎8、 解析 ‎ 所以，因此 ‎9、 解析 ‎ ‎10、 解析 又由．且的最小值为.可知,于是 三、解答题 ‎11、(1)设，由已知得，‎ ‎12、(1)由得由正弦定理，得 由(1)得 ‎13、‎ 化简得，‎ ‎△ABC为锐角三角形，‎ ‎，当B =60。时函数取得最大值2．‎ ‎14、‎ 解得 由，得由，得 ‎15、(1)由 ‎(2)由叉 由得，‎