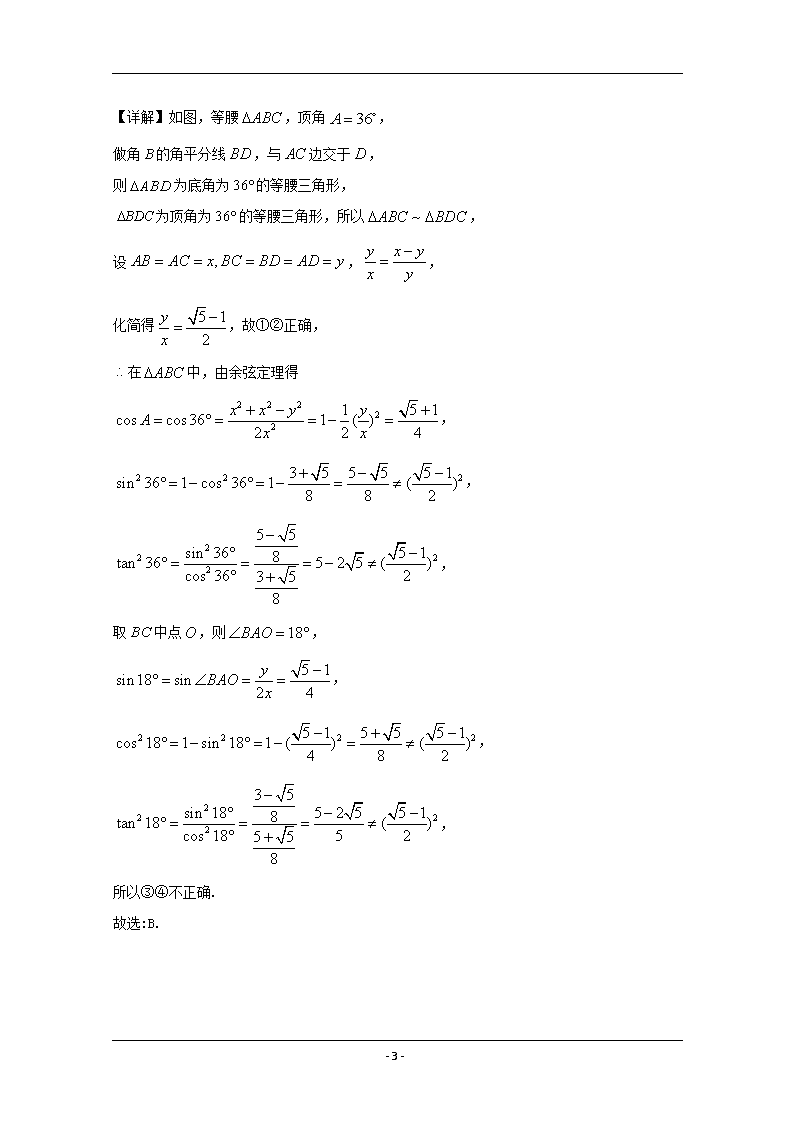开卷教育联盟全国2020届高三模拟考试（二）数学（理）试题 Word版含解析 23页

www.ks5u.com 开卷教育联盟 2020届全国高三模拟考试(二)‎ 数学(理科)‎ 一､选择题(本题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的)‎ ‎1.已知集合，，则（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 先求得集合,再根据并集的定义求解即可.‎ ‎【详解】 ，选B ‎【点睛】本题考查了一元二次不等式的解法，集合的并集运算，是基础题.‎ ‎2.（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 利用复数的四则运算，直接对所求式子运算即可得答案.‎ ‎【详解】.‎ 故选：D.‎ ‎【点睛】本题考查复数的四则运算，考查基本运算求解能力，属于基础题.‎ ‎3.设函数，的定义域都为，且是奇函数，是偶函数，则下列结论正确的是（ ）‎ A. 是偶函数 B. 是奇函数 C. 是奇函数 D. 是奇函数 - 23 -‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 根据函数奇偶性的性质即可得到结论．‎ ‎【详解】解：是奇函数，是偶函数，‎ ‎，，‎ ‎，故函数是奇函数，故错误，‎ 为偶函数，故错误，‎ 是奇函数，故正确．‎ 为偶函数，故错误，‎ 故选：．‎ ‎【点睛】本题主要考查函数奇偶性的判断，根据函数奇偶性的定义是解决本题的关键．‎ ‎4.古希腊时期，人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是，称为黄金分割比，我们把有两条边长之比为的三角形称为黄金三角形.则下列结论，正确的个数是（ ）‎ ‎①顶角等于的等腰三角形是黄金三角形；‎ ‎②底角等于的等腰三角形是黄金三角形；‎ ‎③有一个角等于的直角三角形是黄金三角形；‎ ‎④有一个角等于的直角三角形是黄金三角形.‎ A. 1 B. 2 C. 3 D. 4‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 如图等腰，顶角，做底角的角平分线，可得为底角为的等腰三角形，设，推出，即可求出关系，可判断①②的真假，再通过解三角形求得，的三角函数，可判断③④真假.‎ - 23 -‎ ‎【详解】如图，等腰，顶角，‎ 做角的角平分线，与边交于，‎ 则为底角为的等腰三角形，‎ 为顶角为的等腰三角形，所以，‎ 设，，‎ 化简得，故①②正确，‎ 在中，由余弦定理得 ‎，‎ ‎，‎ ‎，‎ 取中点，则，‎ ‎，‎ ‎，‎ ‎，‎ 所以③④不正确.‎ 故选:B.‎ - 23 -‎ ‎【点睛】‎ 本题以数学文化为背景，考查等腰三角形的性质、求三角函数值，考查计算求解能力，属于中档题.‎ ‎5.已知函数，则y＝f（x）的图象大致为（ ）‎ A. B. ‎ C. D. ‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 利用特殊值判断函数的图象即可．‎ ‎【详解】令，则，再取，则，显然，故排除选项B、C；‎ 再取时，，又当时，，故排除选项D.‎ 故选：A.‎ - 23 -‎ ‎【点睛】本题考查函数的图象的判断，特殊值法比利用函数的导函数判断单调性与极值方法简洁，属于基础题.‎ ‎6.唐宋八大家，又称唐宋古文八大家，是中国唐代韩愈､柳宗元，宋代苏洵､苏轼､苏辙､王安石､曾巩､欧阳修八位散文家的合称.他们先后掀起的古文革新浪潮，使诗文发展的陈旧面貌焕然一新.在唐宋八大家中随机取两位，则他们来自同一朝代的概率是（ ）‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 先求出八大家随机取两位的方法数为，再求出两个来自同一朝代的有，即可求解.‎ ‎【详解】在唐宋八大家中随机取两位，‎ 则他们来自同一朝代的概率是.‎ 故选:A.‎ ‎【点睛】本题考查古典概型的概率，利用组合数公式是解题的关键，属于基础题.‎ ‎7.中，边的高为，若，，，，，则（ )‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】‎ ‎【详解】试题分析：由，，可知 ‎8. 执行右面的程序框图，如果输入的t∈[－1，3]，则输出的s属于( )‎ - 23 -‎ A. [－3,4] B. [－5,2]‎ C. [－4,3] D. [－2,5]‎ ‎【答案】A ‎【解析】‎ 试题分析：此程序为分段函数，当时，，当时，，所以函数的值域为：，故选A．‎ 考点：程序框图 ‎9.已知数列的通项公式为，则数列（ ）‎ A. 有最大项，没有最小项 B. 有最小项，没有最大项 C. 既有最大项又有最小项 D. 既没有最大项也没有最小项 ‎【答案】C ‎【解析】‎ ‎【分析】‎ 将化为，其中；结合二次函数的性质和的取值可确定最值的取得情况，从而得到结果.‎ - 23 -‎ ‎【详解】由题意得：‎ 令，则 ‎ 对称轴为，在上单调递减，在上单调递增 当时，取最小值；当时，取最大值 既有最大项又有最小项 故选：‎ ‎【点睛】本题考查数列最大项和最小项的求解问题，关键是能够将通项公式化为二次函数的形式，根据二次函数性质求得结果；易错点是忽略数列中的取值的限制及换元后参数的取值限制，造成求解错误.‎ ‎10.如图，在正四棱柱中，底面的边长为3，与底面所成角的大小为，且，则该正四棱柱的外接球表面积为（ ）‎ A. B. ‎ C. D. ‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 长方体外接球的直径为长方体的对角线，与底面所成的角为，从而有，求出即可.‎ ‎【详解】连正四棱柱，‎ 平面为与底面所成角，‎ - 23 -‎ ‎，‎ 在中，，‎ ‎，‎ 正四棱柱的外接球半径为，‎ 其表面积为.‎ 故选:A.‎ ‎【点睛】本题考查多面体与球的“接”“切”问题，注意直线与平面所成角的几何求法，属于基础题.‎ ‎11.（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 化切为弦，分式通分，引进特殊角，非特殊角相消相约，即可求解.‎ ‎【详解】原式 ‎.‎ 故选:C.‎ ‎【点睛】本题考查非特殊角求值、三角恒等变换应用，考查计算求解能力，属于中档题.‎ ‎12.如图，为椭圆的长轴的左、右端点，为坐标原点，‎ - 23 -‎ 为椭圆上不同于的三点，直线，围成一个平行四边形，则（ ）‎ A 5 B. C. 9 D. 14‎ ‎【答案】D ‎【解析】‎ 试题分析：设，斜率为，则斜率为，且 ‎，所以，同理，因此，选D.‎ 考点：解析几何定值问题 ‎【思路点睛】定点、定值问题通常是通过设参数或取特殊值来确定“定点”是什么、“定值”是多少，或者将该问题涉及的几何式转化为代数式或三角问题，证明该式是恒定的. 定点、定值问题同证明问题类似，在求定点、定值之前已知该值的结果，因此求解时应设参数，运用推理，到最后必定参数统消，定点、定值显现.‎ 二､填空题(本题共4小题，每小题5分，共20分.)‎ ‎13.已知，曲线在点处的切线的斜率为，则当取最小值时，的值为______.‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ - 23 -‎ 求导求出，得，利用基本不等式即可求解.‎ ‎【详解】由题意可得，因为，‎ 所以，‎ 当且仅当时，等号成立，取最小值为4.‎ 故答案为:.‎ ‎【点睛】本题考查导数的几何意义、基本不等式求最值，属于基础题.‎ ‎14.函数的图象可由函数的图象至少向右平移_______个长度单位得到．‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 利用两角和与差的正弦函数化简两个函数的表达式为同名函数，然后利用左加右减的原则确定平移的方向与单位.‎ ‎【详解】分别把两个函数解析式化简为：‎ ‎，‎ ‎，‎ 可知只需把函数的图象向右平移个单位长度，‎ 得到函数的图象，‎ 故答案是：.‎ ‎【点睛】该题考查的是有关函数图象的平移变换的问题，在解题的过程中，注意正确化简函数解析式，把握住平移的原则是左加右减，以及自变量本身的变化量.‎ ‎15.甲小组有2个男生和4个女生，乙小组有5个男生和3个女生，现随机地从甲小组抽出一名学生放入乙小组，然后从乙小组随机抽出一名学生，则从乙小组抽出女生的概率是______.‎ ‎【答案】‎ ‎【解析】‎ - 23 -‎ ‎【分析】‎ 对于从甲组抽出一名学生分男、女讨论，再结合独立事件同时发生的概率关系，和互斥事件概率，即可求解.‎ ‎【详解】根据题意，分两种情况讨论：‎ ‎①从甲小组中取出男生，其概率为，‎ 此时乙小组中有6个男生和3个女生，‎ 从乙小组中取出女生的概率为，‎ 则这种情况下的概率为.‎ ‎②从甲小组中取出女生，其概率为，‎ 此时乙小组中有5个男生和4个女生，‎ 从乙小组中取出女生的概率为，‎ 则这种情况下的概率为.‎ 则从乙小组中取出女生的概率是.‎ 故答案为:.‎ ‎【点睛】本题考查互斥事件、独立事件同时发生的概率，合理分类是解题的关键，属于基础题.‎ ‎16.已知双曲线：的渐近线与抛物线相切，则的离心率为______.‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 将渐近线方程与抛物线方程联立，利用相切只有一个实数解，求出，再由关系，即可求解.‎ ‎【详解】把代入得，‎ - 23 -‎ ‎∴，所以.‎ 故答案为:.‎ ‎【点睛】本题考查双曲线的性质，属于基础题.‎ 三､解答题(共70分，解答应写出文字说明､证明过程或演算步骤.第17~21题为必考题，每个试题考生都必须作答.第22､23题为选考题，考生根据要求作答.)‎ ‎17.为数列的前项和，已知，．‎ ‎（1）求的通项公式；‎ ‎（2）设，求数列的前项和．‎ ‎【答案】（1）；（2）‎ ‎【解析】‎ 试题分析：（1）由题意当时，，当时，，因为 ‎∴，即可求得通项公式；（2）因为，利用裂项求和法即可求得数列的前项和．‎ 试题解析：（1）依题意有①‎ 当时，，得；‎ 当时，②‎ 有①②得，‎ 因为，∴，‎ ‎∴成等差数列，得．‎ ‎（2），‎ - 23 -‎ 考点：等差数列的通项公式，裂项求和法 ‎18.如图，四棱锥中，底面为矩形，平面，为的中点.‎ ‎ ‎ ‎（1）证明:∥平面.‎ ‎（2）设二面角为，，，求三棱锥的体积.‎ ‎【答案】（1）见解析（2）‎ ‎【解析】‎ ‎【分析】‎ ‎(1)连结交于点，连结. 根据四边形为矩形，所以为的中点，为的中点，利用三角形的中位线可得∥，再利用线面平行的判定定理证明. ‎ ‎(2) 根据平面，四边形为矩形，建立空间直角坐标系.设，再求得平面DAE， 平面CAE的法向量，根据二面角为，利用，解得.，然后利用锥体体积公式求解.‎ ‎【详解】(1)连结交于点，连结. ‎ 因为四边形为矩形，所以为的中点，‎ 又为的中点，所以∥，‎ 且平面，平面，所以∥平面. ‎ ‎(2) 因为平面，四边形为矩形，所以两两垂直，‎ - 23 -‎ 以为坐标原点，的方向为轴的正方向，的方向为轴的正方向，的方向为轴的正方向，为单位长，建立空间直角坐标系.‎ 设，则， ‎ 所以， ‎ 设为平面的法向量，则，‎ 可取 ， ‎ 又为平面的一个法向量，由题设知 即，解得.‎ 因为为的中点，设为的中点，‎ 则∥，且，⊥面，‎ 故有三棱锥的高为， ‎ 三棱锥的体积 所以三棱锥的体积为.‎ - 23 -‎ ‎【点睛】本题主要考查线面平行的判定定理，二面角和三棱锥的体积，还考查了转化化归的思想和运算求解的能力，属于中档题.‎ ‎19.某校为了了解在校学生的支出情况，组织学生调查了该校2012年至2018年学生的人均月支出(单位：百元)的数据如下表：‎ 年份 ‎2012‎ ‎2013‎ ‎2014‎ ‎2015‎ ‎2016‎ ‎2017‎ ‎2018‎ 年份代号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ 人均月支出 ‎2.9‎ ‎3.3‎ ‎3.6‎ ‎4.4‎ ‎4.8‎ ‎5.2‎ ‎5.9‎ ‎（1）求关于的线性回归方程；‎ ‎（2）利用（1）中的回归方程，分析2012年至2018年该校学生人均月支出的变化情况，并预测该校2020年的人均月支出.‎ 附：回归直线的斜率和截距的最小二乘估计公式分别为：，.‎ ‎【答案】（1）.（2）2012年至2018年该校学生人均月支出逐年增加，平均每年增加0.5百元. 预测值为6.8百元 ‎【解析】‎ ‎【分析】‎ ‎（1）由已知数据分别求出公式中的量，即可求出求解；‎ ‎（2）根据系数的正负，分析月支出增加还是减少，将代入回归方程，即可求出结论.‎ ‎【详解】（1）由所给数据计算得 ‎，‎ ‎，‎ ‎，‎ - 23 -‎ ‎，‎ ‎，‎ ‎.‎ 所求回归方程为.‎ ‎（2）由（1）知，，‎ 故2012年至2018年该校学生人均月支出逐年增加，‎ 平均每年增加0.5百元.‎ 将2020年的年份代号代入（1）中的回归方程，‎ 得，‎ 故预测该校2020年人均月支出为6.8百元.‎ ‎【点睛】本题考查线性回归直线方程以及应用，考查计算求解能力，属于基础题.‎ ‎20.已知椭圆：的上､下顶点分别为，，且短轴长为，为椭圆上任意一点，直线，的斜率之积为，，依次为左､右焦点.‎ ‎（1）求椭圆的方程；‎ - 23 -‎ ‎（2）山不会忘记你，河不会忘记你，祖国不会忘记你!南仁东，“天眼”之父，被追授“时代楷模”荣誉称号.24年，8000多个日夜，500米口径球面射电望远镜首席科学家､总工程师南仁东心无旁骛，为崇山峻岭间的“中国天眼”燃尽生命，在世界天文史上镌刻下新的高度.“天眼”是世界上最大､最灵敏的单口径射电望远镜，它看似一口“大锅”，可以接收到百亿光年外的电磁信号.调试期的“天眼”已经发现了多颗脉冲星，成为国际瞩目的宇宙观测“利器”.在党的十九大报告中，“天眼”与天宫､蛟龙､大飞机等一起，被列为创新型国家建设的丰硕成果……南仁东来不及目睹.但他执着追求科学梦想的精神，将激励一代又一代科技工作者继续奋斗，勇攀世界科技高峰.在“天眼”的建设中大量用到了圆锥曲线的光学性质，请以上面的椭圆为代表，证明：由焦点发出的光线射到椭圆上任意一点后反射，反射光线必经过另一焦点.(温馨提示：光线射到曲线上某点反射时，法线垂直于该点处的切线)‎ ‎【答案】（1）.（2）答案见解析 ‎【解析】‎ ‎【分析】‎ ‎（1）由已知得坐标，设，结合斜率公式，即可求出椭圆方程；‎ ‎（2）设点坐标，根据已知求出切线斜率，进而求出法线方程，利用几何法证明法线是的角平分线即可.‎ ‎【详解】（1）设，直线，的斜率为，，‎ 由题意知，，‎ 由，得，‎ 整理得.即椭圆的方程为.‎ ‎（2）当为椭圆顶点时结论显然成立，‎ 当不是椭圆顶点时，要证结论只须证法线平分，‎ 设点坐标，‎ 设切于点的切线方程为，‎ 与椭圆方程联立，消去得，‎ ‎，‎ ‎，‎ ‎，‎ - 23 -‎ ‎，‎ 所以切线斜率为，所以法线斜率为，‎ 法线方程，‎ 令可得法线与轴交点的横坐标为，‎ ‎∴，‎ ‎，‎ ‎∴，‎ ‎，‎ ‎，‎ 或（舍去）‎ 所以法线平分，结论成立.‎ ‎【点睛】本题考查椭圆轨迹方程、直线与椭圆的位置关系，注意几何法证明椭圆的性质，意在考查直观想象、逻辑推理、数学计算能力，属于较难题.‎ - 23 -‎ ‎21.已知定义在的函数满足，且，(，是常数). ‎ ‎（1）当时，求在处的切线方程；‎ ‎（2）存在，使，求取值范围.‎ ‎【答案】（1）.（2）‎ ‎【解析】‎ ‎【分析】‎ ‎（1）当时，求出，得到切线的点斜式方程即可；‎ ‎（2）即求时，，由已知可得，令，可证恒成立，因此，进而得到单调性，求出的最小值，而，对分类讨论，得到其单调性，进而求出最大值，即可求出结论.‎ ‎【详解】（1）当时，，.‎ 故，又，‎ 所以切线方程为，即.‎ ‎（2）证明：由题意，在时，，‎ 因为满足，‎ 所以，令，‎ 则，‎ - 23 -‎ 当时，，单调递增，‎ 故时，有最大值，，‎ 所以，在内单调递减，，‎ 而.‎ 当时，在内，，单调递增，‎ ‎，∴；‎ 当时，在内，，单调递减，，∴，‎ 综上所述，的取值范围是 ‎【点睛】本题考查导数的综合应用，涉及到导数的几何意义、单调性、最值，不等式存在成立与最值之间的转化，意在考查逻辑推理、数学计算能力，属于较难题.‎ ‎22.‎ 在平面直角坐标系中，倾斜角为的直线的参数方程为（为参数）.以坐标原点为极点，轴正半轴为极轴建立极坐标系，曲线的极坐标方程为．‎ ‎（Ⅰ）求直线的普通方程和曲线的直角坐标方程；‎ ‎（Ⅱ）已知点，若点的极坐标为，直线经过点且与曲线相交于两点，设线段的中点为，求的值.‎ ‎【答案】（1）,（Ⅱ） ‎ ‎【解析】‎ - 23 -‎ 分析：（Ⅰ）将直线的参数方程中的参数消掉，得到直线的普通方程，将曲线的极坐标方程等号两边同乘以，再根据平面直角坐标与极坐标之间的转换关系，求得结果；‎ ‎（Ⅱ）根据题意，得到相应点的坐标，代入，求得对应直线的斜率，两个方程联立，求得弦的中点，之后应用两点间距离公式求得结果.‎ 详解：（Ⅰ）消去直线的参数方程中的参数，得到直线的普通方程为：，把曲线的极坐标方程 左右两边同时乘以，得到：，‎ 利用公式代入，化简出曲线的直角坐标方程：；‎ ‎（Ⅱ）点的直角坐标为，将点的直角坐标为代入直线中，得，即，联立方程组：，得中点坐标为，‎ 从而.‎ 点睛：该题考查的是有关坐标系与参数方程的问题，涉及到的知识点有参数方程向普通方程的转化，极坐标方程与平面直角坐标方程的转化，直线与曲线的交点，两点间距离问题，注意对公式的正确使用即可正确求得结果.‎ ‎23.已知函数，.‎ ‎（1）求的最小值；‎ ‎（2）记的最小值为，已知点在圆内(含边界)，求证：.‎ ‎【答案】（1）.（2）答案见解析 ‎【解析】‎ ‎【分析】‎ ‎（1）由绝对值不等式性质，即可求解；‎ ‎（2）根据柯西不等式拼凑，求出 - 23 -‎ 最大值，即可证明结论.‎ ‎【详解】（1）∵，‎ ‎∴.‎ ‎（2）证明：由（1）知，由柯西不等式得 ‎，‎ ‎∴，‎ 又点在圆内(含边界)，故，‎ ‎∴(当且仅当时取等号).‎ 即.‎ ‎【点睛】本题考查绝对值不等式的性质和柯西不等式的应用，考查计算求解能力，属于中档题.‎ - 23 -‎ - 23 -‎