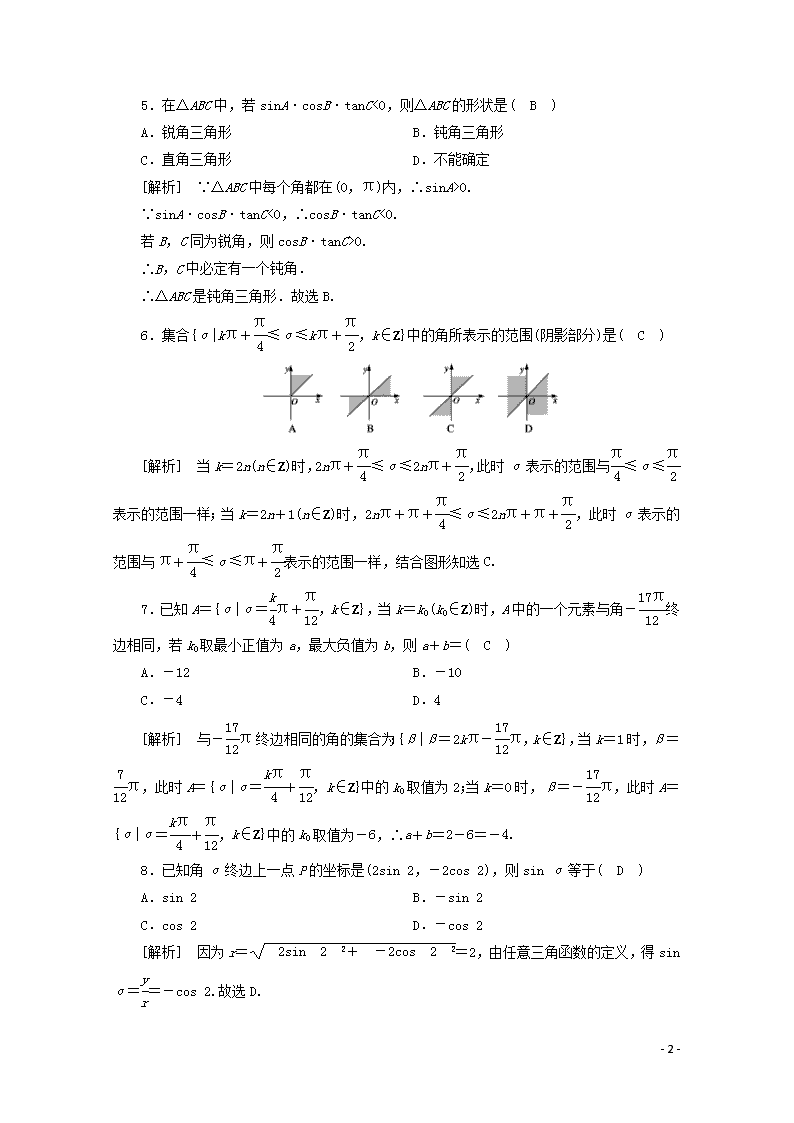高考数学一轮复习练案19第三章三角函数解三角形第一讲任意角和蝗制及任意角的三角函数含解析 6页

‎ [练案19]第三章　三角函数、解三角形 第一讲　任意角和弧度制及任意角的三角函数 A组基础巩固 一、单选题 ‎1．单位圆中，200°的圆心角所对的弧长为(　D　)‎ A．10π　 B．9π　‎ C．　 D． ‎[解析]　单位圆的半径r＝1,200°的弧度数是200×＝，由弧度数的定义知＝，所以l＝.故选D.‎ ‎2．(2020·河北唐山一中模拟)已知角α的终边过点P(－‎8m，－6sin 30°)，且cos α＝－，则m的值为(　B　)‎ A．－　 B．　‎ C．－　 D． ‎[解析]　由题意得，点P到原点的距离r＝，∴cos α＝＝－，∴m>0，∴＝，即m＝.‎ ‎3．(2020·河南省驻马店市期末)已知点P(tan α，cos α)在第三象限，则角α的终边在(　B　)‎ A．第一象限　　 B．第二象限 C．第三象限　　 D．第四象限 ‎[解析]　因为点P(tan α，cos α)在第三象限，‎ 所以，所以α为第二象限角，故选B.‎ ‎4．(2020·福建莆田二十四中月考)一个扇形的弧长与面积的数值都是6，则这个扇形的圆心角的弧度数是(　C　)‎ A．1　 B．2　‎ C．3　 D．4‎ ‎[解析]　设扇形的圆心角的弧度数为θ，半径为R.由题意得解得θ＝3，即扇形的圆心角的弧度数是3.故选C.‎ ‎5．在△ABC中，若sinA·cosB·tanC<0，则△ABC的形状是(　B　)‎ A．锐角三角形　　 B．钝角三角形 - 6 -‎ C．直角三角形　　 D．不能确定 ‎[解析]　∵△ABC中每个角都在(0，π)内，∴sinA>0.‎ ‎∵sinA·cosB·tanC<0，∴cosB·tanC<0.‎ 若B，C同为锐角，则cosB·tanC>0.‎ ‎∴B，C中必定有一个钝角．‎ ‎∴△ABC是钝角三角形．故选B. ‎ ‎6．集合{α|kπ＋≤α≤kπ＋，k∈Z}中的角所表示的范围(阴影部分)是(　C　)‎ ‎[解析]　当k＝2n(n∈Z)时，2nπ＋≤α≤2nπ＋，此时α表示的范围与≤α≤表示的范围一样；当k＝2n＋1(n∈Z)时，2nπ＋π＋≤α≤2nπ＋π＋，此时α表示的范围与π＋≤α≤π＋表示的范围一样，结合图形知选C.‎ ‎7．已知A＝{α|α＝π＋，k∈Z}，当k＝k0(k0∈Z)时，A中的一个元素与角－终边相同，若k0取最小正值为a，最大负值为b，则a＋b＝(　C　)‎ A．－12　 B．－10　‎ C．－4　 D．4‎ ‎[解析]　与－π终边相同的角的集合为：{β|β＝2kπ－π，k∈Z}，当k＝1时，β＝π，此时A＝{α|α＝＋，k∈Z}中的k0取值为2；当k＝0时，β＝－π，此时A＝{α|α＝＋，k∈Z}中的k0取值为－6，∴a＋b＝2－6＝－4.‎ ‎8．已知角α终边上一点P的坐标是(2sin 2，－2cos 2)，则sin α等于(　D　)‎ A．sin 2　 B．－sin 2　‎ C．cos 2　 D．－cos 2‎ ‎[解析]　因为r＝＝2，由任意三角函数的定义，得sin α＝＝－cos 2.故选D.‎ 二、多选题 ‎9．某人从家步行到学校，一般需要10分钟，则10分钟时间钟表的分针走过的角度是(　BD　)‎ - 6 -‎ A．　 B．－　‎ C．60°　 D．－60°‎ ‎[解析]　因为分针是按顺时针方向旋转的，故分针走过的角是负角，又分针旋转了10分钟，故分针走过的角是－60°.故选B、D.‎ ‎10．(2020·吉林长春普通高中模拟改编)若角α的顶点为坐标原点，始边在x轴的非负半轴上，终边在直线y＝－x上，则角α的取值集合是(　AD　)‎ A．{α|α＝2kπ－，或α＝2kπ＋，k∈Z}‎ B．{α|α＝2kπ＋，k∈Z}‎ C．{α|α＝kπ－，k∈Z}‎ D．{α|α＝kπ－，k∈Z}‎ ‎[解析]　因为直线y＝－x的倾斜角是，所以终边落在直线y＝－x上的角的取值集合为{α|α＝2kπ－或α＝2kπ＋，k∈Z}或{α|α＝kπ－，k∈Z}．故选A、D.‎ 三、填空题 ‎11．－2 020°角是第__二__象限角，与－2 020°角终边相同的最小正角是__140°__，最大负角是__－220°__.‎ ‎[解析]　∵－2 020°＝－6×360°＋140°，∴－2 020°角的终边与140°角的终边相同．‎ ‎∴－2 020°角是第二象限角，与－2 020°角终边相同的最小正角是140°.又是140°－360°＝－220°，故与－2 020°终边相同的最大负角是－220°.‎ ‎12．在直角坐标系xOy中，O是原点，A(，1)，将点A绕O逆时针旋转90°到B点，则B点坐标为　(－1，)　.‎ ‎[解析]　依题意知OA＝OB＝2，∠AOx＝30°，∠BOx＝120°，设点B坐标为(x，y)，所以x＝2cos 120°＝－1，y＝2sin 120°＝，即B(－1，)．‎ ‎13．一扇形是从一个圆中剪下的一部分，半径等于圆半径的，面积等于圆面积的.则扇形的弧长与圆的周长之比为　　.‎ ‎[解析]　设圆的半径为r，则扇形的半径为，记扇形的圆心角为α，则＝ - 6 -‎ ‎，所以α＝.所以扇形的弧长与圆的周长之比为＝＝.‎ ‎14．(2020·郑州模拟)函数y＝lg(2sinx－1)＋的定义域为　[2kπ＋，2kπ＋)(k∈Z)　.‎ ‎[解析]　要使原函数有意义，必须有：‎ 即 如图，在单位圆中作出相应三角函数线，‎ 由图可知，原函数的定义域为[2kπ＋，2kπ＋)(k∈Z)．‎ B组能力提升 ‎1．(2020·河北石家庄模拟)已知角α(0°≤α<360°)终边上一点的坐标为(sin150°，cos150°)，则α＝(　C　)‎ A．150°　 B．135°　‎ C．300°　 D．60°‎ ‎[解析]　sin150°＝>0，cos150°＝－<0，角α终边上一点的坐标为(，－)，故该点在第四象限，由三角函数的定义得sinα＝－，又0°≤α<360°，所以角α为300°，故选C.‎ ‎2．(2020·唐山模拟)函数f(x)＝＋＋的值域为(　D　)‎ A．{3,2,1}　　 B．{－1,2,1}‎ C．{－1,0,1}　　 D．{－1,3}‎ ‎[解析]　由sinx≠0，cosx≠0，知x终边不在坐标轴上，若x为第一象限角，f(x)＝＋＋＝3.‎ 若x为第二象限角，f(x)＝＋＋＝－1.‎ - 6 -‎ 若x为第三象限角，f(x)＝＋＋＝－1.‎ 若x为第四象限角，f(x)＝＋＋＝－1.‎ 故选D.‎ ‎3．(2020·河南省洛阳市高三统考)已知角α的始边与x轴的非负半轴重合，顶点与坐标原点重合，终边过点P(3,4)，则＝(　A　)‎ A．10　 B．　‎ C．5　 D． ‎[解析]　根据角α的终边过P(3,4)，利用三角函数的定义，得tan α＝，所以有＝＝＝＝10.故选A.‎ ‎4．(2020·广东广州花都模拟)《九章算术》是我国古代数学成就的杰出代表，是《算经十书》中最重要的一种，其中《方田》章有弧田面积计算问题，计算术曰：以弦乘矢，矢又自乘，并之，二而一．其大意是，弧田面积的计算公式为弧田面积＝(弦×矢＋矢×矢)．弧田是由圆弧(简称为弧田弧)和以圆弧的端点为端点的线段(简称为弧田弦)围成的平面图形，公式中“弦”指的是弧田弦的长，“矢”等于弧田弧所在圆的半径与圆心到弧田弦的距离之差．现有一弧田，其弦长AB等于‎6 m，其弧所在圆为圆O，若用上述弧田面积计算公式算得该弧田的面积为 m2，则cos∠AOB＝(　D　)‎ A．　 B．　‎ C．　 D． ‎[解析]　设矢为x m，则由弧田面积公式得＝(6x＋x2)，解得x＝1或x＝－7(舍去)，设圆O的半径为R m，则R2＝(R－1)2＋32，解得R＝5，则cos∠AOB＝＝，故选D.‎ ‎5．已知sin α>sin β，那么下列命题成立的是(　D　)‎ A．若α，β是第一象限的角，则cos α>cos β B．若α，β是第二象限的角，则tan α>tan β C．若α，β是第三象限的角，则cos α>cos β - 6 -‎ D．若α，β是第四象限的角，则tan α>tan β ‎[解析]　分别作出选项A，B，C，D中角α.β的正弦线，如下图所示，由图可知选D.‎ - 6 -‎