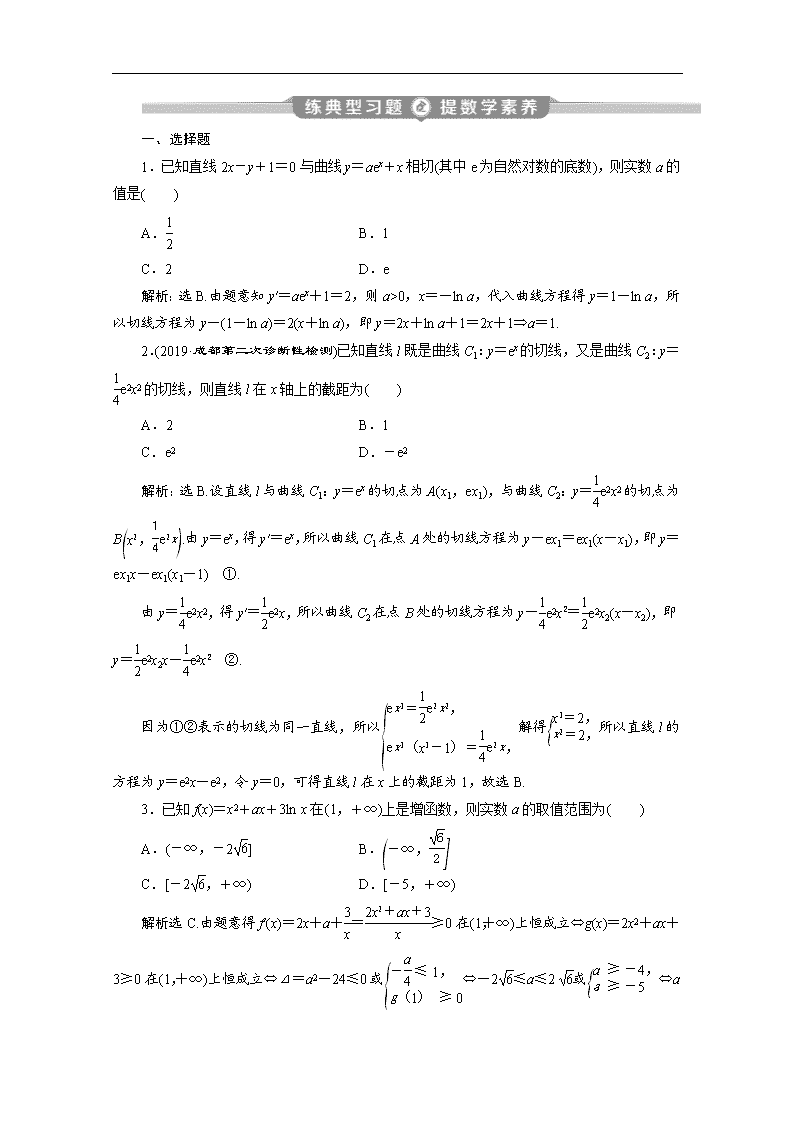2020高考数学二轮复习练习：第二部分 专题六 第3讲 导数的简单应用 练典型习题 提数学素养含解析 5页

一、选择题 ‎1．已知直线2x－y＋1＝0与曲线y＝aex＋x相切(其中e为自然对数的底数)，则实数a的值是(　　)‎ A．　　　　　　　 B．1‎ C．2 D．e 解析：选B.由题意知y′＝aex＋1＝2，则a>0，x＝－ln a，代入曲线方程得y＝1－ln a，所以切线方程为y－(1－ln a)＝2(x＋ln a)，即y＝2x＋ln a＋1＝2x＋1⇒a＝1.‎ ‎2．(2019·成都第二次诊断性检测)已知直线l既是曲线C1：y＝ex的切线，又是曲线C2：y＝e2x2的切线，则直线l在x轴上的截距为(　　)‎ A．2 B．1‎ C．e2 D．－e2‎ 解析：选B.设直线l与曲线C1：y＝ex的切点为A(x1，ex1)，与曲线C2：y＝e2x2的切点为B.由y＝ex，得y′＝ex，所以曲线C1在点A处的切线方程为y－ex1＝ex1(x－x1)，即y＝ex1x－ex1(x1－1)　①.‎ 由y＝e2x2，得y′＝e2x，所以曲线C2在点B处的切线方程为y－e2x＝e2x2(x－x2)，即y＝e2x2x－e2x　②.‎ 因为①②表示的切线为同一直线，所以解得所以直线l的方程为y＝e2x－e2，令y＝0，可得直线l在x上的截距为1，故选B.‎ ‎3．已知f(x)＝x2＋ax＋3ln x在(1，＋∞)上是增函数，则实数a的取值范围为(　　)‎ A．(－∞，－2] B． C．[－2，＋∞) D．[－5，＋∞)‎ 解析：选C.由题意得f′(x)＝2x＋a＋＝≥0在(1，＋∞)上恒成立⇔g(x)＝2x2＋ax＋3≥0在(1，＋∞)上恒成立⇔Δ＝a2－24≤0或⇔－2≤a≤2或⇔a≥－2，故选C.‎ ‎4．函数f(x)(x>0)的导函数为f′(x)，若xf′(x)＋f(x)＝ex，且f(1)＝e，则(　　)‎ A．f(x)的最小值为e B．f(x)的最大值为e C．f(x)的最小值为 D．f(x)的最大值为 解析：选A.设g(x)＝xf(x)－ex，‎ 所以g′(x)＝f(x)＋xf′(x)－ex＝0，‎ 所以g(x)＝xf(x)－ex为常数函数．‎ 因为g(1)＝1×f(1)－e＝0，‎ 所以g(x)＝xf(x)－ex＝g(1)＝0，‎ 所以f(x)＝，f′(x)＝，‎ 当01时，f′(x)>0，‎ 所以f(x)≥f(1)＝e.‎ ‎5．若函数f(x)＝ex－(m＋1)ln x＋2(m＋1)x－1恰有两个极值点，则实数m的取值范围为(　　)‎ A．(－e2，－e) B． C． D．(－∞，－e－1)‎ 解析：选D.由题意，函数的定义域为(0，＋∞)，f′(x)＝ex－(m＋1)＝0在(0，＋∞)上有两个不相等的实数根，所以m＋1＝在(0，＋∞)上有两个不相等的实数根，令g(x)＝，则g′(x)＝，所以函数g(x)在，上单调递增，在(1，＋∞)上单调递减，其图象如图所示，要使m＋1＝在(0，＋∞)上有两个不相等的实数根，则m＋12eπ 解析：选AC.由函数f(x)＝，可得函数f(x)的导数为f′(x)＝.当x>1时，f′(x)<0，f(x)单调递减；当x<1时，f′(x)>0，f(x)单调递增．可得函数f(x)在x＝1处取得极大值，且为最大值，所以A正确；因为f(x)在(－∞，1)上单调递增，在(1，＋∞)上单调递减，且f(0)＝0，当x>0时，f(x)>0恒成立，所以函数f(x)只有一个零点，所以B错误；由f(x)在(1，＋∞)上单调递减，且4>π>3>1，可得f(4)2>1，可得<，即πe2<2eπ，所以D错误．故选AC.‎ 二、填空题 ‎7．(2019·高考全国卷Ⅰ)曲线y＝3(x2＋x)ex在点(0，0)处的切线方程为________．‎ 解析：因为y′＝3(2x＋1)ex＋3(x2＋x)ex＝3(x2＋3x＋1)ex，所以曲线在点(0，0)处的切线的斜率k＝y′|x＝0＝3，所以所求的切线方程为y＝3x.‎ 答案：y＝3x ‎8．函数f(x)＝x2－ln x的最小值为________．‎ 解析：因为f(x)＝x2－ln x(x>0)，所以f′(x)＝2x－，令2x－＝0得x＝，令f′(x)>0，则x>；令f′(x)<0，则01时，f′(x)>0，此时函数f(x)为增函数，当－20，‎ ‎①当a≤0时，显然f′(x)>0，所以f(x)在(0，＋∞)上单调递增；‎ ‎②当a>0时，令f′(x)＝＝0，则－2ax2＋x＋1＝0，易知其判别式为正，‎ 设方程的两根分别为x1，x2(x10.‎ 令f′(x)>0，得x∈(0，x2)，令f′(x)<0得x∈(x2，＋∞)，其中x2＝.‎ 所以函数f(x)在上单调递增，‎ 在上单调递减．‎ ‎11．已知常数a≠0，f(x)＝aln x＋2x.‎ ‎(1)当a＝－4时，求f(x)的极值；‎ ‎(2)当f(x)的最小值不小于－a时，求实数a的取值范围．‎ 解：(1)由已知得f(x)的定义域为(0，＋∞)，‎ f′(x)＝＋2＝.‎ 当a＝－4时，f′(x)＝.‎ 所以当02时，f′(x)>0，即f(x)单调递增．‎ 所以f(x)只有极小值，且在x＝2时，f(x)取得极小值f(2)＝4－4ln 2.‎ 所以当a＝－4时，f(x)只有极小值4－4ln 2.‎ ‎(2)因为f′(x)＝，‎ 所以当a>0，x∈(0，＋∞)时，f′(x)>0，‎ 即f(x)在x∈(0，＋∞)上单调递增，没有最小值；‎ 当a<0时，由f′(x)>0得，x>－，‎ 所以f(x)在上单调递增；‎ 由f′(x)<0得，x<－，‎ 所以f(x)在上单调递减．‎ 所以当a<0时，f(x)的最小值为极小值，即f＝aln－a.‎ 根据题意得f＝aln－a≥－a，‎ 即a[ln(－a)－ln 2]≥0.‎ 因为a<0，所以ln(－a)－ln 2≤0，解得a≥－2，‎ 综上实数a的取值范围是[－2，0)．‎ ‎12．(2019·广州市调研测试)已知函数f(x)＝xex＋a(ln x＋x)．‎ ‎(1)若a＝－e，求f(x)的单调区间；‎ ‎(2)当a<0时，记f(x)的最小值为m，求证：m≤1.‎ 解：(1)当a＝－e时，f(x)＝xex－e(ln x＋x)，f(x)的定义域是(0，＋∞)．‎ f′(x)＝(x＋1)ex－e＝(xex－e)．‎ 当01时．f′(x)>0.‎ 所以函数f(x)的单调递减区间为(0，1)，单调递增区间为(1，＋∞)．‎ ‎(2)证明：f(x)的定义域是(0，＋∞)，f′(x)＝(xex＋a)，‎ 令g(x)＝xex＋a，则g′(x)＝(x＋1)ex>0，g(x)在(0，＋∞)上单调递增．‎ 因为a<0，所以g(0)＝a<0，g(－a)＝－ae－a＋a>－a＋a＝0，‎ 故存在x0∈(0，－a)，使得g(x0)＝x0ex0＋a＝0.‎ 当x∈(0，x0)时，g(x)<0，f′(x)＝(xex＋a)<0，f(x)单调递减；‎ 当x∈(x0，＋∞)时，g(x)>0，f′(x)＝(xex＋a)>0，f(x)单调递增．‎ 故x＝x0时，f(x)取得最小值，即m＝f(x0)＝x0ex0＋a(ln x0＋x0)．‎ 由x0ex0＋a＝0得m＝x0ex0＋a ln(x0ex0)＝－a＋a ln(－a)，‎ 令x＝－a>0，h(x)＝x－x ln x，则h′(x)＝1－(1＋ln x)＝－ln x，‎ 当x∈(0，1)时，h′(x)＝－ln x>0，h(x)＝x－xln x单调递增，‎ 当x∈(1，＋∞)时，h′(x)＝－ln x<0，h(x)＝x－xln x单调递减，‎ 故x＝1，即a＝－1时，h(x)＝x－x ln x取得最大值1，故m≤1.‎ ‎ ‎