2020高中数学第二章函数第5节指数与指数函数课时作业1北师大版必修1 9页

第5节 指数与指数函数 课时作业 A组——基础对点练 ‎1．函数f(x)＝2|x－1|的大致图像是(　　)‎ 解析：f(x)＝所以f(x)的图像在[1，＋∞)上为增函数，在(－∞，1)上为减函数．‎ 答案：B ‎2．(2018·广州市模拟)设a＝0.70.4，b＝‎0.40.7‎，c＝0.40.4，则a，b，c的大小关系为(　　)‎ A．b＜a＜c　　　　　　 B．a＜c＜b C．b＜c＜a D．c＜b＜a 解析：∵函数y＝0.4x在R上单调递减，∴‎0.40.7‎＜0.40.4，即b＜c，∵y＝x0.4在(0，＋∞)上单调递增，∴0.40.4＜0.70.4，即c＜a，∴b＜c＜a.‎ 答案：C ‎3．设a>0，将表示成分数指数幂的形式，其结果是(　　)‎ A．a B．a C．a D．a 解析：＝＝＝＝a2－＝a.故选C.‎ 答案：C ‎4．设x>0，且10，∴b>1，‎ ‎∵bx1，∵x>0，∴>1⇒a>b，∴10，且a≠1，如果以P(x1，f(x1))，Q(x2，f(x2))为端点的线段的中点在y轴上，那么f(x1)·f(x2)等于(　　)‎ 9‎ A．1 B．a C．2 D．a2‎ 解析：∵以P(x1，f(x1))，Q(x2，f(x2))为端点的线段的中点在y轴上，‎ ‎∴x1＋x2＝0.‎ 又∵f(x)＝ax，‎ ‎∴f(x1)·f(x2)＝ax1·ax2＝ax1＋x2＝a0＝1，故选A.‎ 答案：A ‎6．已知a＝，b＝，c＝，则(　　)‎ A．a，∴b，‎ ‎∴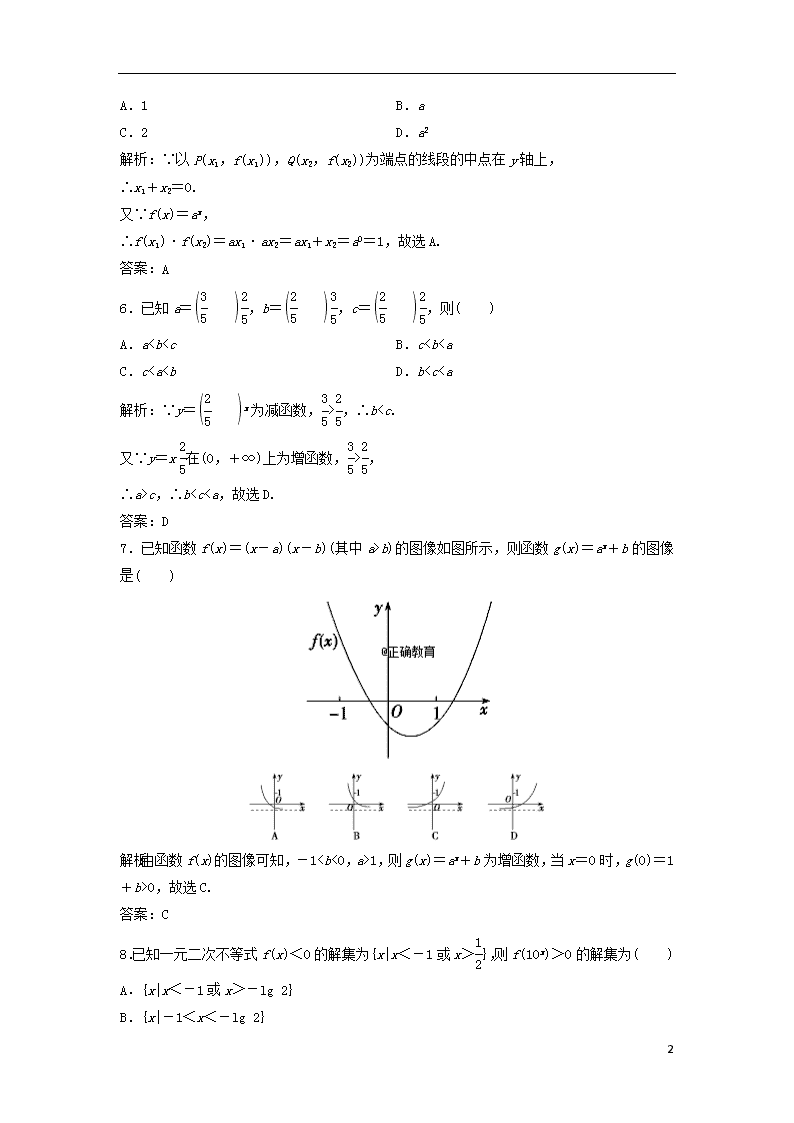a>c，∴bb)的图像如图所示，则函数g(x)＝ax＋b的图像是(　　)‎ 解析：由函数f(x)的图像可知，－11，则g(x)＝ax＋b为增函数，当x＝0时，g(0)＝1＋b>0，故选C.‎ 答案：C ‎8．已知一元二次不等式f(x)＜0的解集为{x|x＜－1或x＞}，则f(10x)＞0的解集为(　　)‎ A．{x|x＜－1或x＞－lg 2}‎ B．{x|－1＜x＜－lg 2}‎ 9‎ C．{x|x＞－lg 2}‎ D．{x|x＜－lg 2}‎ 解析：因为一元二次不等式f(x)＜0的解集为，所以可设f(x)＝a(x＋1)·(a＜0)，由f(10x)＞0可得(10x＋1)·＜0，即10x＜，x＜－lg 2，故选D.‎ 答案：D ‎9．函数y＝2x－x2的值域为(　　)‎ A. B. C. D．(0,2]‎ 解析：∵2x－x2＝－(x－1)2＋1≤1，‎ 又y＝t在R上为减函数，‎ ‎∴y＝2x－x2≥1＝，‎ 即值域为.‎ 答案：A ‎10．(2018·哈尔滨模拟)函数f(x)＝的图像(　　)‎ A．关于原点对称 B．关于直线y＝x对称 C．关于x轴对称 D．关于y轴对称 解析：f(x)＝＝ex＋，∵f(－x)＝e－x＋＝ex＋＝f(x)，∴f(x)是偶函数，∴函数f(x)的图像关于y轴对称．‎ 答案：D ‎11．(2018·北京丰台模拟)已知奇函数y＝如果f(x)＝ax(a＞0，且a≠1)对应的图像如图所示，那么g(x)＝(　　)‎ A.－x B．－x C．2－x D．－2x 9‎ 解析：由题图知f(1)＝，∴a＝，f(x)＝x，‎ 由题意得g(x)＝－f(－x)＝－－x＝－2x，故选D.‎ 答案：D ‎12．关于x的方程x＝有负数根，则实数a的取值范围为________．‎ 解析：由题意，得x＜0，所以0＜x＜1，‎ 从而0＜＜1，解得－＜a＜.‎ 答案： ‎13．不等式2x2－x＜4的解集为________．‎ 解析：不等式2x2－x＜4可转化为2x2－x＜22，利用指数函数y＝2x的性质可得，x2－x＜2，解得－1＜x＜2，故所求解集为{x|－1＜x＜2}．‎ 答案：{x|－1＜x＜2}‎ ‎14．已知y＝f(x)是定义在R上的奇函数，且当x≥0时，f(x)＝－＋，则此函数的值域为________．‎ 解析：设t＝，当x≥0时，2x≥1，∴0＜t≤1，f(t)＝－t2＋t＝－2＋，∴0≤f(t)≤，故当x≥0时，f(x)∈.∵y＝f(x)是定义在R上的奇函数，∴当x≤0时，f(x)∈.故函数的值域为.‎ 答案： B组——能力提升练 ‎1．设函数f(x)定义在实数集上，它的图像关于直线x＝1对称，且当x≥1时，f(x)＝3x－1，则有(　　)‎ A．f＜f＜f B．f＜f＜f C．f＜f＜f D．f＜f＜f 9‎ 解析：∵函数f(x)的图像关于直线x＝1对称，‎ ‎∴f(x)＝f(2－x)，∴f＝f＝f，f＝f＝f，又∵x≥1时，f(x)＝3x－1为单调递增函数，且＜＜，‎ ‎∴f＜f＜f，‎ 即f＜f＜f.选B.‎ 答案：B ‎2．已知实数a，b满足等式2 ‎017a＝2 018b，下列五个关系式：①01，则有a>b>0；若t＝1，则有a＝b＝0；若00，且a≠1)的图像可能是(　　)‎ 解析：函数y＝ax－是由函数y＝ax的图像向下平移个单位长度得到，A项显然错误；当a>1时，0<<1，平移距离小于1，所以B项错误；当01，平移距离大于1，所以C项错误，故选D.‎ 答案：D ‎4．(2018·日照模拟)若x∈(2,4)，a＝2x2，b＝(2x)2，c＝22x，则a，b，c的大小关系是(　　)‎ 9‎ A．a>b>c B．a>c>b C．c>a>b D．b>a>c 解析：∵b＝(2x)2＝22x，∴要比较a，b，c的大小，只要比较当x∈(2,4)时x2,2x,2x的大小即可．用特殊值法，取x＝3，容易知x2>2x>2x，则a>c>b.‎ 答案：B ‎5．已知a＞0，且a≠1，f(x)＝x2－ax.当x∈(－1,1)时，均有f(x)＜，则实数a的取值范围是(　　)‎ A.∪[2，＋∞) B.∪(1,2]‎ C.∪[4，＋∞) D.∪(1,4]‎ 解析：当x∈(－1,1)时，均有f(x)＜，即ax＞x2－在(－1,1)上恒成立，‎ 令g (x)＝ax，m(x)＝x2－，当0＜a＜1时，g(1)≥m(1)，即a≥1－＝，此时≤a＜1；‎ 当a＞1时，g(－1)≥m(1)，即a－1≥1－＝，此时1＜a≤2.‎ 综上，≤a＜1或1＜a≤2.故选B.‎ 答案：B ‎6．(2018·菏泽模拟)若函数f(x)＝1＋＋sin x在区间[－ ， ]( ＞0)上的值域为[m，n]，则m＋n的值是(　　)‎ A．0 B．1‎ C．2 D．4‎ 解析：∵f(x)＝1＋＋sin x ‎＝1＋2·＋sin x ‎＝2＋1－＋sin x ‎＝2＋＋sin x.‎ 记g(x)＝＋sin x，则f(x)＝g(x)＋2，‎ 易知g(x)为奇函数，则g(x)在[－ ， ]上的最大值与最小值互为相反数，∴m＋n＝4.‎ 答案：D ‎7．若xlog52≥－1，则函数f(x)＝4x－2x＋1－3的最小值为(　　)‎ 9‎ A．－4 B．－3‎ C．－1 D．0‎ 解析：∵xlog52≥－1，∴2x≥，则f(x)＝4x－2x＋1－3＝(2x)2－2×2x－3＝(2x－1)2－4.当2x＝1时，f(x)取得最小值－4.‎ 答案：A ‎8．若x＞1，y＞0，xy＋x－y＝2，则xy－x－y的值为(　　)‎ A. B．－2‎ C．2 D．2或－2‎ 解析：∵x＞1，y＞0，∴xy＞1,0＜x－y＜1，则xy－x－y＞0.‎ ‎∵xy＋x－y＝2，∴x2y＋2xy·x－y＋x－2y＝8，即x2y＋x－2y＝6，∴(xy－x－y)2＝4，从而xy－x－y＝2，故选C.‎ 答案：C ‎9．已知实数a，b满足＞a＞b＞，则(　　)‎ A．b＜2 B．b＞2 C．a＜ D．a＞ 解析：由＞a，得a＞1；‎ 由a＞b，得‎2a＞b，进而‎2a＜b；‎ 由b＞，得b＞4，进而b＜4.‎ ‎∴1＜a＜2,2＜b＜4.‎ 取a＝，b＝，得＝＝，有a＞，排除C；b＞2，排除A；‎ 取a＝，b＝，得＝＝，有a＜，排除D.故选B.‎ 答案：B ‎10．已知函数f(x)＝·x，m，n为实数，则下列结论中正确的是(　　)‎ A．若－3≤m＜n，则f(m)＜f(n)‎ B．若m＜n≤0，则f(m)＜f(n)‎ C．若f(m)＜f(n)，则m2＜n2‎ D．若f(m)＜f(n)，则m3＜n3‎ 解析：∵f(x)的定义域为R，其定义域关于原点对称，f(－x)＝·(－x)＝ 9‎ ‎·x＝f(x)，∴函数f(x)是一个偶函数，又x＞0时，2x－与x是增函数，且函数值为正，∴函数f(x)＝·x在(0，＋∞)上是一个增函数，由偶函数的性质知，函数f(x)在(－∞，0)上是一个减函数，此类函数的规律是：自变量离原点越近，函数值越小，即自变量的绝对值越小，函数值就越小，反之也成立．对于选项A，无法判断m，n离原点的远近，故A错误；对于选项B，|m|＞|n|，∴f(m)＞f(n)，故B错误；对于选项C，由f(m)＜f(n)，一定可得出m2＜n2，故C是正确的；对于选项D，由f(m)＜f(n)，可得出|m|＜|n|，但不能得出m3＜n3，故D错误．综上可知，选C.‎ 答案：C ‎11．(2017·高考全国卷Ⅲ)已知函数f(x)＝x2－2x＋a(ex－1＋e－x＋1)有唯一零点，则a＝(　　)‎ A．－ B. C. D．1‎ 解析：由f(x)＝x2－2x＋a(ex－1＋e－x＋1)，得 f(2－x)＝(2－x)2－2(2－x)＋a[e2－x－1＋e－(2－x)＋1]＝x2－4x＋4－4＋2x＋a(e1－x＋ex－1)＝x2－2x＋a(ex－1＋e－x＋1)，所以f(2－x)＝f(x)，即x＝1为f(x)图像的对称轴．‎ 由题意，f(x)有唯一零点，所以f(x)的零点只能为x＝1，即f(1)＝12－2×1＋a(e1－1＋e－1＋1)＝0，‎ 解得a＝.故选C.‎ 答案：C ‎12．若函数f(x)＝2|x－a|(a∈R)满足f(1＋x)＝f(1－x)，且f(x)在[m，＋∞)上单调递增，则实数m的最小值等于________．‎ 解析：因为f(1＋x)＝f(1－x)，所以函数f(x)关于直线x＝1对称，所以a＝1，所以函数f(x)＝2|x－1|的图像如图所示，因为函数f(x)在[m，＋∞)上单调递增，所以m≥1，所以实数m的最小值为1.‎ 答案：1‎ ‎13．(2018·眉山模拟)已知定义在R上的函数g(x)＝2x＋2－x＋|x|，则满足g(2x－1)＜g(3)的x的取值范围是________．‎ 9‎ 解析：∵g(x)＝2x＋2－x＋|x|，∴g(－x)＝2x＋2－x＋|－x|,2x＋2－x＋|x|＝g(x)，则函数g(x)为偶函数，当x≥0时，g(x)＝2x＋2－x＋x，则g′(x)＝(2x－2－x)·ln 2＋1＞0，则函数g(x)在[0，＋∞)上为增函数，而不等式g(2x－1)＜g(3)等价于g(|2x－1|)＜g(3)，∴|2x－1|＜3，即－3＜2x－1＜3，解得－1＜x＜2，即x的取值范围是(－1,2)．‎ 答案：(－1,2)‎ ‎14．(2018·信阳质检)若不等式(m2－m)2x－x＜1对一切x∈(－∞，－1]恒成立，则实数m的取值范围是________．‎ 解析：(m2－m)2x－x＜1可变形为m2－m＜x＋2，设t＝x，则原条件等价于不等式m2－m＜t＋t2在t≥2时恒成立，显然t＋t2在t≥2时的最小值为6，所以m2－m＜6，解得－2＜m＜3.‎ 答案：(－2,3)‎ 9‎