2020高中数学 第三章 第1课时 一元二次不等式及其解法学案 新人教A版必修5 8页

第1课时　一元二次不等式及其解法 学习目标：1.掌握一元二次不等式的解法(重点).2.能根据“三个二次”之间的关系解决简单问题(难点)．‎ ‎[自 主 预 习·探 新 知]‎ ‎1．一元二次不等式的概念 只含有一个未知数，并且未知数的最高次数是2的不等式，称为一元二次不等式．‎ ‎2．一元二次不等式的一般形式 ‎(1)ax2＋bx＋c＞0(a≠0)．‎ ‎(2)ax2＋bx＋c≥0(a≠0)．‎ ‎(3)ax2＋bx＋c＜0(a≠0)．‎ ‎(4)ax2＋bx＋c≤0(a≠0)．‎ 思考：不等式x2－y2>0是一元二次不等式吗？‎ ‎[提示]　此不等式含有两个变量，根据一元二次不等式的定义，可知不是一元二次不等式．‎ ‎3．一元二次不等式的解与解集 使一元二次不等式成立的未知数的值，叫做这个一元二次不等式的解，其解的集合，称为这个一元二次不等式的解集．‎ 思考：类比“方程x2＝1的解集是{1，－1}，解集中的每一个元素均可使等式成立”．不等式x2>1的解集及其含义是什么？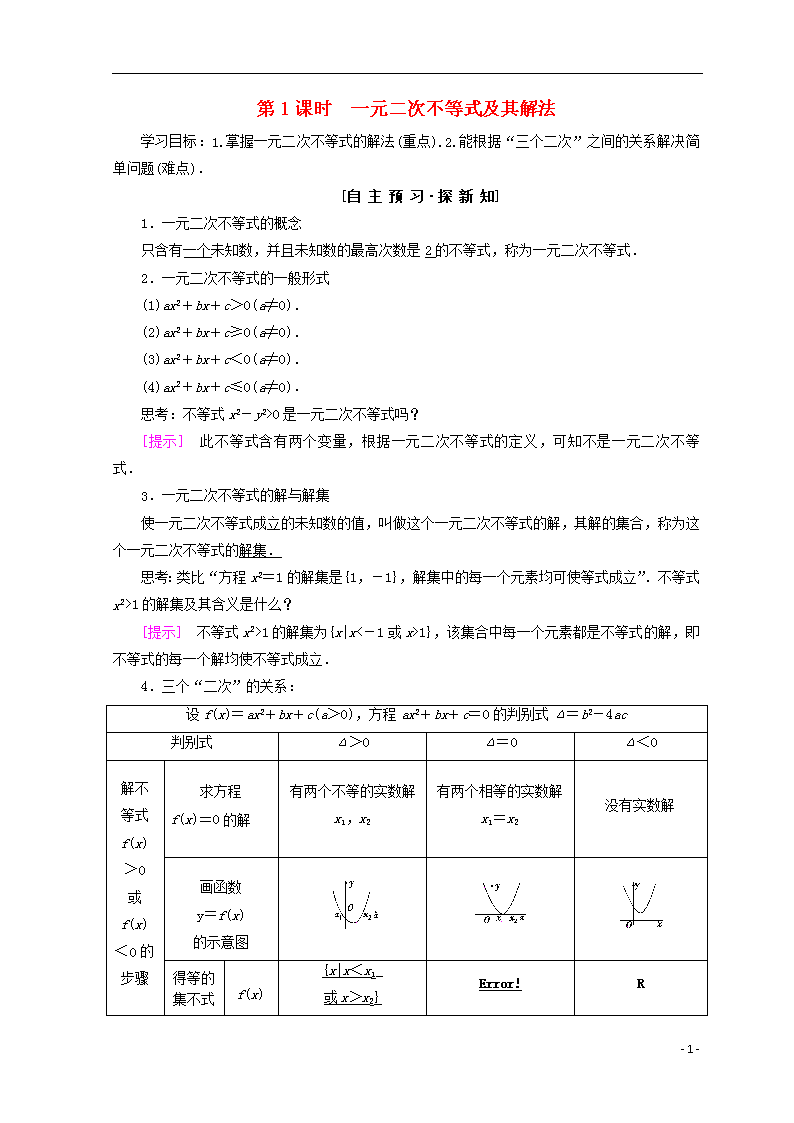‎ ‎[提示]　不等式x2>1的解集为{x|x<－1或x>1}，该集合中每一个元素都是不等式的解，即不等式的每一个解均使不等式成立．‎ ‎4．三个“二次”的关系：‎ 设f(x)＝ax2＋bx＋c(a＞0)，方程ax2＋bx＋c＝0的判别式Δ＝b2－‎‎4ac 判别式 Δ＞0‎ Δ＝0‎ Δ＜0‎ 解不 等式 f(x)‎ ‎＞0‎ 或 f(x)‎ ‎＜0的 步骤 求方程 f(x)＝0的解 有两个不等的实数解 x1，x2‎ 有两个相等的实数解 x1＝x2‎ 没有实数解 画函数 y＝f(x)‎ 的示意图 f(x)‎ ‎{x|x＜x1_‎ 或x＞x2}‎ R - 8 -‎ 得等的集不式解 ‎＞0‎ f(x)‎ ‎＜0‎ ‎{x|x1＜‎ x＜x2}‎ ‎∅‎ ‎∅‎ 思考：若一元二次不等式ax2＋x－1>0的解集为R，则实数a应满足什么条件？‎ ‎[提示]　结合二次函数图象可知，若一元二次不等式ax2＋x－1>0的解集为R，则解得a∈∅，所以不存在a使不等式ax2＋x－1>0的解集为R.‎ ‎[基础自测]‎ ‎1．思考辨析 ‎(1)mx2－5x<0是一元二次不等式．(　　)‎ ‎(2)若a>0，则一元二次不等式ax2＋1>0无解．(　　)‎ ‎(3)若一元二次方程ax2＋bx＋c＝0的两根为x1，x2(x10的解集为R.(　　)‎ ‎[答案]　(1)×　(2)×　(3)×　(4)√　‎ 提示：(1)错误．当m＝0时，是一元一次不等式；当m≠0时，是一元二次不等式．(2)错误．因为a>0，所以不等式ax2＋1>0恒成立，即原不等式的解集为R.(3)错误．当a>0时，ax2＋bx＋c<0的解集为{x|x10的解集为R.‎ ‎2．(2018·全国卷Ⅰ)已知集合A＝{x|x2－x－2＞0}，则∁RA＝(　　)‎ A．{x|－1＜x＜2}　　　　　 B．{x|－1≤x≤2}‎ C．{x|x＜－1}∪{x|x＞2} D．{x|x≤－1}∪{x|x≥2}‎ B　[通解　A＝{x|(x－2)(x＋1)＞0}＝{x|x＜－1或x＞2}，所以∁RA＝{x|－1≤x≤2}，故选B.‎ 优解　因为A＝{x|x2－x－2＞0}，所以∁RA＝{x|x2－x－2≤0}＝{x|－1≤x≤2}，故选B.]‎ ‎3．不等式x2－2x－5>2x的解集是________．‎ ‎{x|x>5或x<－1}　[由x2－2x－5>2x，得x2－4x－5>0，‎ 因为x2－4x－5＝0的两根为－1,5，‎ 故x2－4x－5>0的解集为{x|x<－1或x>5}．]‎ ‎4．不等式－3x2＋5x－4>0的解集为________. ‎ ‎【导学号：91432278】‎ ‎∅　[原不等式变形为3x2－5x＋4<0.‎ 因为Δ＝(－5)2－4×3×4＝－23<0，所以3x2－5x＋4＝0无解．‎ 由函数y＝3x2－5x＋4的图象可知，3x2－5x＋4<0的解集为∅.]‎ ‎[合 作 探 究·攻 重 难]‎ - 8 -‎ 一元二次不等式的解法 ‎　解下列不等式：‎ ‎(1)2x2＋7x＋3>0；‎ ‎(2)－4x2＋18x－≥0；‎ ‎(3)－2x2＋3x－2<0.‎ ‎[解]　(1)因为Δ＝72－4×2×3＝25>0，所以方程2x2＋7x＋3＝0有两个不等实根x1＝－3，x2＝－.又二次函数y＝2x2＋7x＋3的图象开口向上，所以原不等式的解集为.‎ ‎(2)原不等式可化为2≤0，所以原不等式的解集为.‎ ‎(3)原不等式可化为2x2－3x＋2>0，因为Δ＝9－4×2×2＝－7<0，所以方程2x2－3x＋2＝0无实根，又二次函数y＝2x2－3x＋2的图象开口向上，所以原不等式的解集为R.‎ ‎[规律方法]　解不含参数的一元二次不等式的一般步骤 ‎(1)化标准.通过对不等式的变形，使不等式右侧为0，使二次项系数为正.‎ ‎(2)判别式.对不等式左侧因式分解，若不易分解，则计算对应方程的判别式.‎ ‎(3)求实根.求出相应的一元二次方程的根或根据判别式说明方程有无实根.‎ ‎(4)画草图.根据一元二次方程根的情况画出对应的二次函数的草图.‎ ‎(5)写解集.根据图象写出不等式的解集.‎ ‎ [跟踪训练]‎ ‎1．解下列不等式 ‎(1)2x2－3x－2>0；‎ ‎(2)x2－4x＋4>0；‎ ‎(3)－x2＋2x－3<0；‎ ‎(4)－3x2＋5x－2>0.‎ ‎【导学号：91432279】‎ ‎[解]　(1)∵Δ>0，方程2x2－3x－2＝0的根是x1＝－，x2＝2，‎ ‎∴不等式2x2－3x－2>0的解集为 .‎ ‎(2)∵Δ＝0，方程x2－4x＋4＝0的根是x1＝x2＝2，‎ ‎∴不等式x2－4x＋4>0的解集为.‎ ‎(3)原不等式可化为x2－2x＋3>0，‎ 由于Δ<0，方程x2－2x＋3＝0无解，‎ - 8 -‎ ‎∴不等式－x2＋2x－3<0的解集为R.‎ ‎(4)原不等式可化为3x2－5x＋2<0，‎ 由于Δ>0，方程3x2－5x＋2＝0的两根为x1＝，x2＝1，‎ ‎∴不等式－3x2＋5x－2>0的解集为.‎ 含参数的一元二次不等式的解法 ‎　解关于x的不等式ax2－(a＋1)x＋1<0.‎ 思路探究：①对于二次项的系数a是否分a＝0，a<0，a>0三类进行讨论？②当a≠0时，是否还要比较两根的大小？‎ ‎[解]　当a＝0时，原不等式可化为x>1.‎ 当a≠0时，原不等式可化为(ax－1)(x－1)<0.‎ 当a<0时，不等式可化为(x－1)>0，‎ ‎∵<1，∴x<或x>1.‎ 当a>0时，原不等式可化为(x－1)<0.‎ 若<1，即a>1，则1，即01}；当01时，原不等式的解集为.‎ ‎[规律方法]　‎ 解含参数的一元二次不等式的一般步骤 - 8 -‎ 注：对参数分类讨论的每一种情况是相互独立的一元二次不等式的解集，不能合并．‎ ‎[跟踪训练]‎ ‎2．解关于x的不等式：ax2－2≥2x－ax(a<0). 【导学号：91432280】‎ ‎[解]　原不等式移项得ax2＋(a－2)x－2≥0，‎ 化简为(x＋1)(ax－2)≥0.‎ ‎∵a<0，∴(x＋1)≤0.‎ 当－20、y<0、y＝0时x的取值集合分别是什么？这说明二次函数与二次方程、二次不等式有何关系？‎ 提示：y＝x2－2x－3的图象如图所示．‎ 函数y＝x2－2x－3的值满足y>0时自变量x组成的集合，亦即二次函数y＝x2－2x－3的图象在x轴上方时点的横坐标x的集合{x|x<－1或x>3}；同理，满足y<0时x的取值集合为{x|－10(a>0)或ax2＋bx＋c<0(a>0)是函数y＝ax2＋bx＋c(a≠0)的一种特殊情况，它们之间是一种包含关系，也就是当y＝0时，函数y＝ax2＋bx＋c(a≠0)就转化为方程，当y>0或y<0时，就转化为一元二次不等式．‎ ‎2．方程x2－2x－3＝0与不等式x2－2x - 8 -‎ ‎－3>0的解集分别是什么？观察结果你发现什么问题？这又说明什么？‎ 提示：方程x2－2x－3＝0的解集为{－1,3}．‎ 不等式x2－2x－3>0的解集为{x|x<－1或x>3}，观察发现不等式x2－2x－3>0解集的端点值恰好是方程x2－2x－3＝0的根．‎ ‎3．设一元二次不等式ax2＋bx＋c>0(a>0)和ax2＋bx＋c<0(a>0)的解集分别为{x|xx2}，{x|x10(a>0)和ax2＋bx＋c<0(a>0)的解集分别为{x|xx2}，{x|x10的解集为{x|20的解集为{x|20，即x2－x＋>0，解得x<或x>，所以不等式cx2＋bx＋a<0的解集为∪.‎ 法二：由不等式ax2＋bx＋c>0的解集为{x|20的解集．‎ ‎[解]　由根与系数的关系知＝－5，＝6且a<0.‎ ‎∴c<0，＝－，故不等式cx2－bx＋a>0‎ 即x2－x＋<0，即x2＋x＋<0.‎ 解之得.‎ ‎2．(变条件)若将本例中的条件“关于x的不等式ax2＋bx＋c>0的解集为{x|20，得(x－1)(2x＋1)>0，解得x>1或x<－，从而得原不等式的解集为∪(1，＋∞)．]‎ ‎3．设a<－1，则关于x的不等式a(x－a)<0的解集为________．‎ 　[因为a<－1，所以a(x－a)·<0⇔(x－a)·>0.又a<－1，所以>a，所以x>或x0的解集为________．‎ 　[由题意，－2，－是方程ax2＋bx＋c＝0的两个根且a<0，‎ 故解得a＝c，b＝c.‎ 所以不等式ax2－bx＋c>0即为2x2－5x＋2<0，‎ 解得0的解集为.]‎ ‎5．解下列不等式：‎ ‎(1)x(7－x)≥12；‎ ‎(2)x2>2(x－1).‎ ‎【导学号：91432283】‎ ‎[解]　(1)原不等式可化为x2－7x＋12≤0，因为方程x2－7x＋12＝0的两根为x1＝3，x2＝4，‎ 所以原不等式的解集为{x|3≤x≤4}．‎ ‎(2)原不等式可以化为x2－2x＋2>0，‎ 因为判别式Δ＝4－8＝－4<0，方程x2－2x＋2＝0无实根，而抛物线y＝x2－2x＋2的图象开口向上，‎ 所以原不等式的解集为R.‎ - 8 -‎