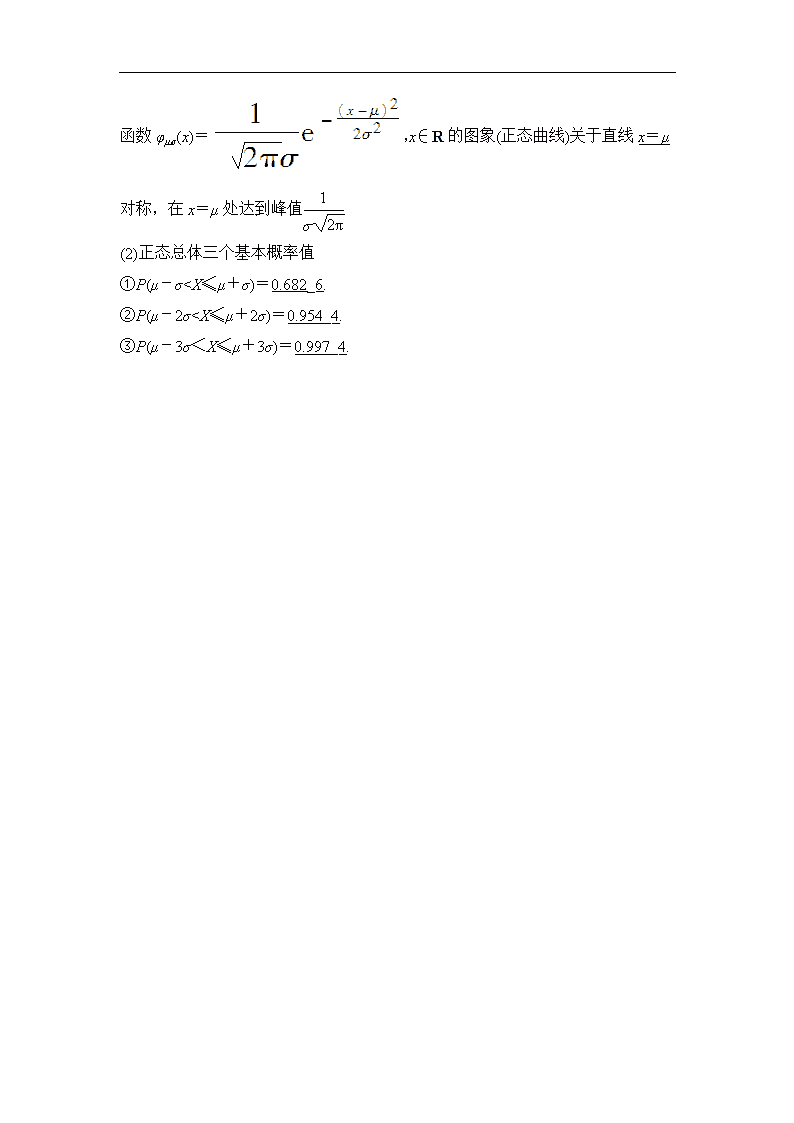高考数学专题复习教案： 条件概率与独立事件、二项分布、正态分布 3页

条件概率与独立事件、二项分布、正态分布 主标题：条件概率与独立事件、二项分布、正态分布 副标题：为学生详细的分析条件概率与独立事件、二项分布、正态分布的高考考点、命题方向以及规律总结。‎ 关键词：条件概率，独立事件，二项分布，正态分布 难度：3‎ 重要程度：4‎ 考点剖析：‎ ‎1．了解条件概率和两个事件相互独立的概念．‎ ‎2．理解n次独立重复试验的模型及二项分布．‎ ‎3．能解决一些简单的实际问题.‎ 命题方向：‎ ‎ 1．独立重复试验与二项分布是高中数学的重要内容，也是高考命题的热点，多以解答题的形式呈现，试题难度较大，多为中高档题目．‎ ‎2．高考对独立重复试验与二项分布的考查主要有以下几个命题角度：‎ ‎(1)已知二项分布，求二项分布列；‎ ‎(2)已知随机变量服从二项分布，求某种情况下的概率．‎ 规律总结：‎ ‎1个难点——对正态曲线的理解 正态曲线指的是一个函数的图象，其函数解析式是φμ，σ(x)＝·e－.正态曲线的性质告诉我们：‎ ‎(1)该函数的值域为正实数集的子集；‎ ‎(2)该函数图象关于直线x＝μ对称，且以x轴为渐近线；‎ ‎(3)解析式中前面有一个系数，后面是一个以e为底数的指数函数的形式，幂指数为－，其中σ这个参数在解析式中的两个位置上出现，注意两者的一致性．‎ ‎2个注意点——掌握离散型随机变量分布列的注意点 ‎　(1)分布列的结构为两行，第一行为随机变量的所有可能取得的值；第二行为对应于随机变量取值的事件发生的概率．看每一列，实际上是：上为“事件”，下为“事件”发生的概率；‎ ‎ (2)要会根据分布列的两个性质来检验求得的分布列的正误．‎ 3种方法——求分布列的三种方法 ‎　(1)由统计数据得到离散型随机变量的分布列；‎ ‎(2)由古典概型求出离散型随机变量的分布列；‎ ‎(3)由互斥事件的概率、相互独立事件同时发生的概率及n次独立重复试验有k次发生的概率求离散型随机变量的分布列．‎ 知 识 梳 理 ‎1．条件概率及其性质 条件概率的定义 条件概率的性质 设A，B为两个事件，且P(A)>0，称P(B|A)＝为在事件A发生的条件下，事件B发生的条件概率 ‎(1)0≤P(B|A)≤1‎ ‎(2)若B，C是两个互斥事件，则P(B∪C|A)＝P(B|A)＋P(C|A)‎ ‎2.事件的相互独立性 设A，B为两个事件，如果P(AB)＝P(A)P(B)，则称事件A与事件B相互独立．‎ 若事件A，B相互独立，则P(B|A)＝P(B)；事件A与，与B，与都相互独立．‎ ‎3．独立重复试验与二项分布 ‎(1)独立重复试验 在相同条件下重复做的n次试验称为n次独立重复试验，若用Ai(i＝1,2，…，n)表示第i次试验结果，则 P(A1A2A3…An)＝P(A1)P(A2)P(A3)…P(An)．‎ ‎(2)二项分布 在n次独立重复试验中，用X表示事件A发生的次数，设每次试验中事件A发生的概率为p，则P(X＝k)＝Cpk(1－p)n－k(k＝0,1,2，…，n)，此时称随机变量X服从二项分布，记为X～B(n，p)，并称p为成功概率．‎ ‎4．正态分布 ‎(1)正态分布的定义及表示 如果对于任何实数a，b(a