2018-2019学年湖北省黄冈市重点中学高一12月月考数学试卷 8页

‎2018-2019学年湖北省黄冈市重点中学高一12月月考数学试 ‎ 时间：120分钟 满分：150分 一、选择题（本大题共12小题，每小题5分，共60分）‎ 1. 集合A={y|y = + }， 则A的真子集有（　　）个．‎ A. 4 B. 6 C. 7 D. 8‎ ‎2.已知角θ的终边过点P（-4k，3k） （k＜0），则2sinθ+cosθ的值是（　　）‎ A. B. C. 或 D. 随k的值变化 ‎3.对于集合、，定义，．‎ 设，，则为( )‎ A. B. C. D. ‎ ‎4.若函数f（x）=单调递增，则实数a的取值范围是（　 ）‎ A. B. C. D. ‎ ‎5.已知扇形OAB的面积为1，周长为4，则弦AB的长度为（ ）‎ A.2 B. C. D. ‎ ‎6.已知lga+lgb=0，函数f（x）=ax与函数g（x）=-logbx的图象可能是（　　）‎ A. B. C. D. ‎ ‎7.已知是定义在R上的偶函数，它在上递减，那么一定有　　‎ A. B. C. D. ‎ ‎8.若函数f（x）=（m+2）xa是幂函数，且其图象过点（2，4），则函数g（x）=loga（x+m）的单调增区间为（　　）‎ A. B. C. D. ‎ 9. 已知奇函数的定义域为R，若为偶函数，且，则      ‎ A. B. C. 0 D. 1‎ 10. 设函数f（x）=alnx+blgx+1，则f（1）+f（2）+…+f（2014）+f（）+f（）+…+f（）=（　　）‎ A. ‎4028 B. 4027 C. 2014 D. 2013‎ 11. 直角坐标系内，角终边过点，则终边与重合的角可表示成（   ）‎ A. ‎ B. ‎ C. D.‎ 12. 设函数，若互不相等的实数x1，x2，x3满足f（x1）=f（x2）=f（x3），则x1+x2+x3的取值范围是（　　）‎ A. ‎ B. C. D. ‎ 二、填空题（本大题共4小题，共20分）‎ ‎13.若sinα是方程5x2－7x－6＝0的根，α是第三象限角，则·tan2(π－α)＝________‎ ‎14.函数f（x）= x- 的值域是______ ．‎ ‎15.已知函数f（x）＝|ax－1|－2a有两个零点，则实数a的取值范围是________．‎ ‎16.若，， 则的最大值是________.‎ 三、解答题（本大题共6小题，共70分.解答应写出文字说明或演算步骤）‎ ‎ ． （1）求A∩（∁RB）； （2）已知集合C={x|1＜x＜a}，若C∩A=C，求实数a的取值集合. 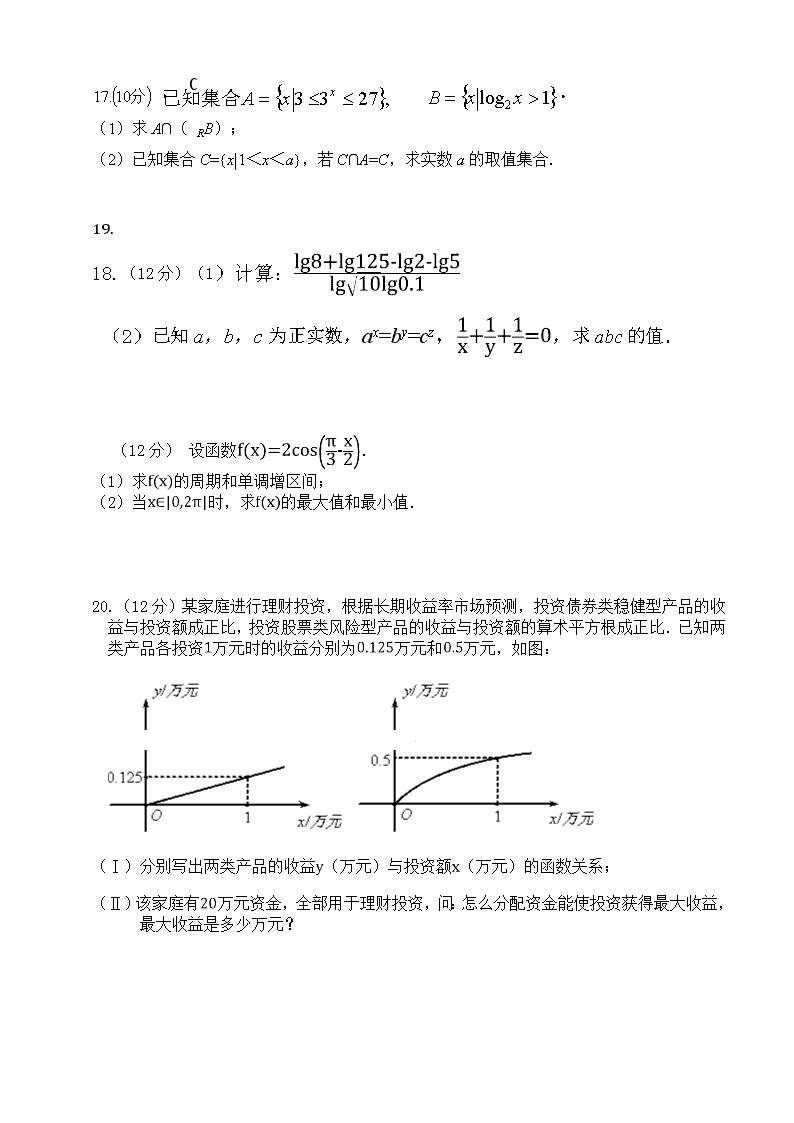‎ ‎ 18.（12分）（1）计算： （2）已知a，b，c为正实数，ax=by=cz，，求abc的值． 19.（12分） 设函数． （1）求的周期和单调增区间； （2）当时，求的最大值和最小值．‎ ‎20.（12分）某家庭进行理财投资，根据长期收益率市场预测，投资债券类稳健型产品的收益与投资额成正比，投资股票类风险型产品的收益与投资额的算术平方根成正比．已知两类产品各投资万元时的收益分别为万元和万元，如图：‎ ‎     ‎ ‎（Ⅰ）分别写出两类产品的收益（万元）与投资额（万元）的函数关系；‎ ‎（Ⅱ）该家庭有万元资金，全部用于理财投资，问：怎么分配资金能使投资获得最大收益，最大收益是多少万元？‎ ‎ ‎ ‎21.（12分）设f（x）=log - x 为奇函数，a为常数． （1）求a的值； （2）若对于区间[2，3]上的每一个x值，不等式f（x）＞2x+m恒成立，求实数m取值范围．‎ ‎ ‎ ‎22、（12分）对于函数，若在定义域内存在实数，满足，则称为“局部奇函数”‎ ‎（1）已知二次函数（且），试判断是否为“局部奇函数”，并说明理由；‎ ‎（2）若是定义在区间上的“局部奇函数”，求实数的取值范围；‎ ‎（3）若为定义域为上的“局部奇函数”，求实数的取值范围；‎ ‎2018年12月月考高一数学参考答案 一、选择题（本大题共12小题，每小题5分，共60分）‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ C B D B C B D A D B A B ‎10.【解析】解：∵=alnx+blgx+1+=2，f（1）=1， ∴f（1）+f（2）+…+f（2014）+f（）+f（）+…+f（） =1++…+ =1+2×2013 =4027．故选：B．‎ ‎11.【解析】解: 因为sin2>,cos2<0,‎ 所以P在第四象限,又,‎ 又为第四象限的角,所以终边与β重合的角可表示成, k∈Z.故选A. ‎ 12. ‎【解析】解：∵函数， ∴根据二次函数性质得出x2+x3=6，利用函数y=3x+4得出：x1=0时，x1+x2+x3＜6， y=（x-3）2-3，3x1+4=-3，x1=，∴x1+x2+x3＞+6=， ∴x1+x2+x3的取值范围是（，6），故选：B． ‎ 二．.填空题 （本大题共4题，每小题5分，共20分）‎ ‎ 14.（-∞，1] 15.（0，） 16. 13‎ ‎16.【解析】：∵f（x）=2+log3x，x∈[1，9]， ∴y=[f（x）]2+f（x2）=（2+log3x）2+（2+log3x2） =（log3x）2+6log3x+6，令t=log3x 由题意可得即1≤x≤3，则t∈[0，1] ∴y=t2+6t+6=（t+3）2-3在[0，1]上单调递增 当t=1即x=3时，函数有最大值，且ymax=13. ‎ 三.解答题 ‎17.解：（1）集合A={x|3≤3x≤27}={x|3≤3x≤33}={x|1≤x≤3}， B={x|log2x＞1}={x|log2x＞}={x|x＞2}， ∴∁R B={x|x≤2}，∴A∩（∁R B）={x|1≤x≤2}；........（5分）‎ ‎（2）∵C∩A=C，∴C⊆A， ①当a≤1时，C=∅，此时C⊆A； ②当a＞1时，集合C={x|1＜x＜a}，C⊆A，则1＜a≤3， 综上可得，实数a的取值集合是（-∞，3]． .........（10分）‎ ‎18.解:（1）原式= -4． ........ （6分）‎ ‎（ 2）∵a，b，c为正实数，ax=by=cz=k＞0，k≠1． ∴x=，y=，z=．∵，∴==0，‎ ‎∴abc=1 ..............（12分）‎ ‎19.解：函数，故它的周期为． ......（2分） 令，求得，‎ 故函数的增区间为． ......（6分） 当时，，，故当时，‎ 函数取得最小值为；当时，函数取得最大值2 ......（12分）‎ ‎20..解（Ⅰ）设 ，  ，所以  ，  ，‎ 即 ，   ........（4分） （Ⅱ）设投资债券类产品 万元，则股票类投资为 (  )万元， 依题意得：  ........（6分）   .......（10分） ，即  万元时，  万元 故投资债券类产品16万元、股票类4万元时，收益最大为3万元。 ........（12分）‎ 21. 解：（1）由条件得：f（-x）+f（x）=0，∴， 化简得（a2-1）x2=0，因此a2-1=0，a=±1， 当a=1时，，不符合题意，因此a=-1．   经检验，a=-1时，f(x)是奇函数 . ..........（4分）‎ ‎ （2） 依题知：不等式m＜f(x)-2x恒成立，∴m＜[f(x)-2x]min ... ..........（6分） ‎ 又f(x)在x∈[2，3]上单调递减，2x在x∈[2，3]上单调递增，‎ 故f(x)-2x在x∈[2，3]上单调递减， .......（10分）‎ 当x=3时取得最小值为-10，∴m∈ ................（12分） ‎ ‎22.（1）由题意得：，当或 时，‎ 成立，∴是“局部奇函数” ......（2分）‎ （2） 由题意得：∵，‎ ‎∴在有解，∴，，‎ 令，则，‎ 设，在单调递减，在单调递增，‎ ‎∴，∴； ......（6分）‎ ‎（3）由定义得：∵，‎ ‎∴，即有解，‎ 设，∴方程等价于在时有解，‎ 设，对称轴， .........（8分）‎ ① 若，，此时，‎ ‎②若时，则此时，‎ 综上得：，即实数的取值范围是． .......（12分）‎