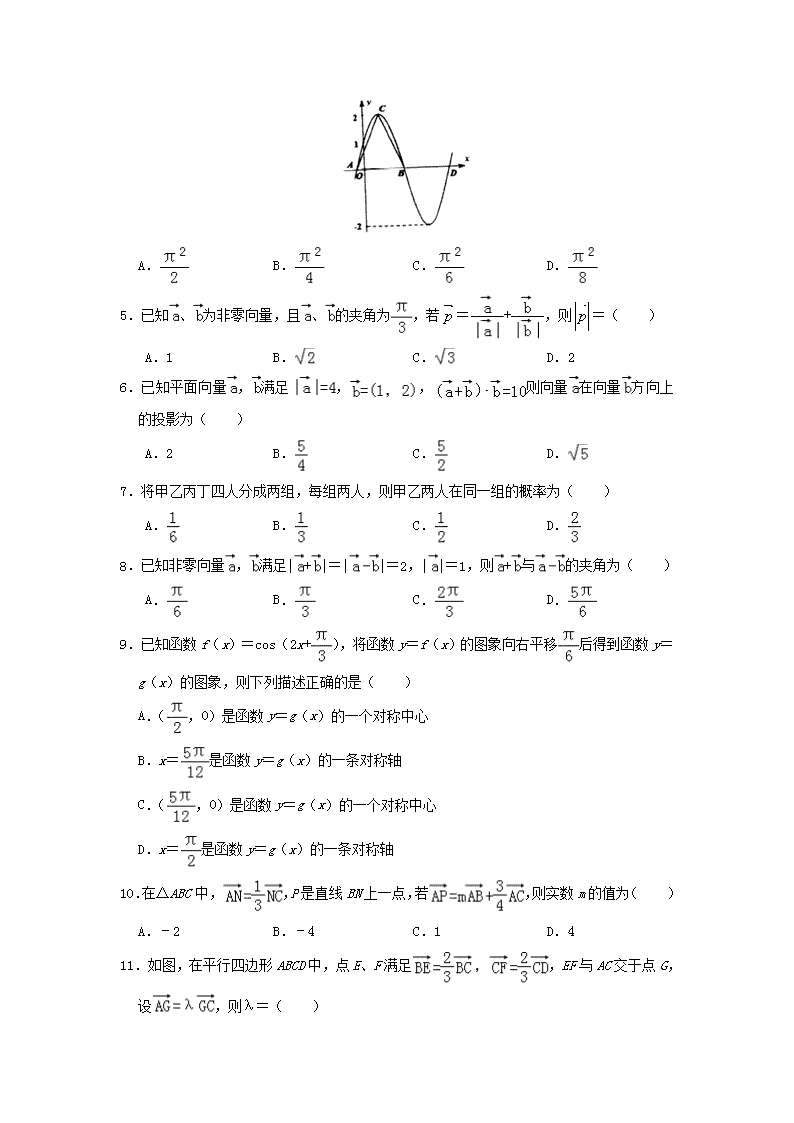2018-2019学年河南省新野县第一高级中学高一下学期第二次月考数学试题 8页

‎ ‎ ‎2018-2019学年河南省新野县第一高级中学高一下学期第二次月考数学试题 一、选择题（共12小题）‎ ‎1．已知，，，则＝（　　）‎ A． B． C． D．‎ ‎2．已知tanθ＝3，则等于（　　）‎ A． B． C．0 D．‎ ‎3．函数f（x）＝sin（ωx+φ）（x∈R）（ω＞0，|φ|＜）的部分图象如图所示，如果x1，x2∈（﹣，），且f（x1）＝f（x2），则f（x1+x2）＝（　　）‎ A． B． C． D．1‎ ‎4．已知函数y＝Asin（ωx+φ）（|φ|＜，ω＞0）图象的一部分如图所示．若A，B，D是此函数的图象与x轴三个相邻的交点，C是图象上A、B之间的最高点，点D的坐标是（，0），则数量积＝（　　）‎ A． B． C． D．‎ ‎5．已知、为非零向量，且、的夹角为，若＝+，则＝（　　）‎ A．1 B． C． D．2‎ ‎6．已知平面向量，满足，，则向量在向量方向上的投影为（　　）‎ A．2 B． C． D．‎ ‎7．将甲乙丙丁四人分成两组，每组两人，则甲乙两人在同一组的概率为（　　）‎ A． B． C． D．‎ ‎8．已知非零向量，满足|+|＝||＝2，||＝1，则+与的夹角为（　　）‎ A． B． C． D．‎ ‎9．已知函数f（x）＝cos（2x+），将函数y＝f（x）的图象向右平移后得到函数y＝g（x）的图象，则下列描述正确的是（　　）‎ A．（，0）是函数y＝g（x）的一个对称中心 ‎ B．x＝是函数y＝g（x）的一条对称轴 ‎ C．（，0）是函数y＝g（x）的一个对称中心 ‎ D．x＝是函数y＝g（x）的一条对称轴 ‎10．在△ABC中，，P是直线BN上一点，若，则实数m的值为（　　）‎ A．﹣2 B．﹣4 C．1 D．4‎ ‎11．如图，在平行四边形ABCD中，点E、F满足，EF与AC交于点G，设，则λ＝（　　）‎ A． B． C． D．‎ ‎12．已知函数f（x）＝sin（ωx+φ）（ω＞0，φ∈[，π]）的部分图象如图所示，且f（x）上[0，2π]上恰有一个最大值和一个最小值，则ω的取值范围是（　　）‎ A．[，） B．[，） C．（，] D．（，]‎ 二、填空题（共4小题）‎ ‎13．函数y＝tan（﹣x+）的递减区间是　 　．‎ ‎14．定义在（0，3）上的函数f（x）的图象如图所示＝（f（x），0），＝（cosx，0），那么不等式•＜0的解集是　 　．‎ ‎15．已知△ABC是一个面积较大的三角形，点P是△ABC所在平面内一点且++2＝，现将3000粒黄豆随机抛在△ABC内，则落在△PBC内的黄豆数大约是　 　．‎ ‎16．已知平面向量与平面向量的夹角为θ，若||＝3，，sinθ＝，则=　 　．‎ 三、解答题（共6小题）‎ ‎17．已知＝2，计算下列各式的值．‎ ‎（Ⅰ）cos2α﹣2sinαcosα﹣1；‎ ‎（Ⅱ）．‎ ‎18．（1）已知向量＝（﹣2，﹣1），＝（λ，1），若与的夹角为钝角，求λ的取值范围；‎ ‎（2）平面向量，，不共线，且两两所成的角相等，若||＝||＝2，||＝1，求：|++|．‎ ‎19．某快递公司收取快递费用的标准是：重量不超过1kg的包裹收费10元；重量超过1kg的包裹，除收费10元之外，超过1kg的部分，每超出1kg（不足1kg，按1kg计算）需要再收费5元．该公司近60天每天揽件数量的频率分布直方图如下图所示（同一组数据用该区间的中点值作代表）．‎ ‎（1）求这60天每天包裹数量的平均值和中位数；‎ ‎（2）该公司从收取的每件快递的费用中抽取5元作为前台工作人员的工资和公司利润，剩余的作为其他费用．已知公司前台有工作人员3人，每人每天工资100元，以样本估计总体，试估计该公司每天的利润有多少元？‎ ‎（3）小明打算将A（0.9kg），B（1.3kg），C（1.8kg），D（2.5kg）四件礼物随机分成两个包裹寄出，且每个包裹重量都不超过5kg，求他支付的快递费为45元的概率．‎ ‎20．已知函数f（x）＝Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π）的图象两相邻对称轴之间的距离是，若将f（x）的图象先向右平移个单位，所得函数g（x）为奇函数，函数g（x）的最大值为2．‎ ‎（1）求f（x）的解析式；‎ ‎（2）若，求f（x）的值域．‎ ‎21．已知向量＝（2，﹣1），＝（3，2），＝（m，2m+1），若点A，B，C能构成三角形，‎ ‎（1）求实数m满足的条件；‎ ‎（2）若△ABC为直角三角形，求m的值．‎ ‎22．已知函数f（x）＝sin（ωx﹣）（ω＞0）在（0，）单调增，在（，2π）单调减，‎ ‎（1）求ω的值 ‎（2）求函数y＝f（x）的单调增区间；‎ ‎（3）若方程f（x）＝m在区间[0，2π]上有两个不同的实数解x1，x2，求x1+x2的值．‎ ‎2018-2019学年高一年级下期第二次月考 数 学 答 案 一、选择题 ‎1-5 DBADC 6-10 DBCDA 11-12 CB 二、填空题 ‎13（kπ﹣，kπ+ ），k∈Z． 14．（0，1）∪（，3）‎ ‎15．1500粒 16．或．‎ 三、解答题（共6小题）‎ ‎17．解：（Ⅰ）∵＝2，可得：sinα＝3cosα，‎ ‎∴sin2α+cos2α＝（3cosα）2+cos2α＝1，解得：cos2α＝，‎ ‎∴cos2α﹣2sinαcosα﹣1＝cos2α﹣6cos2α﹣1＝﹣5cos2α﹣1＝（﹣5）×﹣1＝﹣．‎ ‎（Ⅱ）∵cos2α＝，可得：tan2α＝﹣1＝9，可得：tanα＝3，‎ ‎∴＝‎ ‎＝﹣tanα＝﹣3．‎ ‎18．解：（1）∵与的夹角为钝角；∴，且与不共线；‎ ‎∴；解得，且λ≠2；∴λ的取值范围为；‎ ‎（2）∵，，不共线，且两两所成的角相等；∴，，两两所成的角为；‎ 又；∴＝4+4+1﹣4﹣2﹣2＝1；∴．‎ ‎19．解：（1）每天包裹数量的平均数为0.1×50+0.1×150+0.5×250+0.2×350+0.1×450＝260；设中位数为x，易知x∈（200，300），则0.001×100×2+0.005×（x﹣200）＝0.5，解得x＝260．所以公司每天包裹的平均数和中位数都为260件 ‎（2）由（1）可知平均每天的揽件数为260，利润为260×5﹣3×100＝1000（元），‎ 所以该公司平均每天的利润有1000元．‎ ‎（3）设四件礼物分为二个包裹E、F，因为礼物A、C、D共重0.9+1.8+2.5＝5.2（千克），‎ 礼物B、C、D共重1.3+1.8+2.5＝5.6（千克），都超过5千克，故E和F的重量数分别有1.8和4.7，2.5和4.0，2.2和4.3，2.7和3.8，3.1和3.4共5种，‎ 对应的快递费分别为45、45、50，45，50（单位：元）故所求概率为．‎ ‎20．解：（1）∵＝2×，∴ω＝2，∴f（x）＝Asin（2x+φ）．又g（x）＝Asin[2（x﹣）+φ]为奇函数，且0＜φ＜π，则φ＝，A＝2，故f（x）＝2sin（2x+）‎ ‎（2）∵，∴2x+∈[，π]，∴sin（2x+）∈[0，1]，∴f（x）＝2sin（2x+）∈[0，2]，可得若，f（x）的值域为：[0，2]‎ ‎21．解：（1）因为＝（1，3），＝（m﹣2，2m+2），‎ 又A，B，C能构成三角形，故点A，B，C不共线，即不共线，‎ 所以3（m﹣2）﹣（2m+2）≠0，解得m≠8；‎ ‎（2）由题知△ABC为直角三角形，即有，或者或者，‎ 且＝（m﹣3，2m﹣1）所以m﹣2+3（2m+2）＝0或者m﹣3+3（2m﹣1）＝0或者（m﹣2）（m﹣3）+（2m+2）（2m﹣1）＝0，解得，m＝或者m＝或者∅，‎ 所以当△ABC为直角三角形，m的值为或m＝．‎ ‎22．解：（1）由题知sin（ω•﹣）＝1，所以，ω•﹣＝2kπ+，k∈Z，‎ 所以ω＝+，k∈Z．∵T＝≥2π，∴0＜ω＜1，∴ω＝．‎ ‎（2）由（1）知f（x）＝sin（﹣），令 2kπ+≤﹣＜2kπ+π，解得 4kπ+≤x＜4kπ+，所以函数的单调增区间是[4kπ+，4kπ+ ）．‎ ‎（3）若方程f（x）＝m在区间[0，2π]上有两个不同的实数解x1，x2，‎ 结合三角函数图象可知，y＝m 与y＝f（x）在[0，2π]上有两个不同交点．‎ ‎∵在区间[0，2π]上，﹣∈[﹣，]，∴﹣+﹣＝2×，‎ 由三角函数图象的对称性可知：x1+x2＝．‎