1. 您所在位置：首页 > 中小学教育 > 高中教育 > 教案 > 高中数学必修1教案：第二章（第15课时）指数函数2

高中数学必修1教案：第二章（第15课时）指数函数2 4页

  • 219.50 KB
  • 2021-07-01 发布

高中数学必修1教案：第二章（第15课时）指数函数2

  • 4页
  • 当前文档由用户上传发布，收益归属用户
  1. 1、本文档由用户上传，淘文库整理发布，可阅读全部内容。
  2. 2、本文档内容版权归属内容提供方，所产生的收益全部归内容提供方所有。如果您对本文有版权争议，请立即联系网站客服。
  3. 3、本文档由用户上传，本站不保证质量和数量令人满意，可能有诸多瑕疵，付费之前，请仔细阅读内容确认后进行付费下载。
  4. 网站客服QQ：403074932
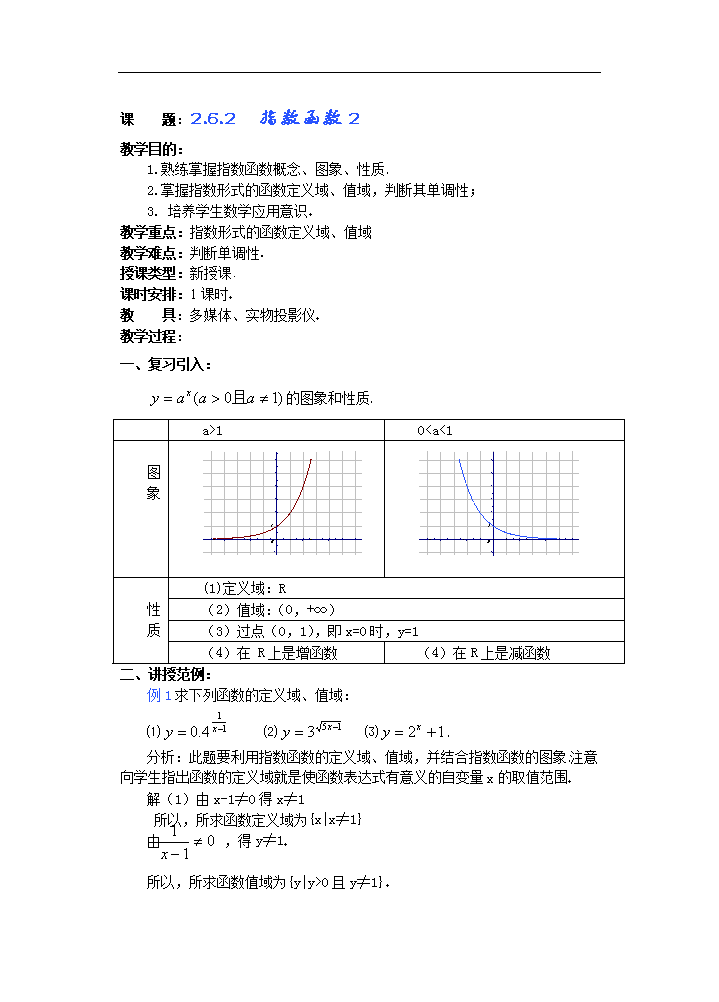
课 题：2.6.2 指数函数2‎ 教学目的： ‎ ‎1.熟练掌握指数函数概念、图象、性质 ‎2.掌握指数形式的函数定义域、值域，判断其单调性；‎ ‎3. 培养学生数学应用意识 教学重点：指数形式的函数定义域、值域 教学难点：判断单调性.‎ 授课类型：新授课 课时安排：1课时 教 具：多媒体、实物投影仪 教学过程：‎ 一、复习引入：‎ 的图象和性质 a>1‎ ‎00且y≠1}‎ 说明：对于值域的求解，在向学生解释时，可以令，考察指数函数y=,并结合图象直观地得到，以下两题可作类似处理 ‎（2）由5x-1≥0得 所以，所求函数定义域为{x|}‎ 由 ≥0得y≥1‎ 所以，所求函数值域为{y|y≥1}‎ ‎（3）所求函数定义域为R 由>0可得+1>1‎ 所以，所求函数值域为{y|y>1}‎ 通过此例题的训练，学会利用指数函数的定义域、值域去求解指数形式的复合函数的定义域、值域，还应注意书写步骤与格式的规范性 例2求函数的单调区间，并证明 解：设 ‎ 则 ‎ ∵ ∴‎ ‎ 当时， 这时 ‎ 即 ∴，函数单调递增 ‎ 当时， 这时 ‎ 即 ∴，函数单调递减 ‎ ∴函数y在上单调递增，在上单调递减 解法二、（用复合函数的单调性）：‎ 设： 则：‎ 对任意的，有，又∵是减函数 ‎∴ ∴在是减函数 对任意的，有，又∵是减函数 ‎∴ ∴在是增函数 引申：求函数的值域 （）‎ 小结：复合函数单调性的判断(见第8课时)‎ 例3设a是实数，‎ 试证明对于任意a,为增函数；‎ 分析：此题虽形式较为复杂，但应严格按照单调性、奇偶性的定义进行证明还应要求学生注意不同题型的解答方法 ‎（1）证明：设∈R,且 则 由于指数函数 y=在R上是增函数,且,‎ 所以即<0，‎ 又由>0得+1>0, +1>0‎ 所以<0即 因为此结论与a取值无关，所以对于a取任意实数，为增函数 评述：上述证明过程中，在对差式正负判断时，利用了指数函数的值域及单调性 三、练习：‎ 求下列函数的定义域和值域：‎ ‎⑴ ⑵‎ 解：⑴要使函数有意义，必须 , ‎ ‎ 当时 ； 当时 ‎ ‎ ∵ ∴ ∴值域为 ‎ ‎⑵要使函数有意义，必须 即 ‎ ‎ ∵ ∴‎ ‎ 又∵ ∴值域为 ‎ 五、小结 本节课学习了以下内容：‎ 指数形式的函数定义域、值域的求法，判断其单调性和奇偶性的方法 六、课后作业：‎ 七、板书设计（略）‎ 八、课后记：‎

您可能关注的文档

相关文档

最近下载