【数学】广西河池市2019-2020学年高一下学期期末教学质量检测试题（解析版） 13页

广西河池市2019-2020学年高一下学期 期末教学质量检测试题 考生注意：‎ ‎1．本试卷分选择题和非选择题两部分．满分150分，考试时间120分钟．‎ ‎2．考生作答时，请将答案答在答题卡上．选择题每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑；非选择题请用直径0.5毫米黑色墨水签字笔在答题卡上各题的答题区域内作答，超出答题区域书写的答案无效，在试题卷、草稿纸上作答无效．‎ ‎3．本卷命题范围：必修3、必修4．‎ 一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．‎ ‎1. 若45°角的终边上有一点，则（ ）‎ A. 2 B. ‎4 ‎C. D. ‎ ‎【答案】A ‎【解析】，即．‎ 故选：A.‎ ‎2. 下列给变量赋值的语句正确的是（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】A. ，赋值号的左边是常量，故错误；‎ B. ，赋值号的左边是表达式，故错误；‎ C. ，赋值号的左边是表达式，故错误；‎ D. ，赋值号的左边是变量，右边是表达式，故正确..‎ 故选：D ‎3. 设向量，，若，则实数m的值为（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】因为向量，，，‎ 所以，解得．‎ 故选：D.‎ ‎4. 已知扇形的弧长为2，面积是1，则扇形的圆心角的弧度数是（ ）‎ A. 4 B. ‎2 ‎C. D. ‎ ‎【答案】B ‎【解析】设扇形的圆心角弧度数为，半径为r，‎ 因为扇形的弧长为2，所以，‎ 又因为扇形面积是1，所以，解得．‎ 故选：B ‎5. 从装有3个黑球、3个白球的袋中任取3个球，若事件A为“所取的3个球中至少有1个黑球”，则与事件A对立的事件是（ ）‎ A. 所取的3个球中至多有一个黑球 B. 所取的3个球中恰有1个白球2个黑球 C. 所取的3个球都是白球 D. 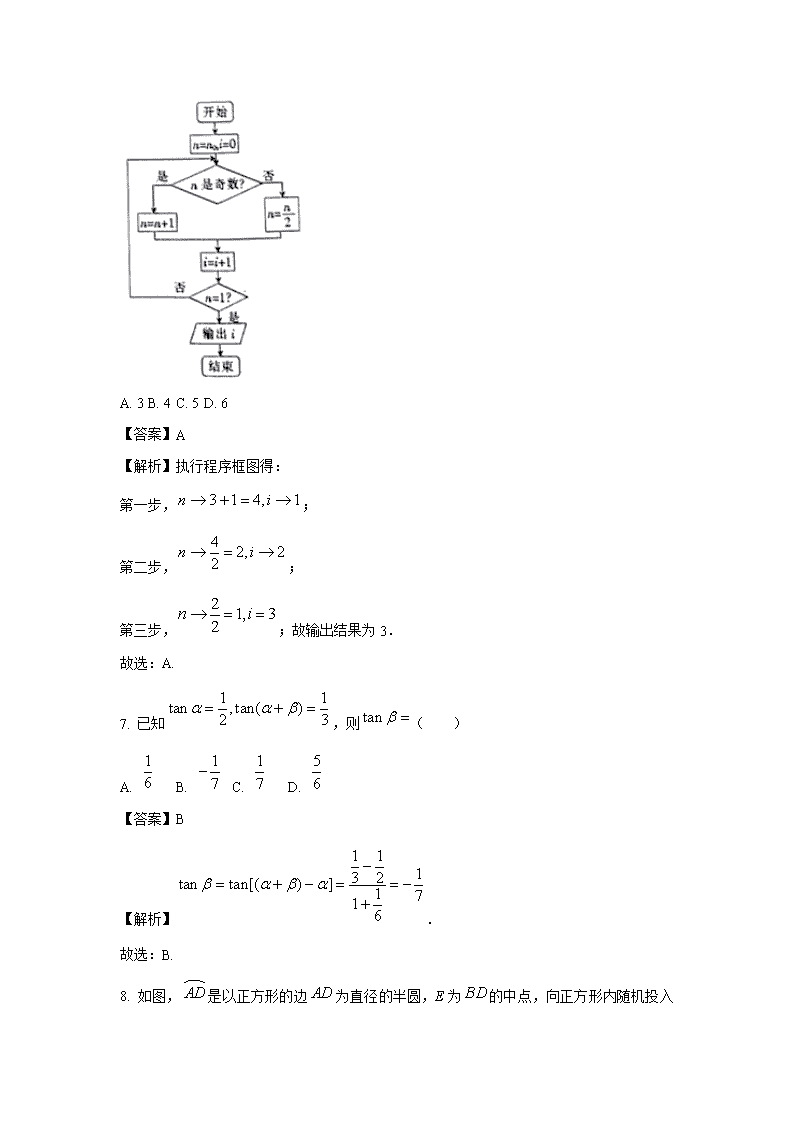所取的3个球中至少有一个白球 ‎【答案】C ‎【解析】事件{所取的3个球中至少有1个黑球}，即3黑或2黑1白或1黑2白，‎ A、B、D选项都能与事件A同时发生，所以不互斥，‎ ‎3个白球与事件A不能同时发生，是对立事件．‎ 故选：C.‎ ‎6. 执行如图所示的程序框图，若输入的，则输出的i的结果为（ ）‎ A. 3 B. ‎4 ‎C. 5 D. 6‎ ‎【答案】A ‎【解析】执行程序框图得：‎ 第一步，；‎ 第二步，；‎ 第三步，；故输出结果为3．‎ 故选：A.‎ ‎7. 已知，则（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】．‎ 故选：B.‎ ‎8. 如图，是以正方形的边为直径的半圆，E为 的中点，向正方形内随机投入一点，则该点落在阴影区域内的概率为（ ）‎ A. B. C. D. ‎ ‎【答案】D ‎【解析】设正方形的边长为2，如图所示：‎ 连结，由图形可知弓形①与弓形②面积相等，‎ 所以阴影区域的面积为：，‎ 所以该点落在阴影区域内的概率为．‎ 故选：D ‎9. 已知P是所在平面内一点，若，其中，则点P一定在（ ）‎ A. 边所在直线上 B. 边所在直线上 C. 边所在直线上 D. 的内部 ‎【答案】B ‎【解析】因为，所以，‎ 所以，所以点P在边所在直线上．‎ 故选：B ‎10. 抽样统计甲、乙两位同学的6次英语成绩，绘制成如图所示的茎叶图，则甲、乙两位同学中成绩不太稳定的同学的成绩的标准差为（ ）‎ A. B. C. 3 D. ‎ ‎【答案】A ‎【解析】，‎ ‎．‎ ‎，‎ ‎．‎ 因为，所以成绩不太稳定的是乙同学，其标准差为．‎ 故选：A．‎ ‎11. 将函数的图象向右平移个单位长度后得到函数的图象，若点是函数图象的一个对称中心，则的最小值为（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】由已知得，所以，‎ 解得，又，当时，．‎ 故选：C.‎ ‎12. 已知函数，点A，B分别为图象在y轴右侧的第一个最高点和第一个最低点，O为坐标原点，若为钝角三角形，则a的取值范围为（ ）‎ A. B. C. D. ‎ ‎【答案】B ‎【解析】由题意得，‎ 因为为钝角三角形，所以或，‎ 即，或，从而或．‎ 故选：B.‎ 二、填空题：本大题共4小题，每小题5分，共20分．‎ ‎13. 甲、乙两人进行5轮投篮训练，每轮投篮10次，每轮投进的次数如下：‎ 甲：7，7，9，7，8；‎ 乙：4，5，7，9，9．‎ 若甲的中位数为a，乙的众数为b，则__________．‎ ‎【答案】2‎ ‎【解析】由题意得，则．‎ 故答案为：2‎ ‎14. 若，且，则的值是____________．‎ ‎【答案】‎ ‎【解析】由，且，‎ 得．‎ 故答案为：.‎ ‎15. 为实现“两个一百年”的奋斗目标、实现中华民族伟大复兴的中国梦奠定坚实基础，某高校积极响应国家号召，不断加大拔尖人才的培养力度，据不完全统计：‎ 年份 ‎2016‎ ‎2017‎ ‎2018‎ ‎2019‎ 教师发表在省级刊物以上的文章篇数x ‎32‎ ‎30‎ ‎34‎ ‎36‎ 获得省级以上单位（或组织）颁奖的教师数y ‎52‎ ‎48‎ ‎57‎ ‎59‎ 根据上表可得回归方程中的为1.9，此校2020年教师发表在省级刊物以上的文章篇数为40篇，据此模型预报该校今年获得省级以上单位（或组织）颁奖的教师数为__________（结果四舍五入，精确到个位）‎ ‎【答案】67‎ ‎【解析】计算出，代入回归方程中，得，‎ 所以当时，．‎ 故答案为：67.‎ ‎16. 已知函数，对于任意的，方程 仅有一个实数根，则m的最大值为__________．‎ ‎【答案】‎ ‎【解析】利用辅助角公式，化简可得，‎ 方程仅有一个实数根，等价于函数与函数的图象的交点个数为1，结合图象可知，‎ 当时，m的最大值为．‎ 故答案为：.‎ 三、解答题：本大题共6小题，共70分．解答应写出必要的文字说明、证明过程及演算步骤．‎ ‎17. 已知．‎ ‎（1）求的值；‎ ‎（2）求的值．‎ ‎【解】（1）因为，所以，‎ 所以， ‎ ‎． ‎ ‎（2）．‎ ‎18. 已知向量，向量的夹角的正切值为，．‎ ‎（1）求向量的模；‎ ‎（2）若，求实数k的值．‎ ‎【解】（1）设向量与的夹角为，由题意有， ‎ 所以，所以，‎ 所以， ‎ ‎（2）若，得 ‎， ‎ 解得，故实数k的值为7．‎ ‎19. 从某歌唱比赛中抽取若干名选手的参赛成绩，绘制成如下的频率分布直方图．‎ ‎（1）求这些选手的平均成绩（同一组中数据用该组区间中点作代表）；‎ ‎（2）求这些选手的成绩的中位数．（精确到0.1）‎ ‎【解】解（1）由题意，得 中间值 ‎5‎ ‎7‎ ‎9‎ ‎11‎ ‎13‎ ‎15‎ 频率 ‎0.1‎ ‎0.15‎ ‎0.2‎ ‎0.3‎ ‎0.15‎ ‎0.1‎ 所以 所以这些选手的平均成绩为10.1分．‎ ‎（2）设这些选手的成绩的中位数为y，‎ 因为，‎ 所以． 所以，则，‎ 故这些选手的成绩的中位数为10.3.‎ ‎20. 已知函数的部分图象如图所示．‎ ‎（1）求函数的解析式；‎ ‎（2）求函数在区间上的值域．‎ ‎【解】解1）由图可知， ‎ 因为，所以， 所以．‎ 因为点在的图象上，‎ 所以，即，‎ 因为，所以．故． ‎ ‎（2）因为时，所以，‎ 可得，所以，‎ 所以函数在区间上的值域为.‎ ‎21. 一转眼2020年已经过半，趁着端午小长假，大家都纷纷外出走亲访友，甚至是举杯畅饮，放松一下身心，但是喝酒后千万别驾车上路行驶．为进一步消除道路交通安全隐患，确保节日期间广大市民出行平安，端午节假期前后，某市公安局交管支队第二大队连续开展了 ‎5次酒驾醉驾统一行动．交警小王在某路口连续5天对行驶的汽车每隔10辆汽车，就对司机进行酒驾呼气检测一次，确认酒驾检测结果如图所示：‎ ‎（1）问交警小王对驾驶人员的酒驾检测抽查采用的是什么抽样方法？‎ ‎（2）用分层抽样的方法对确认酒驾的驾驶人员进行抽样，若男性司机有4名，则女性司机的应抽取几名？‎ ‎（3）在（2）的条件下，在上述抽出酒驾的驾驶人员中任取2名，求这2名驾驶人员一名是男性，一名是女性的概率．‎ ‎【解】（1）交警小王对行驶汽车的驾驶人员的酒驾抽样检测，采用的是系统抽样方法； ‎ ‎（2）从题意可知，被查酒驾的男性司机：人， ‎ 女性司机有：人，‎ 设女性司机应抽取x名，依题意得，‎ 解得，即女性司机的应抽取2名， ‎ ‎（3）由（2）的结果，用表示被抽取的男性司机，表示被抽取的女性司机．‎ 则所有基本事件的总数为：，，，，，，‎ ‎，，，，，，，，共15个， ‎ 其中有1名男性司机，1名女性司机包括的基本事件的总数为：‎ ‎，共8个．‎ 所以，这2名驾驶人员一名是男性，一名是女性的概率为.‎ ‎22. 已知的三个内角分别为A，B，C，且．‎ ‎（1）求A；‎ ‎（2）已知函数，若函数 的定义域为R，且函数的最小值为，求实数k 的值．‎ ‎【解】（1）由题意有，可得， ‎ ‎∵∴，‎ ‎∴，∴． ‎ ‎（2）由题意得，，所以，‎ 所以角C的范围是， ‎ 由（1）知，所以． ‎ 设，‎ 因为，所以，‎ 则，令．‎ ‎（ⅰ）当时，此时没有最小值，不合题意 ‎（ⅱ）当时，，有，得，‎ 由，故．‎ ‎（ⅲ）当时，，有，得，‎ 由，舍去，‎ 由上知实数k的值为.‎