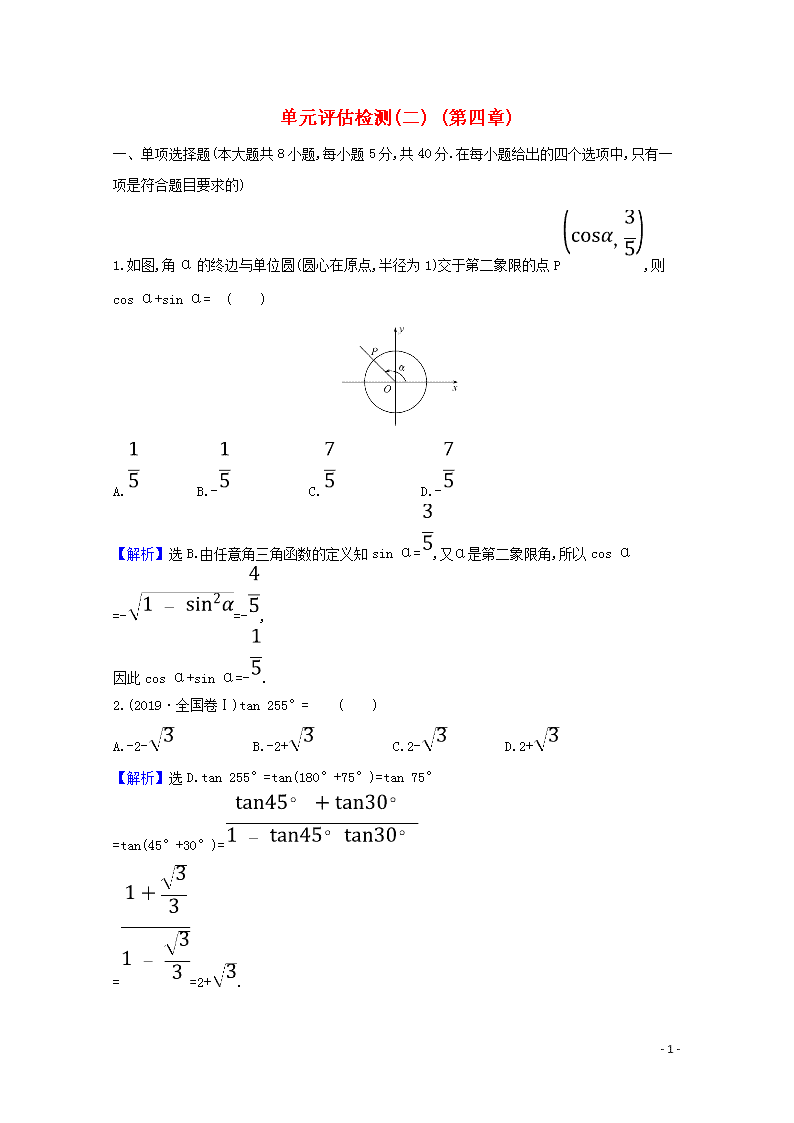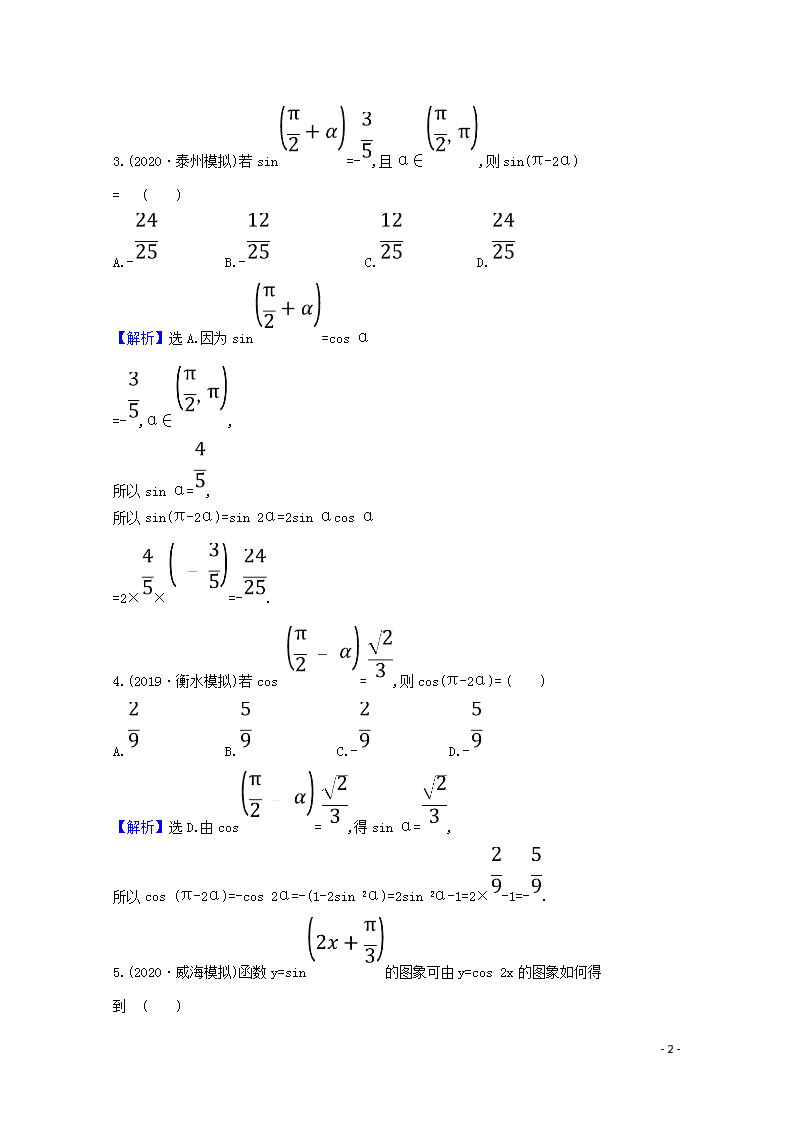2021版高考数学一轮复习单元评估检测二苏教版 16页

单元评估检测(二) (第四章)‎ 一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)‎ ‎1.如图,角α的终边与单位圆(圆心在原点,半径为1)交于第二象限的点P,则cos α+sin α= (　　)‎ A. B.- C. D.-‎ ‎【解析】选B.由任意角三角函数的定义知sin α=,又α是第二象限角,所以cos α ‎ ‎=-=-,‎ 因此cos α+sin α=-.‎ ‎2.(2019·全国卷Ⅰ)tan 255°= (　　)‎ A.-2- B.-2+ C.2- D.2+‎ ‎【解析】选D.tan 255°=tan(180°+75°)=tan 75°‎ ‎=tan(45°+30°)=‎ ‎==2+.‎ - 16 -‎ ‎3.(2020·泰州模拟)若sin=-,且α∈,则sin(π-2α)‎ ‎= (　　)‎ A.- B.-　 C. D.‎ ‎【解析】选A.因为sin=cos α ‎=-,α∈,‎ 所以sin α=,‎ 所以sin(π-2α)=sin 2α=2sin αcos α ‎=2××=-.‎ ‎4.(2019·衡水模拟)若cos =,则cos(π-2α)= (　　)‎ A.　 B. C.- D.-‎ ‎【解析】选D.由cos=,得sin α=,‎ 所以cos (π-2α)=-cos 2α=-(1-2sin 2α)=2sin 2α-1=2×-1=-.‎ ‎5.(2020·威海模拟)函数y=sin的图象可由y=cos 2x的图象如何得 到 (　　)‎ - 16 -‎ A.向左平移个单位 B.向右平移个单位 C.向左平移个单位 D.向右平移个单位 ‎【解析】选B.y=sin ‎=cos ‎=cos=cos,‎ 所以把y=cos 2x的图象向右平移个单位,得到y=cos的图象.‎ ‎6.(2020·烟台模拟)设锐角三角形ABC的内角A,B,C所对的边分别为a,b,c,若a=2,B=‎2A,则b的取值范围为 (　　)‎ A.(0,4) B.(2,2)‎ C.(2,2) D.(2,4)‎ ‎【解析】选C.因为a=2,B=‎2A,所以0<‎2A<,A+B=‎3A,所以<‎3A<π,所以0,则△ABC一定是锐角三角形 ‎【解析】选AC.由==,利用正弦定理可得==,即 tan A=tan B=tan C,A=B=C,△ABC是等边三角形,A正确;‎ 由正弦定理可得sin Acos A=sin Bcos B⇒sin ‎2A=sin 2B,‎2A=2B或‎2A+2B=π,△ABC是等腰或直角三角形,B不正确;由正弦定理可得sin Bcos C+sin Ccos B=sin B,即sin =sin B,sin A=sin B,则A=B,△ABC是等腰三角形,C正确;‎ - 16 -‎ 由余弦定理可得cos C=>0,角C为锐角,角A,B不一定是锐角,D不正确,故选AC.‎ ‎11.已知向量m=(sin x,-),n=,函数f=m·n+,下列说法正确的是 (　　)‎ A.y=f的最小正周期为π B.y=f的图象关于点对称 C.y=f的图象关于直线x=对称 D.y=f的单调增区间为(k∈Z)‎ ‎【解析】选AB.f=m·n+=sin xcos x-cos 2x+=sin 2x-cos 2x=‎ sin,其最小正周期为T==π,A正确;又sin =0,因此f(x)图象关于点对称,B正确;‎ ‎2x-=kπ+得x=+(k∈Z),因此x=-是f(x)图象的一条对称轴,C错误;由2kπ-≤2x-≤2kπ+,得kπ-≤x≤kπ+,即增区间为[kπ-,kπ+],k∈Z,D错误.‎ - 16 -‎ ‎12.将函数f(x)=2sin-1的图象上各点横坐标缩短到原来的(纵坐标不变)得到函数g(x)的图象,则下列说法不正确的是 (　　)‎ A.函数g(x)的图象关于点对称 B.函数g(x)的周期是 C.函数g(x)在上单调递增 D.函数g(x)在上最大值是1‎ ‎【解析】选ABD.将函数f(x)=2sin-1的图象上各点横坐标缩短到原来的(纵坐标不变),得到函数g(x)=2sin-1的图象,由于当x=-时,g(x)=-1,故函数g(x)的图象不关于点对称,故A错误;函数g(x)的周期为=π,故B错误;在上,2x+∈,g(x)单调递增,故C正确;在上,2x+∈,g(x)的最大值趋向于1,故D错误.‎ 三、填空题(本大题共4小题,每小题5分,共20分.请把正确答案填在题中横线上)‎ ‎13.(2019·淮安模拟)函数f(x)=sin2x+的图象在区间上的对称轴方程为________. ‎ - 16 -‎ ‎【解析】因为函数f(x)= sin,‎ 所以令2x+=+kπ,k∈Z,‎ 即x=+,k∈Z,‎ 所以当k=0时,函数f(x)= sin的图象在区间上的对称轴方程为x=.‎ 答案:x=‎ ‎14.如图,某人在山脚P处测得甲山山顶A的仰角为30°,乙山山顶B的仰角为45°,∠APB的大小为45°,山脚P到山顶A的直线距离为‎2 km,在A处测得山顶B的仰角为30°,则乙山的高度为________ km. ‎ ‎【解析】假设甲山底部为C,乙山底部为D,过A作AE⊥BD于点E.‎ 由题意可知∠APC=30°,∠BPD=45°,‎ AP=‎2 km,‎ 所以AC=AP·sin 30°=1(km),‎ DE=AC=‎1 km,设BD=h km,‎ - 16 -‎ 则DP=BD=h km,BE=(h-1)km,‎ 所以BP=h km.‎ 因为∠BAE=30°,‎ 所以AB=2BE=(2h-2)km.‎ 在△ABP中,由余弦定理得:‎ cos 45°===.解得h=2.所以乙山的高度为‎2 km.‎ 答案:2‎ ‎15.已知△ABC中,A=,cos B=,AC=8.则△ABC的面积为________;AB边上的中线CD的长为________. ‎ ‎【解析】因为cos B=,且B∈(0,π),‎ 所以sin B==.‎ 所以sin C=sin (π-A-B)=sin (A+B)=sin Acos B+cos Asin B=×+×=,‎ 在△ABC中,由正弦定理得=,‎ 即=,解得AB=7,所以△ABC的面积为S=AB·AC·sin A=×7×8×=28.‎ 在△ACD中,AD=, 所以由余弦定理得 CD2=82+-2×8××=,‎ - 16 -‎ 所以CD=.‎ 答案:28　‎ ‎16.(2020·潮州模拟)在△ABC中,角A,B,C的对边分别为a,b,c,BC边上的高为,则+的最大值是________.  ‎ ‎【解析】因为BC边上的高为,‎ 所以××a=bcsin A,‎ 即a2=2bcsin A,+=‎ ‎=‎ ‎=‎ ‎=sin A+cos A=sin≤,故+的最大值是.‎ 答案:‎ 四、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)‎ ‎17.(10分)在①B=A+,②cos C=这两个条件中任选一个,补充到下面的问题中,求 ‎(1)a的值;(2)cos ‎2C的值.‎ 在△ABC中,内角A,B,C的对边分别为a,b,c,已知b=3,cos A=,________. ‎ - 16 -‎ ‎【解析】选①.(1)因为cos A=,所以sin A===,‎ 因为B=A+,所以sin B=sin=‎ cos A=.‎ 由正弦定理得a===3.‎ ‎(2)因为B=A+,所以cos B=-sin A=-.‎ 所以sin C=sin=sin Acos B+‎ cos Asin B=×+×=,‎ 所以cos ‎2C=1-2sin ‎2C=1-=.‎ 选②.(1)因为cos A=,所以sin A==,因为cos C=,‎ 所以sin C==,‎ 所以sin B=sin[π-(A+C)]=sin(A+C)=‎ sin Acos C+cos Asin C=×+×=.‎ - 16 -‎ 由正弦定理得a===3.‎ ‎(2)cos ‎2C=2cos‎2C-1=2×-1=.‎ ‎18.(12分)(2020·天津模拟)在△ABC中,内角A,B,C所对的边分别为a,b,c.已知a>b,a=5,c=6,sin B=.‎ ‎(1)求b和sin A的值.‎ ‎(2)求sin的值.‎ ‎【解析】(1)在△ABC中,因为a>b,故由sin B=,可得cos B=.由已知及余弦定理,有b2=a2+c2-2accos B=13,所以b=.‎ 由正弦定理=,得sin A==.‎ 所以b的值为,sin A的值为.‎ ‎(2)由(1)及a