七年级下数学课件《一元一次不等式与一次函数 1 》参考课件1_鲁教版 13页

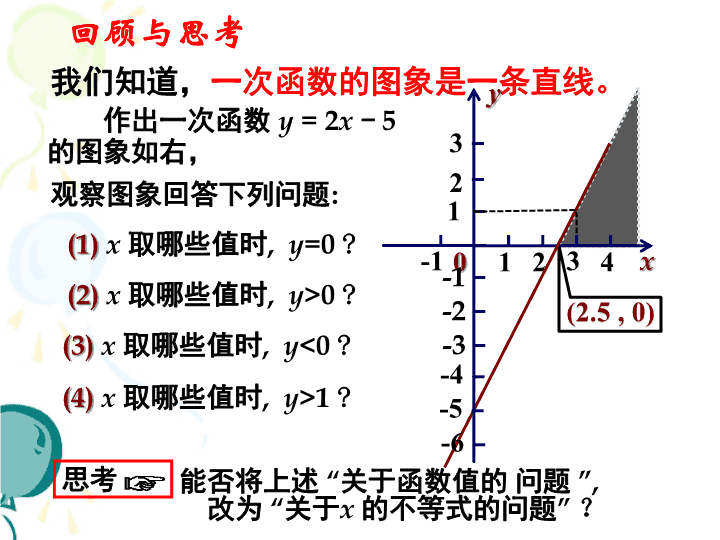
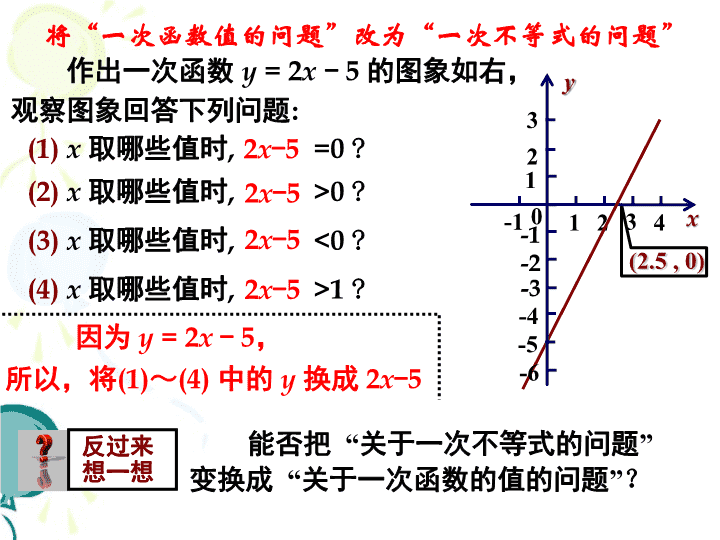
11.5 一元一次不等式 与一次函数（一） 我们知道，一次函数的图象是一条直线。 作出一次函数 y = 2x - 5 的图象如右， 观察图象回答下列问题: 思考 能否将上述 “关于函数值的 问题 ”, 改为 “关于x 的不等式的问题” ？ 1 2 3-1 4 1 -1 -2 3 -4 -3 2 -5 -6 回顾与思考 将“一次函数值的问题”改为“一次不等式的问题” 作出一次函数 y = 2x - 5 的图象如右， 观察图象回答下列问题: (1) x 取哪些值时, y =0 ? (2) x 取哪些值时, y >0 ? (3) x 取哪些值时, y <0 ? (4) x 取哪些值时, y >1 ? 0 1 2 3-1 4 1 -1 -2 3 -4 -3 2 -5 -6 因为 y = 2x – 5， 所以，将(1)～(4) 中的 y 换成 2x-5 2x-5 2x-5 2x-5 2x-5 反过来 想一想 能否把 “关于一次不等式的问题” 由上述讨易知： 函数、(方程) 不等式 “关于一次函数的值的问题” 可变换成 “关于一次不等式的问题” ； 因此， 我们既可以运用函数图象解不等式 ， 也可以运用解不等式帮助研究函数问题 ， 二者相互渗透 ，互相作用。 不等式与 函数 、方程 是紧密联系着 的一个整体 。 如果 y=-2x-5 , 那么当 x 取何值时 , y>0 ? 你解答此道题, 可有几种方法 ? 将函数问题转化为不等式问题. 即 解不等式 -2x- 5 > 0 ; 法二: 图象法。 x y -1-2-3-4-5 1-1 -2 -3 -4 -5 -6 1 2 3 由图易知， 当 x < -2.5时 y>0 . 用“函数图象法”及“解不等式法” 解函数问题 法一: 做一做 函数y1=2x-5和y2=x-2的图象如图所示，观察图象 回答下列问题： 0 1 2 3-1 4 1 -1 -2 3 -4 -3 2 -5 -6 y1=2x-5 y2=x-2 y1=y2时，两个一次函数的图象 交于一点，此点的横坐标就是 方程2x-5=x-2的解； 0 1 2 3-1 4 1 -1 -2 3 -4 -3 2 -5 -6 y1=2x-5 y2=x-2 一次函数y1=2x-5的图象在 y2=x-2的图象下方的部分对 应点的横坐标就是不等式 2x-5x-2的解； 从图象上看， 例题解析 1、已知 y1= -x+3，y2=3x-4 ，当 x 为何值时， y1>y2 ? 你是怎样做的 ? 与同伴交流. 答案: 17 .4x 例2：作出函数y1=2x－4与y2=－2x+8的图象，并观 察图象回答下列问题： （1）x取何值时，2x－4＞0？ （2）x取何值时，－2x+8＞0? （3）x取何值时，2x－4＞0与－2x+8＞0同时成立？ （4）你能求出函数y1=2x－4，y2=－2x+8的图象与x 轴所围成的三角形的面积吗？并写出过程. 例题解析 一次函数(值)的变化对应着相应自变量的取值范围 , 这个取值范围, 既可从一次函数的图象上直观看出(近 似值), 也可通过解(方程)不等式而得到(精确值). “一次函数问题”可转换成 “一次不等式的问题” ；反过来， “一次不等式的问题”可转换成 “一次函数的问题”。 我们既可以运用函数图象解不等式 ，也可以运用 解不等式帮助研究函数问题 ，二者相互渗透 ，互相作 用。不等式与 函数 、方程 是紧密联系着的一个整体 。 对于行程问题 , 应首先建立起“路程关于时间的函 数关系式”，再通过解不等式得到问题的解;或先通过 解方程求出追及(相遇)的时刻, 再解答相应的问题. 感悟与反思 （1）你掌握了哪些新的知识？ （2）你体验了哪些新的方法？ （3）你认为你本节课的表现如何？ （4）你认为本节课同学们的表现如何？ （5）通过本节课的学习，你还有哪　　　　　　　　　　　 些新的启示？ 通过本节课的学习，你有哪些收获？ P148 习题11.6 　杨扬和查程有存款分别为500元和1800元，从本月开 始，杨扬每月存400元，查程每月存200元.如果设两人存 款时间为x(月).杨扬的存款额是y1元，查程的存款额是y2 元. (1)试写出y1与x及y2与x之间的函数关系式； (2)到第几个月时，杨扬的存款额能超过查程的存款额？ 作业布置