一元一次方程及其解法第二课时教案 4页

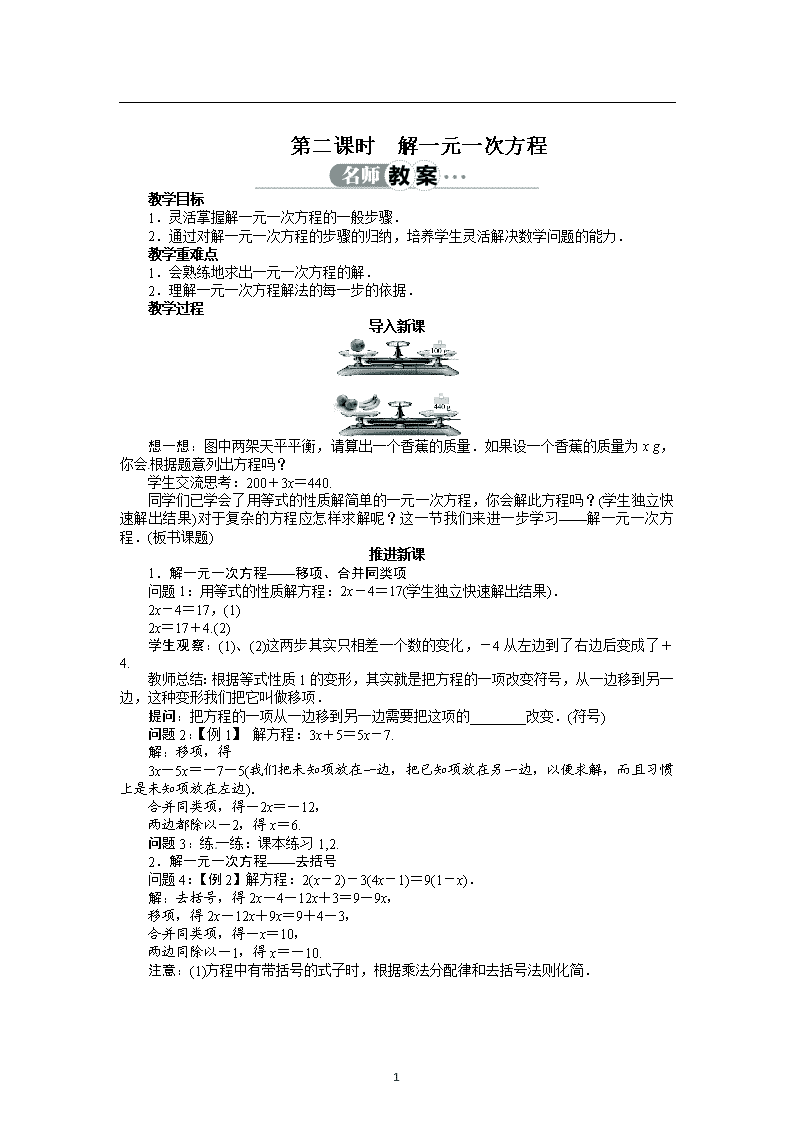
‎ ‎ 第二课时　解一元一次方程 教学目标 ‎1．灵活掌握解一元一次方程的一般步骤．‎ ‎2．通过对解一元一次方程的步骤的归纳，培养学生灵活解决数学问题的能力．‎ 教学重难点 ‎1．会熟练地求出一元一次方程的解．‎ ‎2．理解一元一次方程解法的每一步的依据．‎ 教学过程 导入新课 想一想：图中两架天平平衡，请算出一个香蕉的质量．如果设一个香蕉的质量为x g，你会根据题意列出方程吗？‎ 学生交流思考：200＋3x＝440.‎ 同学们已学会了用等式的性质解简单的一元一次方程，你会解此方程吗？(学生独立快速解出结果)对于复杂的方程应怎样求解呢？这一节我们来进一步学习——解一元一次方程．(板书课题)‎ 推进新课 ‎1．解一元一次方程——移项、合并同类项 问题1：用等式的性质解方程：2x－4＝17(学生独立快速解出结果)．‎ ‎2x－4＝17，(1)‎ ‎2x＝17＋4.(2)‎ 学生观察：(1)、(2)这两步其实只相差一个数的变化，－4从左边到了右边后变成了＋4.‎ 教师总结：根据等式性质1的变形，其实就是把方程的一项改变符号，从一边移到另一边，这种变形我们把它叫做移项．‎ 提问：把方程的一项从一边移到另一边需要把这项的________改变．(符号)‎ 问题2：【例1】 解方程：3x＋5＝5x－7.‎ 解：移项，得 ‎3x－5x＝－7－5(我们把未知项放在一边，把已知项放在另一边，以便求解，而且习惯上是未知项放在左边)．‎ 合并同类项，得－2x＝－12，‎ 两边都除以－2，得x＝6.‎ 问题3：练一练：课本练习1,2.‎ ‎2．解一元一次方程——去括号 问题4：【例2】解方程：2(x－2)－3(4x－1)＝9(1－x)．‎ 解：去括号，得2x－4－12x＋3＝9－9x，‎ 移项，得2x－12x＋9x＝9＋4－3，‎ 合并同类项，得－x＝10，‎ 两边同除以－1，得x＝－10.‎ 注意：(1)方程中有带括号的式子时，根据乘法分配律和去括号法则化简．‎ 4‎ ‎ ‎ ‎(2)去括号时不要漏乘括号内的任何一项．‎ ‎(3)若括号前面是“－”号，记住去括号后括号内各项都变号．‎ ‎(4)－x＝10不是方程的解，必须把x的系数化为1，才算完成解方程的过程．‎ 问题5：练一练：课本练习．‎ ‎3．解一元一次方程——去分母 问题6：【例3】 解方程：－2＝－.‎ 思考：(1)为使方程变为整系数方程，方程两边应该同乘以什么数？‎ ‎(2)在去分母的过程中，应该注意哪些易错的问题？‎ 解：－2＝－.‎ 去分母(方程两边同乘以各分母的最小公倍数)，得 ‎5(3x＋1)－20＝(3x－2)－2(2x＋3)，‎ 去括号，得 ‎15x＋5－20＝3x－2－4x－6，‎ 移项，得 ‎15x－3x＋4x＝－2－6－5＋20，‎ 合并同类项，得 ‎16x＝7，‎ 系数化为1，得 x＝.‎ 解上述方程的全过程，展示了一元一次方程解法的一般步骤，试归纳、小结，并了解过程中每一步的主要依据．‎ 即时小结：解方程就是要求出其中未知数的值，通过去分母、去括号、移项、合并同类项、系数化为1等步骤，就可以使一元一次方程逐步向着x＝a的形式转化，这个过程主要依据等式的性质和运算律等．‎ 问题7：巩固训练：课本练习．‎ 本课小结 ‎1．本节课你学习了什么？‎ 一元一次方程解法的一般步骤：去分母、去括号、移项、合并同类项、系数化为1.‎ ‎2．本节课应该注意什么问题？‎ ‎(1)去分母时，不要漏乘不含分母的项，分子是多项式时去掉分母要加括号；‎ ‎(2)去括号时，不要漏乘括号内的任何一项，若括号前面是“－”号，记住去括号后括号内各项都变号；‎ ‎(3)移项要变号．‎ 一、关于一元一次方程 一元一次方程的标准形式：ax＋b＝0(a≠0)，一元一次方程的最简形式：ax＝b(a≠0)，在解方程时，总是将方程化为最简形式，然后化系数为1.‎ 一般地，如果不设定a≠0，则关于x的方程ax＝b的解有如下的讨论．‎ 当a≠0时，方程有唯一解x＝；‎ 当a＝0，b＝0时，方程的解有无数个；‎ 当a＝0，b≠0时，方程无解．‎ 关于绝对值方程|x|＝a的解：当a≥0时，x＝±a；当a＜0时，无解．‎ 4‎ ‎ ‎ 二、构造一元一次方程解题七法 一元一次方程是七年级教材的重点内容之一，是学习其他方程或方程组的“基石”，构造一元一次方程可解决许多问题，其构造方法主要有以下七种：‎ ‎(一)根据一元一次方程的定义构造 ‎【例1】 当m＝________时，5x6－4m－3＝0是关于x的一元一次方程．‎ 解析：由一元一次方程的定义，可知6－4m＝1，解得m＝.‎ 答案： ‎(二)根据代数式的值相等构造 ‎【例2】 当x＝________时，代数式5x＋10与4x＋14的值相等．‎ 解析：由题意，得5x＋10＝4x＋14，‎ 解得x＝4.‎ 答案：4‎ ‎(三)根据同类项定义构造 ‎【例3】 当n为________时，3x2n－1与－xn＋2是同类项．‎ 解析：由同类项定义，得2n－1＝n＋2，‎ 解得n＝3.‎ 答案：3‎ ‎(四)根据相反数概念构造 ‎【例4】 如果2(x＋3)的值与3(1－x)的值互为相反数，那么x等于(　　)．‎ A．－8 B．8 ‎ C．－9 D．9‎ 解析：和为0的两个数互为相反数，即2(x＋3)＋3(1－x)＝0，解得x＝9，故选D．‎ 答案：D ‎(五)根据倒数概念构造 ‎【例5】 当x＝________时，代数式2x－5与互为倒数．‎ 解析：积为1的两个数互为倒数，即(2x－5)＝1，解得x＝4.‎ 答案：4‎ ‎(六)根据方程的解或同解构造 ‎【例6】 若x＝－2是方程ax－6＝15＋a的解，则a＝________.‎ 解析：将x＝－2代入原方程，得－2a－6＝15＋a，解得a＝－7.‎ 答案：－7‎ ‎【例7】 方程2x－1＝3与方程＝2的解相同，则m＝________.‎ 解析：由方程2x－1＝3，解得x＝2，因为两方程的解相同，可将x＝2代入＝2，解得m＝2.‎ 答案：2‎ ‎(七)根据非负性构造 ‎【例8】 若|2a－1|＋(b＋2)2＝0，则方程ax－b＝1的解为________．‎ 解析：因为|2a－1|，(b＋2)2都是非负数，且它们的和为0，则意味着2a－1＝0，b＋2＝0，解得a＝，b＝－2.将其代入方程，得x＋2＝1，解得x＝－2.‎ 答案：x＝－2‎ 4‎ ‎ ‎ 4‎