- 144.00 KB
- 2021-10-25 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
第九章 不等式与不等式组
9.1 不等式
教学备注
【自学指导提示】
学生在课前完成自主学习部分
9.1.2 不等式的性质
第1课时 不等式的性质
学习目标:1.熟练掌握不等式的性质1、2、3,并能灵活运用它们来解决问题,以提升自己的逻辑思维能力.
2.通过独立思考,小组合作以及自己的操作,感受不等式是刻画现实世界的有效模型.
3.激情投入,用心感受生活中无处不在的数学.
重点:不等式的性质1、2、3.
难点:不等式的性质3.[来源:Zxxk.Com]
自主学习
一、知识链接
1.什么是不等式?
2.等式有哪些性质?
二、新知预习
1.不等式的性质1:不等式两边加(或减) ,不等号的方向 .
即:如果a>b,那么a+c b+c,a-c b-c.
2.不等式的性质2:不等式的两边都乘(或除以)同一个 ,不等号的方向 .
即:如果a>b,c > 0,那么ac bc,或.
3.不等式的性质3:不等式的两边都乘(或除以)同一个 ,不等号的方向 .
即:如果a>b,c < 0,那么ac bc,或.
三、自学自测
1.用“>”或“<”填空:
(1)已知a>b,则a+3 b+3,a+x b+x;
(2)已知a>b,则a-3 b-3,a-x b-x;
(3)已知a>b,则3a 3b;
(4)已知a>b,则-3a -3b.
2.已知a>b,下列各式中,错误的是( )
A.a+6 >b+6 B.2a >2b
C.-a< -b D.5-a>5-b
四、我的疑惑
______________________________________________________________________________________________________________________________________________________
教学备注
配套PPT讲授
1.情景引入
(见幻灯片3)
2.探究点1新知讲授
(见幻灯片5-9)
3.探究点2新知讲授
(见幻灯片10-20)
课堂探究
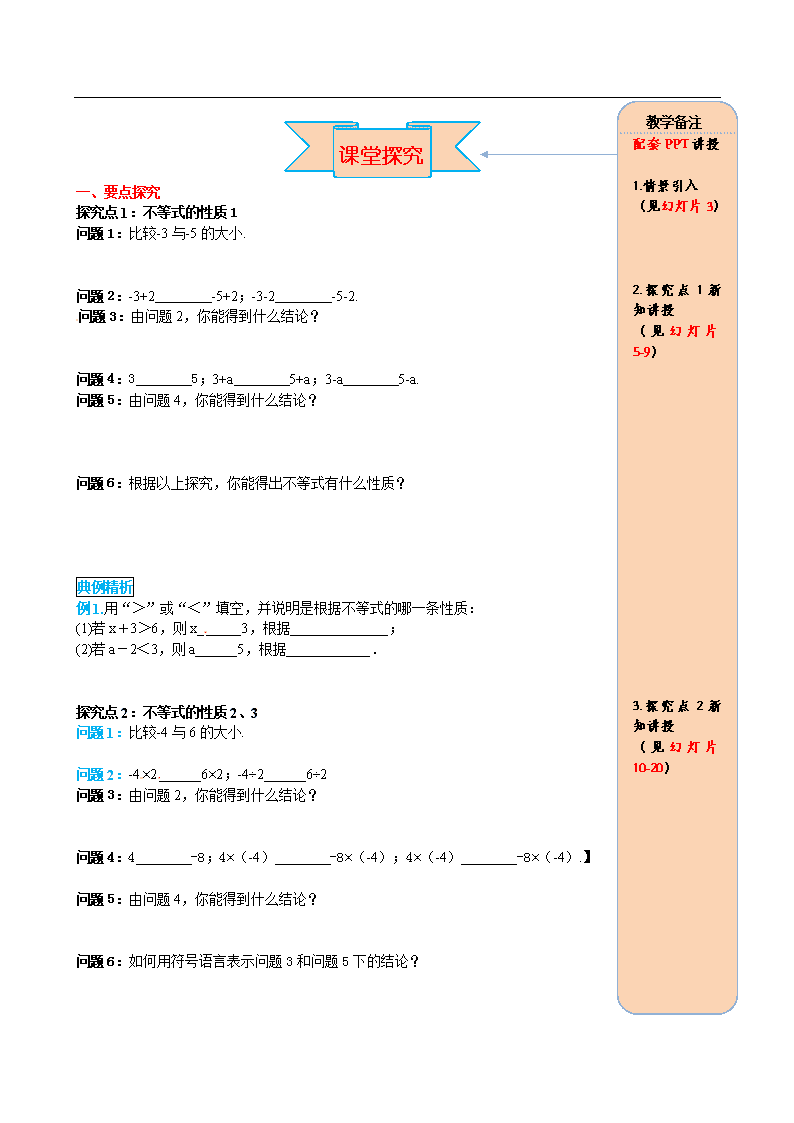
一、 要点探究
探究点1:不等式的性质1
问题1:比较-3与-5的大小.
问题2:-3+2 -5+2;-3-2 -5-2.
问题3:由问题2,你能得到什么结论?
[来源:学#科#网]
问题4:3 5;3+a 5+a;3-a 5-a.
问题5:由问题4,你能得到什么结论?
问题6:根据以上探究,你能得出不等式有什么性质?
典例精析
例1.用“>”或“<”填空,并说明是根据不等式的哪一条性质:
(1)若x+3>6,则x______3,根据______________;
(2)若a-2<3,则a______5,根据____________.
探究点2:不等式的性质2、3
问题1:比较-4与6的大小.
问题2:-4×2______6×2;-4÷2______6÷2
问题3:由问题2,你能得到什么结论?
问题4:4 -8;4×(-4) -8×(-4);4×(-4) -8×(-4).】
[来源:Z。xx。k.Com]
问题5:由问题4,你能得到什么结论?
问题6:如何用符号语言表示问题3和问题5下的结论?
典例精析
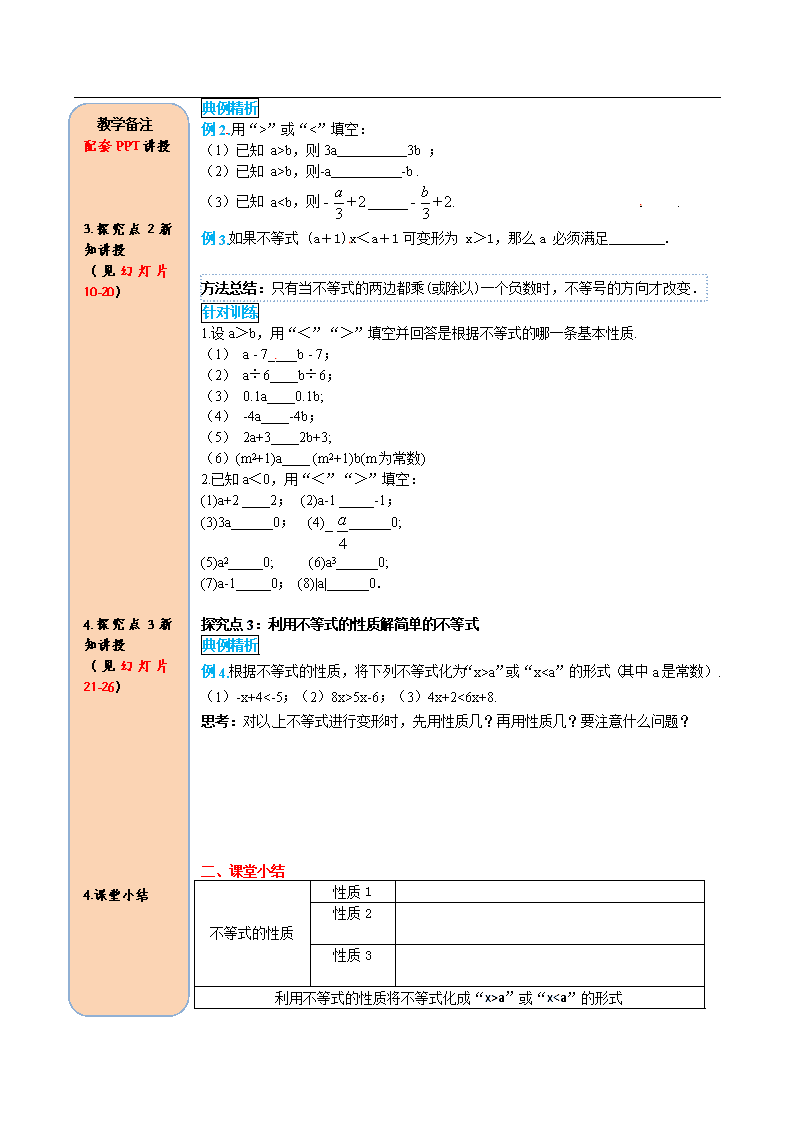
例2.用“>”或“<”填空:教学备注
配套PPT讲授
3.探究点2新知讲授
(见幻灯片10-20)
4.探究点3新知讲授
(见幻灯片21-26)
4.课堂小结
(1)已知 a>b,则3a 3b ;
(2)已知 a>b,则-a -b .
(3)已知 aa”或“x5x-6;(3)4x+2<6x+8.
思考:对以上不等式进行变形时,先用性质几?再用性质几?要注意什么问题?
二、课堂小结
[来源:Z.xx.k.Com]
不等式的性质
性质1
性质2
性质3
利用不等式的性质将不等式化成“x>a”或“x”或“<”填空:
(1)a +12 b +12 ;
(2)b-10 a -10 .
2. 把下列不等式化为x>a或x -1;
(2)-2x > 3;
(3)7x < 6x-6.
相关文档
- 不等式的性质教案(2)2021-10-223页
- 七年级下册数学同步练习9-1-2 第12021-10-222页
- 《同步导学案》人教七年级数学(下册2021-10-2212页
- 七年级下册数学教案9-1-2 第1课时 2021-10-222页
- 人教版7年级下册数学全册教案第512021-10-224页
- 2019七年级数学下册 11不等式的性2021-10-213页
- 七年级数学下册9-1-2不等式的性质2021-10-2128页
- 2019七年级数学下册 第九章 不等式2021-10-212页
- 2019七年级数学下册 第9章 不等式2021-10-212页
- 2021版高考数学一轮复习核心素养测2021-07-017页