七年级数学下册9-1-2不等式的性质课件（新版）新人教版 28页

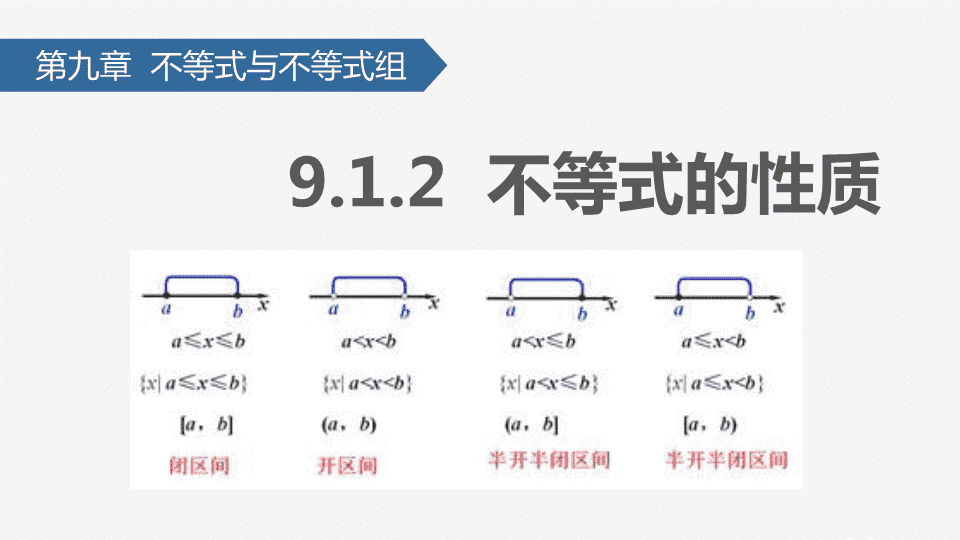
第九章 不等式与不等式组 9.1.2 不等式的性质 教学新知 性质1：不等式两边加（或减）同一个数（或式子），不等号的方向不变. 性质2：不等式两边乘（或除以）同一个正数，不等号的方向不变. 性质3：不等式两边乘（或除以）同一个负数，不等号的方向改变变. 知识要点 2.运用不等式解决有关的问题，初步认识一元一次不等式的 应用价值。 1.理解不等式的性质，会解简单的不等式，并能在数轴上表 示出解集。 知识梳理 知识点：不等式的性质 文字语言 符号语言 性质1 不等式两边加（或减）同一个 数（或式子），不等号的方向 不变. 如果a＞b，那么a+c＞b+c， a-c＞b-c. 性质2 不等式两边乘（或除以）同一 个正数，不等号的方向不变. 性质3 不等式两边乘（或除以）同一 个负数，不等号的方向改变变. 知识梳理 【例1】已知x＜y，试用“＞”或“＜”，并说明理由. (1) x+5______y+5；(2)3x______3y；(3) –3x______－3y； 【讲解】(1) 在已知不等式x＜y两边同时加上5根据不等式的性质1，在 “不等式两边都加上（或减去）同一个数（或式子），不等号的方向不 变”．故有x+5 > y+5． (2)在已知不等式x＜y两边同时乘以3根据不等 式的性质2，在“不等式两边都乘（或除以）同一个正数，不等号的方向 不变”．故有3x＜3y．(3)在已知不等式x＜y两边同时乘以－3根据不等 式的性质3，在“不等式两边都乘（或除以）同一个负数，不等号的方向 改变”．故有－3x＞－3y． ＜ ＜ ＞ 知识梳理 【方法小结】注意观察所要比较大小两个式子，是否可以看作是原来不等 式的两边作哪种变形，是加上（或减去）同一个数（或式子），或是在原 来不等式的两边同时乘（或除以）同一个数，然后依据不等式的性质确定 不等号的方向是否改变，便可比较出大小. 知识梳理 知识梳理 【方法小结】利用不等式的性质1可简化为“移项|；利用不等式的性质2或 性质3就是把未知数的系数化为1，要注意乘（或除以）同一个负数时，不 等号要改变方向. C 知识梳理 2.若x＜y，利用不等式的基本性质，填“＞”或“＜”. （1）x+2______y+2;（2）x-a______y-a;（3）1-2x______1-2y． ＜ ＞＜ 知识梳理 4.利用不等式的性质解下列不等式，并在数轴上表示解集： （1）x+3＞5；（2）-3x＞9． 答案：（1）解：根据不等式的性质1，不等式两边都减3得x+3-3＞5-3，x ＞2，这个不等式的解集在数轴上的表示为（图9-1-15）；（2）根据不等 式的性质2，不等式两边都除以-3得x＜-3，这个不等式的解集在数轴上的 表示为（图9-1-16）. 图9-1-15 图9-1-16 知识梳理 中考在线 考点：不等式的性质 【例】（2015•乐山）下列说法不一定成立的是（　　）. A．若a＞b，则a+c＞b+c B．若a+c＞b+c，则a＞b C．若a＞b，则ac2＞bc2 D．若ac2＞bc2，则a＞b 【解析】A.在不等式a＞b的两边同时加上c，不等式仍成立，即a+c＞b+c， 故本选项错误；B.在不等式a+c＞b+c的两边同时减去c，不等式仍成立， 即a＞b，故本选项错误；C.当c=0时，若a＞b，则不等式ac2＞bc2不成立， C 知识梳理 故本选项正确；D.在不等式ac2＞bc2的两边同时除以不为0的c2，该不等 式仍成立，即a＞b，故本选项错误.故选：C． 【方法小结】主要考查了不等式的基本性质．“0”是很特殊的一个数， 因此，解答不等式的问题时，应密切关注“0”存在与否，以防掉进“0” 的陷阱. 实战演练 1.（2015•怀化）下列不等式变形正确的是（　　）. A．由a＞b得ac＞bc B．由a＞b得-2a＞-2b C．由a＞b得-a＜-b D．由a＞b得a-2＜b-2 C 知识梳理 D 课堂练习 1.如果a＞b，那么不等式变形正确的是（　　）. A.a-2＜b-2 B.0.5a＜0.5b C.-2a＜-2b D.-a＞-b C ＞ ＜＞ ＞ ＜ 3.某不等式的解集如图9-1-17，则这个解集用不等式表示为 _________. x≤3 课堂练习 图9-1-17 课堂练习 课堂练习 讲评：主要考查了不等式的基本性质．“0”是很特殊的一个数，因此， 解答不等式的问题时，应密切关注“0”存在与否，以防掉进“0”的陷阱， 同时还要注意c2是个非负数. ＞ ＜ ＞ ＞ ＜＜ 课堂练习 答案：（1）＞；（2）＞；（3）＞；（4）＜；（5）＜；（6）＜. 讲评：主要考查了不等式的基本性质.（1）（2）（3）（4）直接利用不 等式的基本性质填写即可，（5）可看作这样变化而来的：a＞b，两边同 乘以-1，得-a＜-b，两边再同时加上3，得3-a＜3-b；（6）a＞b，两边 同乘以-1，得-a＜-b，两边再同时加上-18即可. 课堂练习 图9-1-18 图9-1-19 图9-1-21图9-1-20 课堂练习 7.比较3x2-2x-1与2x2-2x-5的大小. 答案：解：（3x2-2x-1）-（2x2-2x-5）=x2+4．∵x2≥0，∴x2+4＞0，∴3x2-2x-1 ＞2x2-2x-5． 讲评:本题考查了不等式的性质.这种比较两个数大小的方法称为“作差法”. 课后习题 3.若实数a，b，c在数轴上对应位置如图9-1-22所示，则下列不 等式成立的是（　　）. A.ab＞cb B.ac＞bc C.a+c＞b+c D.a+b＞c+b C D A 课后习题 图9-1-22 4.若a＞b，则下列各式中一定成立的是（　　）. ①a+2＞b+2；②ac＜bc；③-2a＞-2b；④3-a＜3-b． A．①② B．③④ C．②③ D．①④ 5.若x＜y，利用不等式的基本性质，填“＞”或“＜”： （1）x+2_____y+2；（2）x-a_____y-a；（3）1-2x_____1-2y． D ＞＜ ＜ 课后习题 答案：（1）根据不等式性质1，不等式两边都减7，不等号的方向不变， 得x+7-7＞9-7，即x＞2；（2）根据不等式性质1，不等式两边都减去5x， 不等号的方向不变，得6x-5x＜5x-5x-3，即x＜-3；（3）根据不等式性 质2，不等式两边同乘以5，不等号的方向不变，得x＜2. 7.若a＞b，且c为有理数，则ac2______bc2.≥ 课后习题 8.若不等式（2k-1）x＜2k-1的解集是x＞1,则k的范围是_______. 课后习题 11.在数轴上表示出下列不等式的解集： （1）x≥-2；（2）5x-4≤7x-1；（3）12-3x≥3（2x-3）． 课后习题 图9-1-23 图9-1-24 图9-1-25 课后习题 12. 张华在进行不等式变形时遇到不等式b＜-b，他将不等式两 边同时除以b得1＜-1，这显然是不成立，你能解释这是为什么 吗？你能求出b的取值范围吗？ 答案：解：因为不知道b的正负，所以将不等式两边同时除以b，不等号的 方向不知道改变不改变.张华把b看成大于0，所以才得出错误的结论.当b ＜0时，由1＞-1得b＜-b． 13. 某商店在举办促销活动期间，甲乙两品牌的运动鞋均打6 折．打折后，甲品牌运动鞋的价格比乙品牌运动鞋的价格低，但 课后习题