章丰富的图形世界复习材料 10页

‎ ‎ 第一章 丰富的图形世界 复习材料 ‎1 ．柱体 ‎ ‎① 正方体：它有 8 个顶点、 12 条棱、 6 个面，其中 12 条梭长都相等， 6 个面都是相等的正方形． ‎ ‎② 长方体：它有 8 个顶点、 12 条棱、 6 个面，其中各个面都是长方形（或正方形），且相对的两个面大小相等．‎ ‎ ③ 棱柱体： 〔 如图（ 1 ) ( 2 ） 〕 ，图中上下两个面称棱柱的底面，周围的面称棱柱的侧面，面与面的交线是棱柱的梭．其中侧面与侧面的交线是侧棱，棱与棱的交点是顶点．‎ 正方体和长方体是特殊的棱柱，它们都是四棱柱．正方体是特殊的长方体．‎ ‎ ④ 圆柱：图（ 3 ）中上下两个圆面是圆柱的底面，这两个底面是半径相同的圆，周围是圆柱的侧面．棱柱和圆柱统称柱体．‎ ‎ 2 ．锥体 ‎ ① 圆锥：〔 如图（ 4 ）〕 图中的圆面是圆锥的一个底面，中间曲面是圃锥的一个侧面，圆锥还有一个顶点． ‎ ‎② 棱锥：〔 如图（ 5 ）〕 图中下面多边形面是梭锥的一个底面，其余各三角形面是棱锥的侧面，各侧面的交线是棱锥的侧棱，各侧棱的交点是棱锥的顶点．棱锥和回锥统称锥体． ‎ ‎3 ．台体 ‎ ‎① 圆台： 〔 如图（ 6 ） 〕 图中上下两个不同的国面是圆台的底面，中间曲面是圆台的一个侧面．‎ ‎② 棱台： 〔 如图（ 7 ） 〕 图中上、下两个多边形是棱台的底面，其余四边形面是棱台的侧面，各侧面的交线是棱台的侧棱，底面和侧面誉。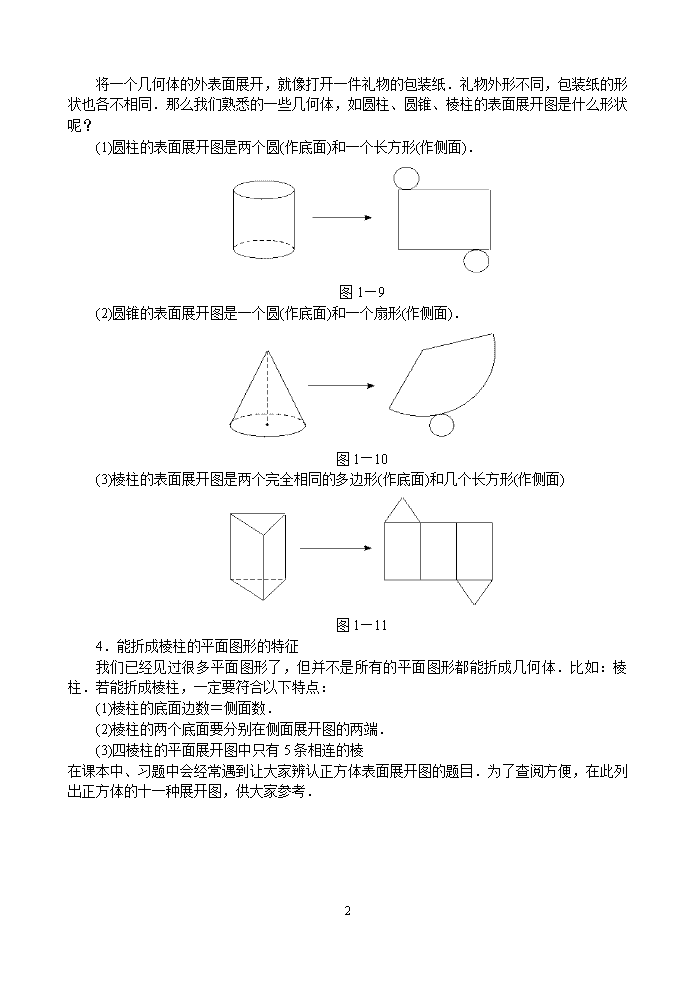的交线是棱，梭与侧棱的交点是棱台的顶点． ‎ ‎4 ．球体： 〔 如图（ 8 ） 〕 图中半圆绕其直径旋转而成的几何体，如篮球、足球等都是球体．‎ ‎ ‎ 部分几何体的平面展开图．‎ 10‎ ‎ ‎ 将一个几何体的外表面展开，就像打开一件礼物的包装纸．礼物外形不同，包装纸的形状也各不相同．那么我们熟悉的一些几何体，如圆柱、圆锥、棱柱的表面展开图是什么形状呢？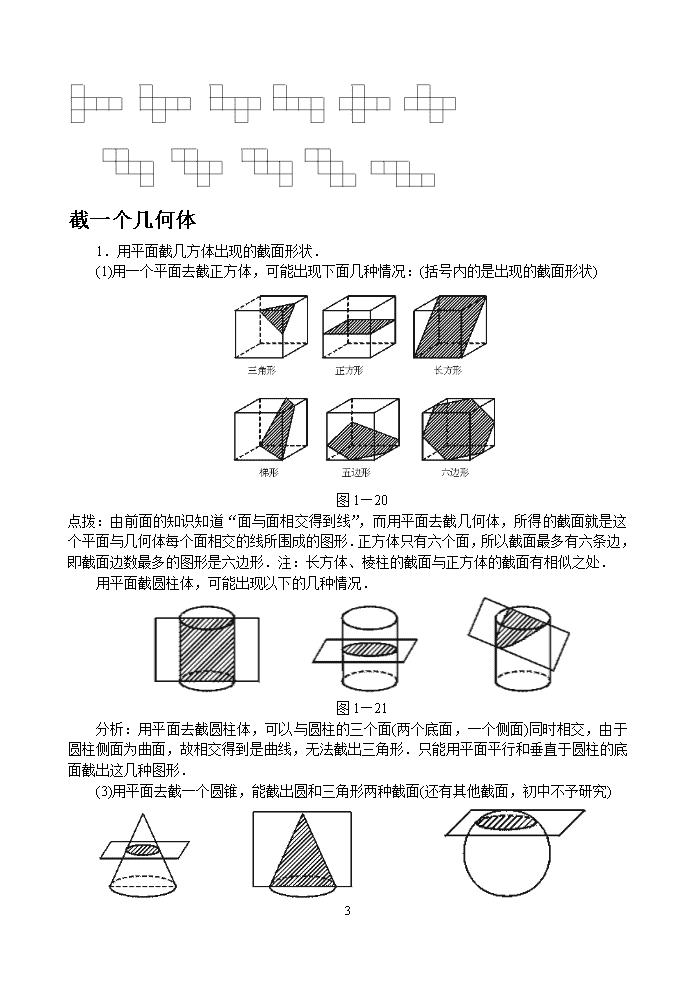‎ ‎(1)圆柱的表面展开图是两个圆(作底面)和一个长方形(作侧面)．‎ 图1—9‎ ‎(2)圆锥的表面展开图是一个圆(作底面)和一个扇形(作侧面)．‎ 图1—10‎ ‎(3)棱柱的表面展开图是两个完全相同的多边形(作底面)和几个长方形(作侧面)‎ 图1—11‎ ‎4．能折成棱柱的平面图形的特征 我们已经见过很多平面图形了，但并不是所有的平面图形都能折成几何体．比如：棱柱．若能折成棱柱，一定要符合以下特点：‎ ‎(1)棱柱的底面边数＝侧面数．‎ ‎(2)棱柱的两个底面要分别在侧面展开图的两端．‎ ‎(3)四棱柱的平面展开图中只有5条相连的棱 在课本中、习题中会经常遇到让大家辨认正方体表面展开图的题目．为了查阅方便，在此列出正方体的十一种展开图，供大家参考．‎ 10‎ ‎ ‎ 截一个几何体 ‎1．用平面截几方体出现的截面形状．‎ ‎(1)用一个平面去截正方体，可能出现下面几种情况：(括号内的是出现的截面形状)‎ 图1—20‎ 点拨：由前面的知识知道“面与面相交得到线”，而用平面去截几何体，所得的截面就是这个平面与几何体每个面相交的线所围成的图形．正方体只有六个面，所以截面最多有六条边，即截面边数最多的图形是六边形．注：长方体、棱柱的截面与正方体的截面有相似之处．‎ 用平面截圆柱体，可能出现以下的几种情况．‎ 图1—21‎ 分析：用平面去截圆柱体，可以与圆柱的三个面(两个底面，一个侧面)同时相交，由于圆柱侧面为曲面，故相交得到是曲线，无法截出三角形．只能用平面平行和垂直于圆柱的底面截出这几种图形．‎ ‎(3)用平面去截一个圆锥，能截出圆和三角形两种截面(还有其他截面，初中不予研究)‎ ‎　　　　　　‎ 10‎ ‎ ‎ 图1—22　　　　　　　　　　　　　　　　　　图1—23‎ ‎(4)用平面去截球体，只能出现一种形状的截面——圆．‎ 需要记住的要点： ‎ 几何体 截面形状 正方体 三角形、正方形、长方形、梯形、五边形、六边形 圆 柱 圆、长方形、正方形、……‎ 圆 锥 圆、三角形、……‎ 球 圆 三视图 主视图、左视图、俯视图的定义 从不同方向观察同一物体，从正面看到的图叫主视图，从左面看到的图叫左视图，从上面看到的图叫做俯视图．‎ 几种几何体的三视图 ‎(1)正方体：三视图都是正方形．‎ 图1—27‎ ‎(2)球：三视图都是圆．‎ 图1—28‎ 提醒：在所有几何体中，只有正方体与球这两种几何体的三视图是相同的．‎ ‎(3)圆柱体：‎ 图1—29‎ ‎(4)圆锥体：‎ 10‎ ‎ ‎ 图1—30‎ 圆锥的主视图、左视图都是三角形，而俯视图的图中有一个点表示圆锥的顶点，因为从上往下看圆锥时先看到圆锥的顶点，再看到底面的圆．‎ 如何画三视图 当用若干个小正方体搭成新的几何体，如何画这个新的几何体的三视图？‎ ‎(1)由照片画三视图．‎ 由照片可以清楚地看到每个小正方体的位置，这样画三视图比较直观．画三视图，都要注意从这个方向看时几何体有几列，每列有几个正方体(即有几层)，根据看到的列数、层数，画出相应的图．‎ 注意：主视图与左视图中每列的正方形都是从下往上排，底层整齐，不能出现悬空．而俯视图则有可能出现中空的现象．如右图：‎ 从正面看，2列，每列一层；从左面看，2列，每列一层；从上面看，2列，左列2层，右列一层．则三视图是：‎ 图1—31‎ 注意：照片中的几何体为了使大家看清前后情况，因此照片中的物体一般朝左偏的位置是正面．‎ ‎(2)由俯视图画主视图、左视图．‎ 解法一：根据俯视图摆出几何体，按照(1)的方法画主视图、左视图．‎ 解法二：直接由俯视图确定主视图、左视图的列数、层数，并画出图．‎ ‎①主视图与俯视图列数相同，俯视图中每列的方框内的最大数字即为主视图本列的层数．‎ ‎②左视图的列数与俯视图的行数相同，俯视图每一横行的方框内的最大数字，就是这一横行逆时针转90°所成的左视图中的列的层数．‎ 如：俯视图 10‎ ‎ ‎ 俯视图2列，则主视图也有两列，左列中的三个方框中最大的是3，右列是1，所以主视图左列三层，右列一层；俯视图三行，则左视图有三列，俯视图从上至下三行最大数字分别为1，2，3，则左视图三列从左至右分别有1，2，3层．画图如下．‎ ‎(3)其他几何体的三视图：‎ 从某方向看时，这个几何体最大边缘的形状及能够看到的顶点及棱．‎ 例题应用 例1：用平面截下列几何体，找出相应的截面形状．‎ ‎(1)‎ ‎(2)‎ ‎(3)‎ 10‎ ‎ ‎ 图1—24‎ 点拨：看图选项关键是要找出平面截几何体的方向和角度，找出：它可能与几个面相交，截面就是几边形；与平面相交得直线，与曲面相交得曲线．‎ 解答：(1)B　(2)C　(3)A 补充：1．圆台 用平面截圆台，截面形状会有圆和梯形这两种较特殊图形，截法如下：‎ 图1—25‎ ‎2．棱锥 由于棱锥同时具有棱柱的侧面是平面的特点，又具备了圆锥的锥点的特征．所以截面形状必须兼顾这两方面．截面可能出现的形状是三角形、多边形、梯形．‎ 例2：［例1］根据每组三视图，判断几何体形状：‎ ‎(1)先看什么比较明显呢？‎ 图1—33‎ ‎(2)‎ 10‎ ‎ ‎ 图1—34‎ 点拨：(1)中俯视图是六边形，说明是柱或是锥，而主视图、左视图都是矩形，说明是柱即六棱柱．(2)中由主视图、左视图是三角形说明是锥体，而底面是四边形，说明不是圆锥，而是棱锥，是四棱锥．俯视图中的点是锥点，四条线段是锥的四条棱．‎ 解答：(1)六棱柱　(2)四棱锥 达标测试 一、连一连 ‎ ‎ ‎ ‎ 棱柱 圆锥 球 正方体 长方体 圆柱 二、填一填 1． 图形是由_______、_______、_______构成的．‎ 2． 长方体有________个顶点，_______条棱，_______个面，这些面的形状都是________．‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ 3． 圆锥是由______个面围成的，它们的交线为_________．‎ 4． 从一个六边形的某个顶点出发，分别连接这个顶点与其余各顶点，可以把这个六边形分割成_______个三角形．‎ 5． 如图是一个正方体的展开图，请问1号面的对面是______号面．‎ 三、选一选 ‎1．关于棱柱下列说法正确的是（ ）‎ A 棱柱侧面的形状可能是一个三角形 B 棱柱的每条棱长都相等 ‎ C 棱柱的上、下底面的形状相同 D 棱柱的棱数等于侧面数的2倍 ‎ ‎2．指出图中几何体截面的形状是 （ ）‎ 10‎ ‎ ‎ ‎ ‎ ‎ A B C D ‎3．下面图形经过折叠可以围成一个正方体的是 （ ）‎ ‎ ‎ ‎ A B C D ‎ ‎4．用一个平面去截正方体，截面的形状不可能是 （ ）‎ ‎ A 三边形B 长方形 C 六边形 D 七边形 ‎ ‎5．如右上图所示，电视台的摄像机1、2、3、4在不同位置拍摄了四幅画面，则A图象是______号摄像机所拍，B图象是______号摄像机所拍，C图象是______号摄像机所拍，D图象是______号摄像机所拍。‎ 五、画一画 1． 下面是由五块积木搭成的，这几块积木都是相同的正方体．请你画出这个图形的主视图、左视图、俯视图．‎ 2． 如图是由几个小正方体块积木搭成的几何体俯视图，小正方形中的数字表示该位置的小正方体块的个数．请你画出这个图形的主视图、左视图．‎ ‎1‎ ‎2‎ ‎3‎ ‎1‎ 10‎ ‎ ‎ 六、想一想 有一个正方体，在它的各个面上分别涂着红、黄、蓝、绿、紫、黑六种颜色，小明、小颖和小刚三位同学从三个不同的角度去观察此正方体，观察结果如图所示，问这个正方体各个面上的颜色对面各是什么颜色？‎ 10‎