青岛初中数学七年级下册11.4 多项式乘多项式   整式的乘除 26页

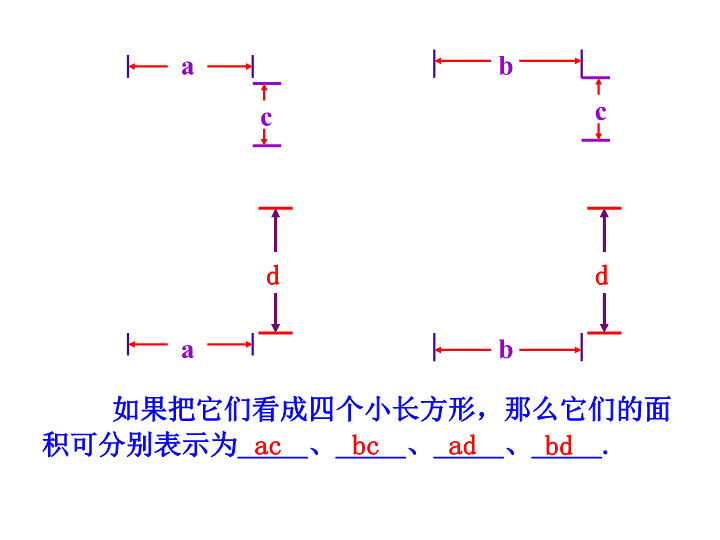
11.4 多项式乘多项式 　 整式的乘除 回忆 １.单项式乘单项式的法则 ２.单项式乘多项式的法则 如果把它们看成四个小长方形，那么它们的面积 可分别表示为_____、_____、_____、_____. d ac adbc d a b a b c c bd d a b c d a b c 如果把它看成一个大长方形，那么它的边长 为_____、_____,面积可表示为_________.c+d (a+b)(c+d)a+b d a b c 如果把它看成一个大长方形，那么它的面积可表 示为______________. 如果把它们看成四个小长方形，那么它们的面积 可分别表示为_____、_____、_____、_____.ac adbc bd ac+bc+ad+bd(a+b)(c+d) (a+b)(c+d) (a+b)(c+d) ad+ bcac+ ac+bc+ad+bd(a+b)(c+d) bd+ 这个运算过程,可以表示为 如何进行多项式乘多项式的运算? 多项式与多项式相乘，先用一个 多项式的每一项分别乘另一个多项式 的每一项，再把所得的积相加. (1) (x+2y)(5a+3b) ; (2) (2x–3)(x+4) ; 解：(x+2y)(5a+3b) = = 解：(2x–3)(x+4) 2x2 +8x –3x –12 =2x2 +5x 例1 计算: = –12 x ·5a +x ·3b +2y ·5a +2y ·3b 5ax+3bx+10ay+6by 注意:多项式与多项式相乘的结果中,要合并同类项. 计算： )7)(3( yxyx （1） )23)(52( yxyx （2） ))(( 22 yxyxyx （3） 感悟新知 计算： )7)(5(  xx（1） ( 7 )( 5 )x y x y （2） )32)(32( nmnm （3） )32)(32( baba （4） 你注意到了吗？ 多项式乘以多项式，展开 后项数很有规律，在合并同类 项之前，展开式的项数恰好等 于两个多项式的项数的积。 1.漏乘 2.符号问题 3.最后结果应化成最简形式. 2)1()2)(32(  xxx 判别下列解法是否正确， 若错请说出理由. 解：原式 )1)(1(642 2  xxxx )12(642 22  xxxx 12642 22  xxxx 522  xx 3x 2)1()2)(32(  xxx 判别下列解法是否正确， 若错请说出理由. 解：原式 )1(6342 222  xxxx 1672 22  xxx 772  xx ( 1)( 1)x x  2( 2 1)x x   2)1()2)(32(  xxx 判别下列解法是否正确， 若错请说出理由. 解：原式 )1)(1(6342 2  xxxxx 12672 22  xxxx 792  xx 2( 2 1)x x   2 2 1x x   2 5 5x x   说一说： 注 意 ! §1.计算(2a+b)2应该这样做： § (2a+b)2=(2a+b)(2a+b) § =4a2+2ab+2ab+b2 § =4a2+4ab+b2 § 切记 一般情况下 § (2a+b)2不等于 4a2+b2 . 注 意 ! § 2.(3a–2)(a–1)–(a+1)(a+2)是多项 式的积与积的差，后两个多项式 乘积的展开式要用括号括起来。 § 3. (x+y)(2x–y)(3x+2y)是三个多 项式相乘，应该选其中的两个先 相乘，把它们的积用括号括起来， 再与第三个相乘。 （1） )32)(1(  xx （2） )37)(37( xx  （3） )12)(2(  nnn 1 、计算 （4） 2)56( a 2.化简： )13)(12)(1( 2  xxx )2(2)12(3)2( 22  xxxxx 3.先化简，再求值： )2)(1(6)32)(13(  aaaa 3a其中 思考题 4、解方程 5)12)(32()5)(2(4  xxxx 5、如果a2＋a=1,那么求(a－5)(a＋6)的值 6、若(x＋m)(x－2)的积中不含关于x的 一次项，求m的值 拓展延伸 拓展延伸 7、如果(x2+bx+8)(x2 – 3x+c)的 乘积中不含x2和x3的项，求b、c的 值。 解：原式= x4 – 3x3 + c x2 +bx3 – 3bx2 +bcx+8 x2– 24x+8c X2项系数为：c –3b+8 X3项系数为：b – 3 = 0 = 0 ∴ b=3 , c=1 填空： ____)3)(2( 2  xxxx ____)3)(2( 2  xxxx ____)3)(2( 2  xxxx ____)3)(2( 2  xxxx __________))(( 2  xxbxax 观察上面四个等式，你能发现什么规律？ )( ba ab 你能根据这个规律解决下面的问题吗？ 5 6 1 (-6) (-1) (-6) (-5) 6 2( 7)( 5) __ __x x x x  － ＋ 口答： 2（－） （－35）