七年级下数学课件：5-1-1 相交线 （共16张PPT）_人教新课标 16页

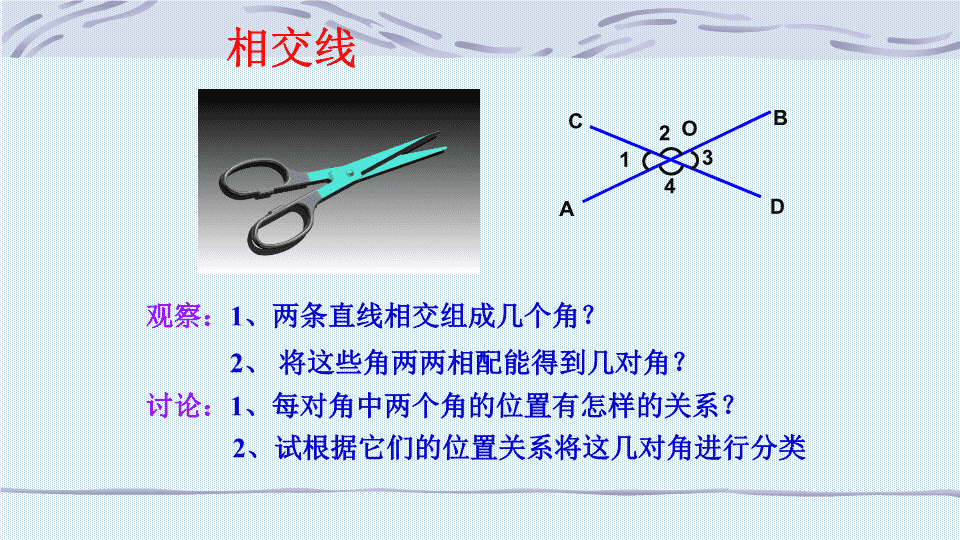
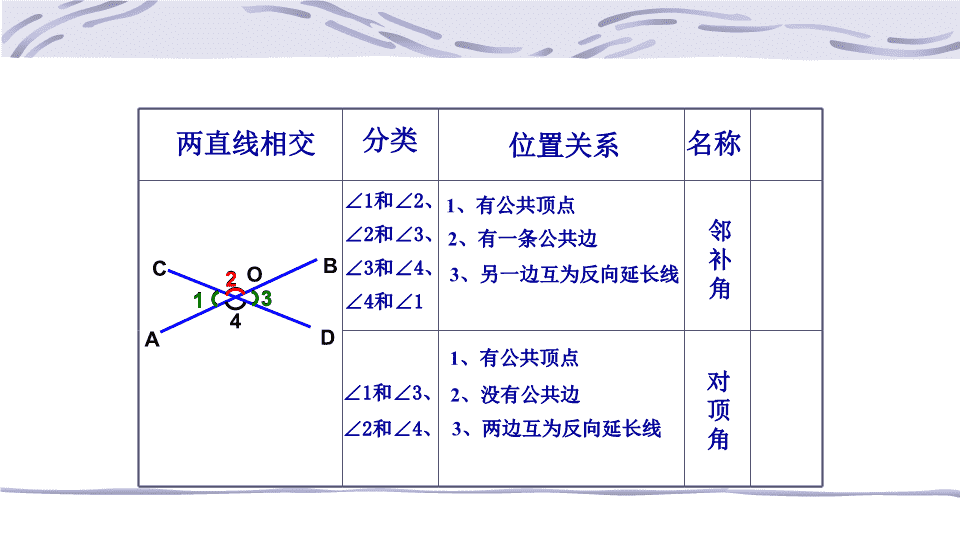
相交线 观察：1、两条直线相交组成几个角？ 讨论：1、每对角中两个角的位置有怎样的关系？ 2、 将这些角两两相配能得到几对角？ 2、试根据它们的位置关系将这几对角进行分类 B A C D O 1 2 3 4 B A C D O 1 2 3 4 1、有公共顶点 分类 ∠1和∠2、 ∠2和∠3、 ∠3和∠4、 ∠4和∠1 ∠1和∠3、 ∠2和∠4、 1、有公共顶点 位置关系 邻 补 角 对 顶 角 2、有一条公共边 3、另一边互为反向延长线 2、没有公共边 两直线相交 3、两边互为反向延长线 名称 O A BC D ）（1 3 4 2 ） （ O A BC D ）（1 3 4 2 ） （ 练习：下列图中，∠1与∠2是对顶角吗？为什么？ 否 是 否 否 （1） （2） （3） （4） 1 2 1 2 1 2 1 2 做一做：分别用量角器量一量4个交角的 度数，各类角的度数有什么关系？ B A C D O 1 2 3 4 所以∠1=∠3 同理∠2=∠4 ∠2与∠3互补 答：因为∠1与∠2互补， （邻补角定义） (同角的补角相等) 1、有公共顶点 分类 ∠1和∠2、 ∠2和∠3、 ∠3和∠4、 ∠4和∠1 ∠1和∠3、 ∠2和∠4、 1、有公共顶点 位置关系 邻 补 角 对 顶 角 邻 补 角 互 补 2、有一条公共边 3、另一边互为反向延长线 2、没有公共边 两直线相交 3、两边互为反向延长线 名称 大小 关系 对 顶 角 相 等 B A C D O 1 2 3 4 1、若∠1与∠2是对顶角，∠1=160，则∠2=______0； 若 ∠3与∠4是邻补角，则∠3+∠4 =______0 180 180 2、若∠1与∠2为对顶角，∠1与∠3互补，则 ∠2+∠3= 0 16 练习： 3、图中是对顶角量角器，你能说 出用它测量角的原理吗？ 答：对顶角相等。 例1：如图,直线a、b相交。 （1） ∠ 1=400， 求∠2，∠3，∠4的度数。 （2） ∠1:∠2=2:7 ，求各角的度数。 b a 1 2 34 ∠2＝180°－∠1 ＝180°－ 40° 解：（1）由邻补角的定义，可得 ＝140° 由对顶角相等，可得 ∠3＝∠1＝40° ∠4＝∠2＝140° 解：∵∠DOB=∠ ，（ ） =80°（已知） ∴∠DOB= 　°（等量代换） 又∵∠1=30°（ ） ∴∠2=∠ -∠ = - = ° 1、一个角的对顶角有 个，邻补角最多有 个，而补角则可以有 个。 3、如图，直线AB、CD相交于 O，∠AOC=80°∠1=30°； 求∠2的度数. A C B D E 1 一 两 无数 AOC ∠AOC DOB 1 80° 30° 50 对顶角相等 已知 二、 填空 80 2、右图中∠AOC的对顶角是 , 邻补角是 . ∠DOB ∠AOD和∠COB 2) ) O 1、如图1，三条直线ＡＢ、ＣＤ、 ＥＦ两两相交，在这个图形中，有 对顶角_____对，邻补角____ 对.6 12 ∠AOD ∠BOD ∠AOD ∠COE ∠3、 2、如图2，直线ＡＢ、ＣＤ 相交于O，ＯＥ是射线。则 ∠3的对顶角是_____________， ∠1的对顶角是_____________， ∠1的邻补角是_____________， ∠2的邻补角是_____________。 练习： C E A B F D 图1 C A E D B O1 2 3 图2 4、已知两条直线相交成的四个角，其中一个 角是900，其余各角是_____ 。 900 850 5、如图4，三条直线a，b，c相交 于点O，∠1=400，∠2=550，则 ∠3=_____. 3、如图3，∠2与∠3为邻补角， ∠1=∠2，则∠1与∠3的关系 为 。互补 A E D CB 1 3 2 图3 a b c o1 23 图4 6、如图，已知直线AB，CD相交于点O，OA平分∠EOC， ∠EOC=700，求∠BOD，∠BOC的度数。 解：因为OA平分∠EOC，∠EOC= 700 所以∠AOC=350 由对顶角相等，得 由邻补角定义，得 ∠BOC= 180°－∠AOC = 180°－ 35° = 145° ∠BOD=∠AOC=350 E A D C O B 角的名称 邻补角 对顶角 位置关系 2、有一条公共边 3、另一边互为反向延长线 4 .两条直线相交形成的角 1、有公共顶点 1、有公共顶点 2、没有公共边 3、两边互为反向延长线 4. 两条直线相交而成； 性质 邻 补 角 互 补 对 顶 角 相 等 相同点 ①都是 两条直 线相交 而成的 角； ② 都有一 个公共 顶点； ③都是 成对出 现的 不同点 1. 对 顶角 没有公共边而 邻补角有一条 公共边； 2.两条直线 相交时，一个 角的对顶角只 有一个，而一 个角的邻补角 有两个. 对顶角有两对, 邻补角有四对 知识回顾： 思考题： 两条直线相交于一点，有几对对顶角？ 三条直线相交于一点，有几对对顶角？ 四条直线相交于一点，有几对对顶角？ n 条直线相交于一点，有几对对顶角？