七年级下册数学课件《平行线及其判断》 人教新课标 (10) 13页

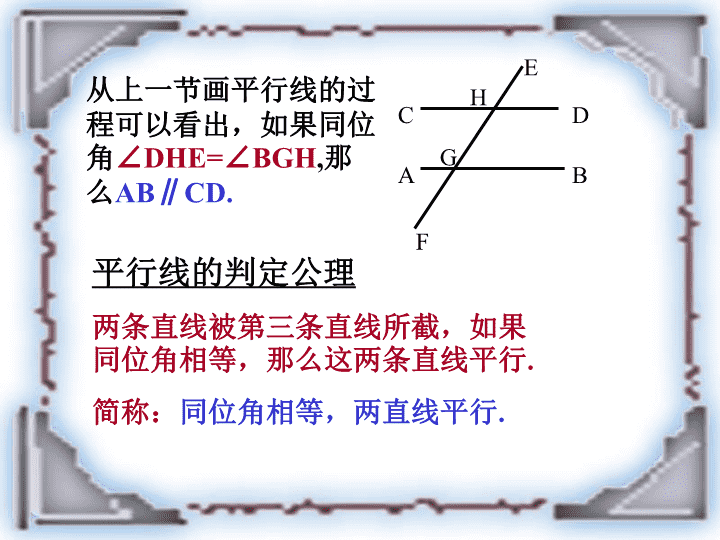
我们已会用那些知识 判断两条直线平行？ 1.平行线的定义 在同一平面内不相交的两条直线叫做平行线 从上一节画平行线的过 程可以看出，如果同位 角∠DHE=∠BGH,那 么AB∥CD. C E DH A F G B 平行线的判定公理 两条直线被第三条直线所截，如果 同位角相等，那么这两条直线平行. 简称：同位角相等，两直线平行. 例1 已知直线AB与CD被直线EF所截，且∠1=∠2. 试证明 AB∥CD C E D A F B 1 2 3 证明：∵∠1=∠2 （已知） ∠1=∠3 （对顶角相等） ∴ ∠2=∠3 （等量代换） ∴AB∥CD（同位角相等，两直线平行） 结论 ：两条直线被第三条直线所截， 如果内错角相等，那么这两条直线平行. 简称：内错角相等，两直线平行. 例2 已知直线AB与CD被直线EF所截， 且∠1与∠2互补. 试证明 AB∥CD C E D A F B 1 2 3 证明：∵∠1与∠2互补 （已知） ∠1与∠3互补 （邻补角定义） ∴ ∠2=∠3 （同角的补角相等） ∴AB∥CD（内错角相等，两直线平行） 结论 ：两条直线被第三条直线所截，如 果同旁内角互补，那么这两条直线平行. 简称：同旁内角互补，两直线平行. 平行线的判定 1. 判定公理 同位角相等，两直线平行. 2. 判定定理 内错角相等，两直线平行. 3. 判定定理 同旁内角互补，两直线平行. 巩固训练 1.已知直线a、b，任意画一 条直线c，使它与a、b都相 交，∠1=65°，∠2=65°， 那么a∥b，为什么？ a b c 1 2 2.如图，直线AB、CD被直线EF所截. （1）量得∠1=80°，∠2=80°，就可 以判定AB∥CD.它的根据是什么？ （2）量得∠3=100°，∠4=100°，就 可以判定AB∥CD.它的根据是什么？ （3）量得∠1=80°，∠3=100°，就可 以判定AB∥CD.它的根据是什么 A C E F B D 1 3 2 4 3. 如图，AB、CD、EF、HG都是直线， 根据下列已知条件，分别说出直线 AB∥CD的理由 A C E F G B H D 1 4 2 3 5 8 6 7 10 12 9 11 (A)∠1=∠5 (C) ∠1=∠7 (B) ∠4=∠6 4. 如图，根据下列条件，可判断那两条直线平行？ 为什么？ (1) ∠B=∠1; (2) ∠D=∠1; (3) ∠2+∠3=180° A F D B E C 13 2解 (1)∵∠B=∠1 (已知) ∴AB∥CD(同位角相等，两直线平行) (2) ∵∠D=∠1 (已知) ∴AB∥CD(内错角相等，两直线平行) (3) ∵ ∠2+∠3=180° (已知) ∴AE∥CF(同旁内角互补，两直线平行) 提高性训练 例3. 已知∠1=40°，∠2 =55°，∠3=85°. 求证: 直线AB∥CD 1 2 3 A B C D 4 5 小 结 • 本节重点 • 平行线的判定公理与判定定理 • 学会简单的推理论证 例4 已知AB⊥AC,CD⊥AC， 求证：AB∥CD 证明：∵ AB⊥AC,CD⊥AC （已知） ∴∠BAC= ∠ACD=90° （垂直定义） ∴ ∠BAC+ ∠ACD =180° （等式的性质） ∴直线AB∥CD（同旁内角 互补，两直线平行） A B C D 结论 ：垂直于同一直线的两直线平行 延伸训练