四川省成都市高新区2019-2020学年第二学期期末考试七年级数学试卷 （解析版）(1) 27页

‎2019-2020学年四川省成都市高新区七年级第二学期期末数学试卷 一、选择题 ‎1．下列计算正确的是（　　）‎ A．a3•a2＝a6 B．b4•b4＝2b4 C．x5+x5＝x10 D．y7•y＝y8‎ ‎2．新冠疫情发生以来，各地根据教育部“停课不停教，停课不停学”的相关通知精神，积极开展线上教学．下列在线学习平台的图标中，是轴对称图形的是（　　）‎ A． B． ‎ C． D．‎ ‎3．空气的密度是0.001293g/cm3，0.001293用科学记数法表示为（　　）‎ A．1.293×103 B．1.293×10﹣3 C．1.293×10﹣4 D．12.93×10﹣4‎ ‎4．下列长度的三根小木棒，能摆成三角形的是（　　）‎ A．3cm，4cm，5cm B．8cm，7cm，15cm ‎ C．15cm，13cm，1cm D．5cm，5cm，11cm ‎5．下列能判断AB∥CD的是（　　）‎ A．∠1＝∠4 B．∠2＝∠3 ‎ C．∠A＝∠C D．∠A+∠ABC＝180°‎ ‎6．下列事件为必然事件的是（　　）‎ A．打开电视，正在播放新闻 ‎ B．买一张电影票，座位号是奇数号 ‎ C．任意画一个三角形，其内角和是180° ‎ D．掷一枚质地均匀的硬币，正面朝上 ‎7．如图，在△ABC和△DEF中，∠B＝∠DEF，AB＝DE，添加下列一个条件后，仍然不能证明△ABC≌△DEF，这个条件是（　　）‎ A．∠A＝∠D B．BC＝EF C．∠ACB＝∠F D．AC＝DF ‎8．下列整式运算正确的是（　　）‎ A．（a﹣b）2＝a2﹣b2 B．（a+2）（a﹣2）＝a2﹣2 ‎ C．（a+2）（a﹣2）＝a2﹣4 D．（a+2b2）＝a2+2ab+4b2‎ ‎9．如图，在△ABC中，∠B＝30°，若AB∥CD，CB平分∠ACD，则∠ACD的度数为（　　）‎ A．30° B．40° C．60° D．90°‎ ‎10．小明站在离家不远的公共汽车站等车．能最好地刻画等车这段时间离家距离与时间的关系图象是（　　）‎ A． B． ‎ C． D．‎ 二、填空题（本大题共4个小题，每小题4分，共16分，答案写在答题卡上）‎ ‎11．计算：（﹣x3y）2＝　 　．‎ ‎12．等腰三角形的一个底角为50°，则它的顶角的度数为　 　．‎ ‎13．已知：a+b＝3，则代数式a2+2ab+b2的值为　 　．‎ ‎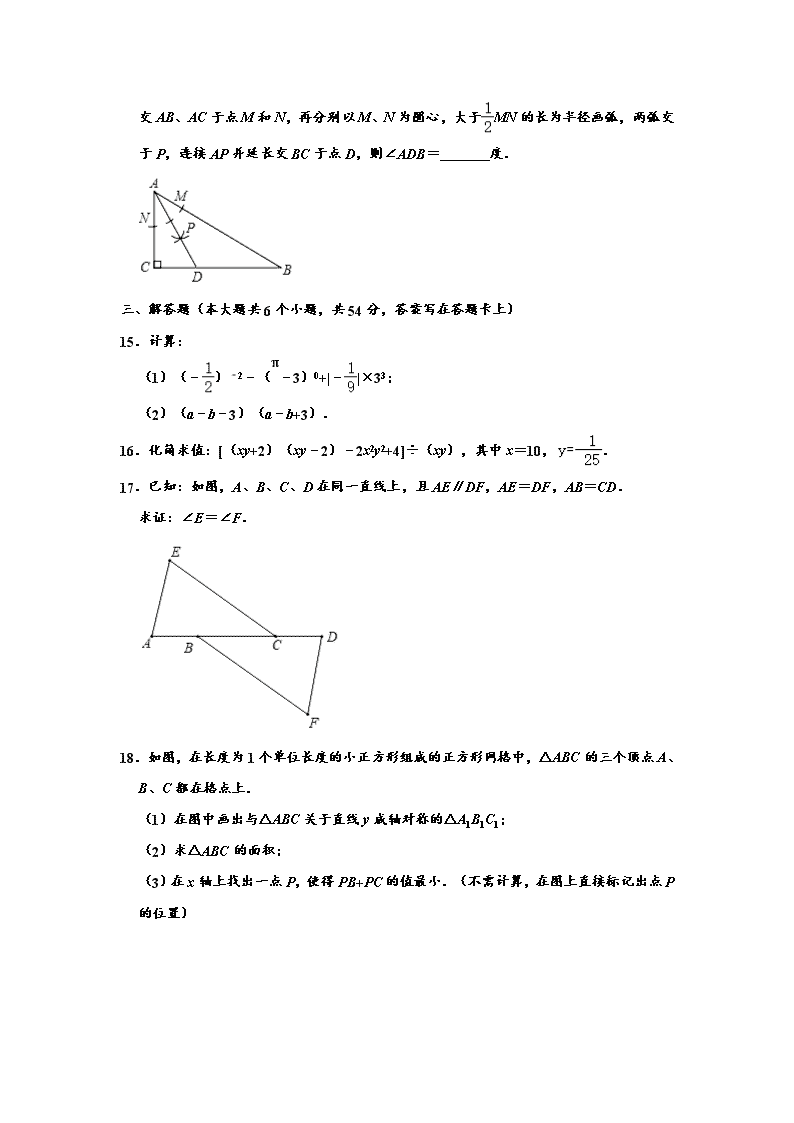14．如图，在△ABC中，∠C＝90°，∠B＝30°，以点A 为圆心，任意长为半径画弧分别交AB、AC于点M和N，再分别以M、N为圆心，大于MN的长为半径画弧，两弧交于P，连接AP并延长交BC于点D，则∠ADB＝　 　度．‎ 三、解答题（本大题共6个小题，共54分，答案写在答题卡上）‎ ‎15．计算：‎ ‎（1）（﹣）﹣2﹣（π﹣3）0+|﹣|×33；‎ ‎（2）（a﹣b﹣3）（a﹣b+3）．‎ ‎16．化简求值：[（xy+2）（xy﹣2）﹣2x2y2+4]÷（xy），其中x＝10，．‎ ‎17．已知：如图，A、B、C、D在同一直线上，且AE∥DF，AE＝DF，AB＝CD．‎ 求证：∠E＝∠F．‎ ‎18．如图，在长度为1个单位长度的小正方形组成的正方形网格中，△ABC的三个顶点A、B、C都在格点上．‎ ‎（1）在图中画出与△ABC关于直线y成轴对称的△A1B1C1；‎ ‎（2）求△ABC的面积；‎ ‎（3）在x轴上找出一点P，使得PB+PC的值最小．（不需计算，在图上直接标记出点P的位置）‎ ‎19．我市一水果批发市场某商家批发苹果采取分段计价的方式，其价格如下表：‎ 购买苹果数x（千克）‎ 不超过50千克的部分 超过50千克的部分 每千克价格（元）‎ ‎10‎ ‎8‎ ‎（1）小刚购买苹果40千克，应付多少元？‎ ‎（2）若小刚购买苹果x千克，用去了y元．分别写出当0≤x≤50和x＞50时，y与x的关系式；‎ ‎（3）计算出小刚若一次性购买80千克所付的费用比分两次共购买80千克（每次都购买40千克）所付的费用少多少元？‎ ‎20．如图，△ABC和△DEF是两个等腰直角三角形，∠BAC＝∠DFE＝90°，AB＝AC，FD＝FE，△DEF的顶点E在边BC上移动，在移动过程中，线段DE与线段AB相交于点P，线段EF与线段CA相交于点Q．‎ ‎（1）如图1，当E为BC中点，且BP＝CQ时，求证：△BPE≌△CQE；‎ ‎（2）如图2，当ED经过点A，且BE＝CQ时，求∠EAQ的度数；‎ ‎（3）如图3，当E为BC中点，连接AE、PQ，若AP＝3，AQ＝4，PQ＝5，求AC的长．‎ 一、填空题（本大题共5个小题，每小题4分，共20分，答案写在答题卡上）B卷（共50分）‎ ‎21．已知当x＝1时，2ax2+bx的值为3，则当x＝2时，ax2+bx的值为　 　．‎ ‎22．在开展“全民阅读”活动中，某校为了解全校1500名学生课外阅读的情况，随机调查了50名学生一周的课外阅读时间，并绘制成如图所示的条形统计图．根据图中数据，估计该校1500名学生一周的课外阅读时间不少于7小时的人数是　 　．‎ ‎23．三角形中，如果有一个内角是另外一个内角的3倍，我们把这个三角形叫做“三倍角三角形”．在一个“三倍角三角形”中有一个内角为60°，则另外两个角分别为　 　．‎ ‎24．如图，在△ABC中，AB＝AC，D为线段BC上一动点（不与点B、C重合），连接AD，作∠DAE＝∠BAC，且AD＝AE，连接CE．‎ ‎（1）如图1，当CE∥AB时，若∠BAD＝35°，则∠DEC　 　度；‎ ‎（2）如图2，设∠BAC＝α （90°＜α＜180°），在点D运动过程中，当DE⊥BC时，∠DEC＝　 　．（用含α的式子表示）‎ ‎25．如图，点C为线段AB的中点，以BC为边作正方形BCDE，点F、点G分别在边DE、DC上，且满足DF＝DG，连接BF，连接AG并延长交BF于点H，连接DH．以下结论：‎ ‎①△ACG≌△BEF；‎ ‎②HD＝HG；‎ ‎③AH⊥BF；‎ ‎④∠DHG＝45°．‎ 其中正确的有　 　（填序号）．‎ 二、解答题（本大题共3个小题，共30分，答案写在答题卡上）‎ ‎26．（1）已知：a（a+1）﹣（a2+b）＝3，a（a+b）+b（b﹣a）＝13，求代数式ab的值．‎ ‎（2）已知等腰△ABC的两边分别为a、b，且a、b满足a2+b2﹣6a﹣14b+58＝0，求△ABC的周长．‎ ‎27．小张和小王是同一单位在A、B两市的同事，已知A、B两市相距400km，周六上午小王从B市出发，开车匀速前往A市的公司开会，1小时后小张从A市的公司出发，沿同一路线开车匀速前往B市，小张行驶了一段路程后，得知小王要到A市的公司开会，便立即加速返回公司（折返的时间忽略不计）．已知小张返回时的速度比去时的速度每小时快20km．两人距B市的距离y（km）与小张行驶时间x（h）间的关系如图所示，请结合图象解答下列问题：‎ ‎（1）小王的速度为　 　km/h，a的值为　 　；‎ ‎（2）求小张加速前的速度和b的值；‎ ‎（3）在小张从出发到回到A市的公司过程中，当x为何值时，两人相距20km？‎ ‎28．已知：△ABC为等边三角形．‎ ‎（1）如图1，点D、E分别为边BC、AC上的点，且BD＝CE．‎ i）求证：△ABD≌△BCE；‎ ii）求∠AFE的度数；‎ ‎（2）如图2，点D为△ABC外一点，BA、CD的延长线交于点E，连接AD，已知∠BDC＝60°，且AD＝2，CD＝5，求BD的长；‎ ‎（3）如图3，线段DB的长为3，线段DC的长为2，连接BC，以BC为边作等边△ABC，连接AD，直接写出当线段AD取最大值与最小值时∠BDC的度数．‎ 参考答案 一、选择题（本大题共10个小题，每小题3分，共30分，每小题均有四个选项，其中只有一项符合题目要求，答案涂在答题卡上）‎ ‎1．下列计算正确的是（　　）‎ A．a3•a2＝a6 B．b4•b4＝2b4 C．x5+x5＝x10 D．y7•y＝y8‎ ‎【分析】根据合并同类项的法则，只把系数相加减，字母与字母的指数不变；同底数幂相乘，底数不变指数相加解答．‎ 解：A、应为a3•a2＝a5，故本选项错误；‎ B、应为b4•b4＝b8，故本选项错误；‎ C、应为x5+x5＝2x5，故本选项错误；‎ D、y7•y＝y8，正确．‎ 故选：D．‎ ‎2．新冠疫情发生以来，各地根据教育部“停课不停教，停课不停学”的相关通知精神，积极开展线上教学．下列在线学习平台的图标中，是轴对称图形的是（　　）‎ A． B． ‎ C． D．‎ ‎【分析】根据“如果一个图形沿一条直线折叠，直线两旁的部分能够互相重合，这个图形叫做轴对称图形”判断即可得．‎ 解：四个图形中是轴对称图形的只有A选项，‎ 故选：A．‎ ‎3．空气的密度是0.001293g/cm3，0.001293用科学记数法表示为（　　）‎ A．1.293×103 B．1.293×10﹣3 C．1.293×10﹣4 D．12.93×10﹣4‎ ‎【分析】绝对值小于1的正数也可以利用科学记数法表示，一般形式为a×10﹣n ‎，与较大数的科学记数法不同的是其所使用的是负指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．‎ 解：0.001293＝1.293×10﹣3，‎ 故选：B．‎ ‎4．下列长度的三根小木棒，能摆成三角形的是（　　）‎ A．3cm，4cm，5cm B．8cm，7cm，15cm ‎ C．15cm，13cm，1cm D．5cm，5cm，11cm ‎【分析】根据三角形的三边关系对各选项进行逐一分析即可．‎ 解：A、3+4＝7＞5，能构成三角形，故本选项符合题意；‎ B、8+7＝15，不能构成三角形，故本选项不符合题意；‎ C、1+13＝14＜15，不能构成三角形，故本选项不符合题意；‎ D、5+5＝10＜11，不能构成三角形，故本选项不符合题意．‎ 故选：A．‎ ‎5．下列能判断AB∥CD的是（　　）‎ A．∠1＝∠4 B．∠2＝∠3 ‎ C．∠A＝∠C D．∠A+∠ABC＝180°‎ ‎【分析】根据两条直线被第三条所截，如果内错角相等，那么这两条直线平行可得答案．‎ 解：A、∵∠1＝∠4，‎ ‎∴AB∥CD，故A选项符合题意；‎ B、∵∠2＝∠3，‎ ‎∴AD∥CB，故B选项不符合题意；‎ C、∵∠A＝∠C，‎ 无法判断AB∥CD，故C选项不符合题意；‎ D、∵∠A+∠ABC＝180°，‎ ‎∴AD∥CB，故D选项不符合题意；‎ 故选：A．‎ ‎6．下列事件为必然事件的是（　　）‎ A．打开电视，正在播放新闻 ‎ B．买一张电影票，座位号是奇数号 ‎ C．任意画一个三角形，其内角和是180° ‎ D．掷一枚质地均匀的硬币，正面朝上 ‎【分析】根据事件发生的可能性大小判断．‎ 解：A、打开电视，正在播放新闻，是随机事件；‎ B、买一张电影票，座位号是奇数号，是随机事件；‎ C、任意画一个三角形，其内角和是180°，是必然事件；‎ D、掷一枚质地均匀的硬币，正面朝上，是随机事件；‎ 故选：C．‎ ‎7．如图，在△ABC和△DEF中，∠B＝∠DEF，AB＝DE，添加下列一个条件后，仍然不能证明△ABC≌△DEF，这个条件是（　　）‎ A．∠A＝∠D B．BC＝EF C．∠ACB＝∠F D．AC＝DF ‎【分析】根据全等三角形的判定，利用ASA、SAS、AAS即可得答案．‎ 解：∵∠B＝∠DEF，AB＝DE，‎ ‎∴添加∠A＝∠D，利用ASA可得△ABC≌△DEF；‎ ‎∴添加BC＝EF，利用SAS可得△ABC≌△DEF；‎ ‎∴添加∠ACB＝∠F，利用AAS可得△ABC≌△DEF；‎ 故选：D．‎ ‎8．下列整式运算正确的是（　　）‎ A．（a﹣b）2＝a2﹣b2 B．（a+2）（a﹣2）＝a2﹣2 ‎ C．（a+2）（a﹣2）＝a2﹣4 D．（a+2b2）＝a2+2ab+4b2‎ ‎【分析】根据各个选项中的式子，可以计算出正确的结果，从而可以解答本题．‎ 解：∵（a﹣b）2＝a2﹣2ab+b2，故选项A错误；‎ ‎∵（a+2）（a﹣2）＝a2﹣4，故选项B错误；‎ ‎∵（a+2）（a﹣2）＝a2﹣4，故选项C正确；‎ ‎∵（a+2b2）＝a2+4ab+4b2，故选项D错误；‎ 故选：C．‎ ‎9．如图，在△ABC中，∠B＝30°，若AB∥CD，CB平分∠ACD，则∠ACD的度数为（　　）‎ A．30° B．40° C．60° D．90°‎ ‎【分析】根据AB∥CD，可得∠BCD＝∠B＝30°，然后根据CB平分∠ACD，可得∠ACD＝2∠BCD＝60°．‎ 解：如图，∵AB∥CD，∠B＝30°，‎ ‎∴∠BCD＝∠B＝30°，‎ ‎∵CB平分∠ACD，‎ ‎∴∠ACD＝2∠BCD＝60°．‎ 故选：C．‎ ‎10．小明站在离家不远的公共汽车站等车．能最好地刻画等车这段时间离家距离与时间的关系图象是（　　）‎ A． B． ‎ C． D．‎ ‎【分析】在车站等车，离家的距离不变，从而得出答案．‎ 解：∵小明站在离家不远的公共汽车站等车，‎ ‎∴这段时间离家距离不随时间的变化而变化，‎ 故选：B．‎ 二、填空题（本大题共4个小题，每小题4分，共16分，答案写在答题卡上）‎ ‎11．计算：（﹣x3y）2＝　x6y2　．‎ ‎【分析】根据积的乘方法则求出即可．‎ 解：（﹣x3y）2＝x6y2，‎ 故答案为：x6y2．‎ ‎12．等腰三角形的一个底角为50°，则它的顶角的度数为　80°　．‎ ‎【分析】本题给出了一个底角为50°，利用等腰三角形的性质得另一底角的大小，然后利用三角形内角和可求顶角的大小．‎ 解：∵等腰三角形底角相等，‎ ‎∴180°﹣50°×2＝80°，‎ ‎∴顶角为80°．‎ 故填80°．‎ ‎13．已知：a+b＝3，则代数式a2+2ab+b2的值为　9　．‎ ‎【分析】根据完全平分公式：（a+b）2＝a2+2ab+b2，即可解答．‎ 解：因为a+b＝3，‎ 所以a2+2ab+b2＝（a+b）2＝32＝9．‎ 故答案为：9．‎ ‎14．如图，在△ABC中，∠C＝90°，∠B＝30°，以点A为圆心，任意长为半径画弧分别交AB、AC于点M和N，再分别以M、N为圆心，大于MN的长为半径画弧，两弧交于P，连接AP并延长交BC于点D，则∠ADB＝　120　度．‎ ‎【分析】利用角平分线的定义可以推知∠CAD＝30°，根据三角形外角的性质即可得到结论．‎ 解：∵在△ABC中，∠C＝90°，∠B＝30°，‎ ‎∴∠CAB＝60°，‎ 又∵AD是∠BAC的平分线，‎ ‎∴∠CAD＝∠BAD＝∠CAB＝30°，‎ ‎∴∠ADB＝90°+30°＝120°，‎ 故答案为：120；‎ 三、解答题（本大题共6个小题，共54分，答案写在答题卡上）‎ ‎15．计算：‎ ‎（1）（﹣）﹣2﹣（π﹣3）0+|﹣|×33；‎ ‎（2）（a﹣b﹣3）（a﹣b+3）．‎ ‎【分析】（1）根据负指数幂、零指数幂、绝对值、有理数的乘方的运算法则计算即可；‎ ‎（2）先应用平方差公式计算，再运用完全平方公式计算即可．‎ 解：（1）（﹣）﹣2﹣（π﹣3）0+|﹣|×33‎ ‎＝4﹣1+×27‎ ‎＝3+3‎ ‎＝6；‎ ‎（2）（a﹣b﹣3）（a﹣b+3）‎ ‎＝[（a﹣b）﹣3][（a﹣b）+3]‎ ‎＝（a﹣b）2﹣32‎ ‎＝a2﹣2ab+b2﹣9．‎ ‎16．化简求值：[（xy+2）（xy﹣2）﹣2x2y2+4]÷（xy），其中x＝10，．‎ ‎【分析】原式被除数括号中第一项利用平方差公式化简，合并后利用多项式除以单项式法则计算，得到最简结果，将x与y的值代入计算即可求出值．‎ 解：原式＝（x2y2﹣4﹣2x2y2+4）÷（xy）＝（﹣x2y2）÷（xy）＝﹣xy，‎ 当x＝10，y＝﹣时，原式＝﹣10×（﹣）＝．‎ ‎17．已知：如图，A、B、C、D在同一直线上，且AE∥DF，AE＝DF，AB＝CD．‎ 求证：∠E＝∠F．‎ ‎【分析】根据AE∥DF，可以得到∠A＝∠D，再根据AB＝CD，可以得到AC＝DB，然后即可证明△EAC和△FDB全等，从而可以得到∠E＝∠F．‎ ‎【解答】证明：∵AE∥DF，‎ ‎∴∠A＝∠D，‎ ‎∵AB＝CD，‎ ‎∴AB+BC＝CD+BC，‎ ‎∴AC＝DB，‎ 在△EAC和△FDB中，‎ ‎，‎ ‎∴△EAC≌△FDB（SAS），‎ ‎∴∠E＝∠F．‎ ‎18．如图，在长度为1个单位长度的小正方形组成的正方形网格中，△ABC的三个顶点A、B、C都在格点上．‎ ‎（1）在图中画出与△ABC关于直线y成轴对称的△A1B1C1；‎ ‎（2）求△ABC的面积；‎ ‎（3）在x轴上找出一点P，使得PB+PC的值最小．（不需计算，在图上直接标记出点P的位置）‎ ‎【分析】（1）依据轴对称的性质，即可得到与△ABC关于直线y成轴对称的△A1B1C1；‎ ‎（2）依据割补法进行计算，即可得出△ABC的面积；‎ ‎（3）作点B关于x轴的对称点B'，连接B'C交x轴于P，则PB+PC的值最小．‎ 解：（1）如图所示，△A1B1C1即为所求；‎ ‎（2）△ABC的面积＝3×3﹣×2×3﹣×1×2﹣×1×3＝；‎ ‎（3）如图所示，点P即为所求．‎ ‎19．我市一水果批发市场某商家批发苹果采取分段计价的方式，其价格如下表：‎ 购买苹果数x（千克）‎ 不超过50千克的部分 超过50千克的部分 每千克价格（元）‎ ‎10‎ ‎8‎ ‎（1）小刚购买苹果40千克，应付多少元？‎ ‎（2）若小刚购买苹果x千克，用去了y元．分别写出当0≤x≤50和x＞50时，y与x的关系式；‎ ‎（3）计算出小刚若一次性购买80千克所付的费用比分两次共购买80千克（每次都购买40千克）所付的费用少多少元？‎ ‎【分析】（1）根据题意和表格中的数据，可以计算出小刚购买苹果40千克，应付多少元；‎ ‎（2）根据表格中的数据，可以分别写出当0≤x≤50和x＞50时，y与x的关系式；‎ ‎（3）根据（2）中的函数关系式，可以求得两种情况下的花费，然后作差即可解答本题．‎ 解：（1）由表格可得，‎ ‎40×10＝400（元），‎ 答：小刚购买苹果40千克，应付400元；‎ ‎（2）由题意可得，‎ 当0≤x≤50时，y与x的关系式是y＝10x，‎ 当x＞50时，y与x的关系式是y＝10×50+8（x﹣50）＝8x+100，‎ 即当x＞50时，y与x的关系式是y＝8x+100；‎ ‎（3）小刚若一次性购买80千克所付的费用为：8×80+100＝740（元），‎ 分两次共购买80千克（每次都购买40千克）所付的费用为：40×10×2＝800（元），‎ ‎800﹣740＝60（元），‎ 答：小刚若一次性购买80千克所付的费用比分两次共购买80千克（每次都购买40千克）所付的费用少60元．‎ ‎20．如图，△ABC和△DEF是两个等腰直角三角形，∠BAC＝∠DFE＝90°，AB＝AC，FD＝FE，△DEF的顶点E在边BC上移动，在移动过程中，线段DE与线段AB相交于点P，线段EF与线段CA相交于点Q．‎ ‎（1）如图1，当E为BC中点，且BP＝CQ时，求证：△BPE≌△CQE；‎ ‎（2）如图2，当ED经过点A，且BE＝CQ时，求∠EAQ的度数；‎ ‎（3）如图3，当E为BC中点，连接AE、PQ，若AP＝3，AQ＝4，PQ＝5，求AC的长．‎ ‎【分析】（1）由△ABC是等腰直角三角形，易得∠B＝∠C＝45°，AB＝AC，又由AP＝AQ，E是BC的中点，利用SAS，可证得：△BPE≌△CQE；‎ ‎（2）证明△ABE≌△ECQ（AAS），由全等三角形的性质得出AE＝EQ ‎，由三角形内角和定理可求出答案；‎ ‎（3）在CQ上截取CH，使得CH＝AP，连接EH，证明△CHE≌△APE（SAS），由全等三角形的性质得出HE＝PE，∠CEH＝∠AEP，证明△HEQ≌△PEQ（SAS），得出HQ＝PQ，则可求出答案．‎ ‎【解答】（1）证明：∵△ABC是等腰直角三角形，‎ ‎∴∠B＝∠C＝45°，AB＝AC，‎ ‎∵E是BC的中点，‎ ‎∴BE＝CE，‎ 在△BPE和△CQE中，‎ ‎∵，‎ ‎∴△BPE≌△CQE（SAS）；‎ ‎（2）解：∵∠AEQ＝45°，∠B＝45°，‎ ‎∴∠AEB+∠QEC＝135°，∠AEB+∠BAE＝135°，‎ ‎∴∠QEC＝∠BAE，‎ 又∵∠B＝∠C，BE＝CQ，‎ ‎∴△ABE≌△ECQ（AAS），‎ ‎∴AE＝EQ，‎ ‎∴∠EAQ＝∠EQA＝．‎ ‎（3）在CQ上截取CH，使得CH＝AP，连接EH，‎ 由（1）知AE＝CE，∠C＝∠EAP＝45°，‎ ‎∵在△CHE与△APE中：‎ ‎，‎ ‎∴△CHE≌△APE（SAS），‎ ‎∴HE＝PE，∠CEH＝∠AEP，‎ ‎∴∠HEQ＝∠AEC﹣∠CEH﹣∠AEQ＝∠AEC﹣∠AEP﹣∠AEQ＝∠AEC﹣∠PEF＝90°﹣45°＝45°，‎ ‎∴∠HEQ＝∠PEQ＝45°，‎ ‎∵在△HEQ与△PEQ中：‎ ‎，‎ ‎∴△HEQ≌△PEQ（SAS），‎ ‎∴HQ＝PQ，‎ ‎∴AC＝AQ+QH+CH＝AQ+PQ+AP＝4+5+3＝12．‎ 一、填空题（本大题共5个小题，每小题4分，共20分，答案写在答题卡上）B卷（共50分）‎ ‎21．已知当x＝1时，2ax2+bx的值为3，则当x＝2时，ax2+bx的值为　6　．‎ ‎【分析】将x＝1代入2ax2+bx＝3得2a+b＝3，然后将x＝2代入ax2+bx得4a+2b＝2（2a+b），之后整体代入即可．‎ 解：将x＝1代入2ax2+bx＝3得2a+b＝3，‎ 将x＝2代入ax2+bx得4a+2b＝2（2a+b），‎ ‎∵2a+b＝3，‎ ‎∴原式＝2×3＝6．‎ 故答案为：6．‎ ‎22．在开展“全民阅读”活动中，某校为了解全校1500名学生课外阅读的情况，随机调查了50名学生一周的课外阅读时间，并绘制成如图所示的条形统计图．根据图中数据，估计该校1500名学生一周的课外阅读时间不少于7小时的人数是　600　．‎ ‎【分析】用所有学生数乘以课外阅读时间不少于7小时的人数所占的百分比即可．‎ 解：该校1500名学生一周的课外阅读时间不少于7小时的人数是1500×＝600人，‎ 故答案为：600．‎ ‎23．三角形中，如果有一个内角是另外一个内角的3倍，我们把这个三角形叫做“三倍角三角形”．在一个“三倍角三角形”中有一个内角为60°，则另外两个角分别为　100°，20°或90°，30°　．‎ ‎【分析】分三种情形讨论求解即可解决问题．‎ 解：在△ABC中，不妨设∠A＝60°．‎ ‎①若∠A＝3∠C，则∠C＝20°，∠B＝100°．‎ ‎②若∠C＝3∠A，则∠A＝180°（不合题意）．‎ ‎③若∠B＝3∠C，则∠B＝90°，∠C＝30°，‎ 综上所述，另外两个角的度数为100°，20°或90°，30°．‎ 故答案为：100°，20°或90°，30°．‎ ‎24．如图，在△ABC中，AB＝AC，D为线段BC上一动点（不与点B、C重合），连接AD，作∠DAE＝∠BAC，且AD＝AE，连接CE．‎ ‎（1）如图1，当CE∥AB时，若∠BAD＝35°，则∠DEC　25　度；‎ ‎（2）如图2，设∠BAC＝α （90°＜α＜180°），在点D运动过程中，当DE⊥BC时，∠DEC＝　α﹣90°　．（用含α的式子表示）‎ ‎【分析】（1）根据已知条件得到∠BAD＝∠CAE，根据全等三角形的性质得到∠B＝∠ACE，根据平行线的想知道的∠BAC＝∠ACE，推出△ABC是等边三角形，得到∠BAC＝∠DAE＝∠ACB＝∠ACE＝60°，求得△DAE是等边三角形，于是得到结论；‎ ‎（2）根据等腰三角形的性质得到∠B＝∠ACB＝（180°﹣α）＝90°﹣‎ ‎，根据全等三角形的性质得到∠B＝∠ACE＝90°﹣，求得∠DCE＝2（90°﹣）＝180°﹣α，根据三角形的内角和即可得到结论．‎ 解：（1）∵∠DAE＝∠BAC，‎ ‎∴∠BAC﹣∠CAD＝∠DAE﹣∠CAD，‎ 即∠BAD＝∠CAE，‎ ‎∴△ABD≌△ACE（SAS），‎ ‎∴∠B＝∠ACE，‎ ‎∵CE∥AB，‎ ‎∴∠BAC＝∠ACE，‎ ‎∴∠BAC＝∠B，‎ ‎∴AC＝BC，‎ ‎∴△ABC是等边三角形，‎ ‎∴∠BAC＝∠DAE＝∠ACB＝∠ACE＝60°，‎ ‎∴△DAE是等边三角形，‎ ‎∴∠AED＝60°，‎ ‎∴∠DEC＝180°﹣35°﹣60°﹣60°＝25°，‎ 故答案为：25；‎ ‎（2）连接CE，‎ ‎∵∠BAC＝α，AB＝AC，‎ ‎∴∠B＝∠ACB＝（180°﹣α）＝90°﹣，‎ ‎∵∠DAE＝∠BAC，‎ ‎∴∠BAC﹣∠CAD＝∠DAE﹣∠CAD，‎ 即∠BAD＝∠CAE，‎ ‎∴△ABD≌△ACE（SAS），‎ ‎∴∠B＝∠ACE＝90°﹣，‎ ‎∴∠DCE＝2（90°﹣）＝180°﹣α，‎ ‎∵DE⊥BC，‎ ‎∴∠CDE＝90°，‎ ‎∴∠DEC＝90°﹣∠DCE＝α﹣90°．‎ 故答案为：α﹣90°．‎ ‎25．如图，点C为线段AB的中点，以BC为边作正方形BCDE，点F、点G分别在边DE、DC上，且满足DF＝DG，连接BF，连接AG并延长交BF于点H，连接DH．以下结论：‎ ‎①△ACG≌△BEF；‎ ‎②HD＝HG；‎ ‎③AH⊥BF；‎ ‎④∠DHG＝45°．‎ 其中正确的有　①③④　（填序号）．‎ ‎【分析】由“SAS”可证△ACG≌△BEF，可得判定①；由全等三角形的性质可得∠A＝∠EBF，∠AGC＝∠BFE，由余角的性质可得∠AHB＝90°，可判断③；过点D作DN⊥BF于N，DM⊥AH于H，由“AAS”可证△DHN≌△DHM，可得∠DHM＝∠DHN＝45°，可判断④，若若DH＝DG，可求∠A＝22.5°，由点F、点G分别在边DE、DC上，则∠A不是定值，可判断②，即可求解．‎ 解：∵点C为线段AB的中点，‎ ‎∴AC＝BC，‎ ‎∵四边形BCDE是正方形，‎ ‎∴DE＝DC＝BC＝BE＝AC，∠E＝∠DCB＝90°，‎ 又∵DF＝DG，‎ ‎∴CG＝EF，‎ 又∵∠E＝∠ACG＝90°，‎ ‎∴△ACG≌△BEF（SAS），故①正确，‎ ‎∴∠A＝∠EBF，∠AGC＝∠BFE，‎ ‎∵∠EBF+∠FBC＝90°，‎ ‎∴∠A+∠FBC＝90°，‎ ‎∴∠AHB＝90°，‎ ‎∴AH⊥BF；故③正确，‎ 过点D作DN⊥BF于N，DM⊥AH于H，‎ ‎∵∠AGC＝∠BFE，‎ ‎∴∠DGM＝∠NFD，‎ 又∵∠DNF＝∠DMG＝90°，DF＝DG，‎ ‎∴△DHN≌△DHM（AAS），‎ ‎∴∠DHM＝∠DHN，‎ 又∵∠AHF＝90°，‎ ‎∴∠DHG＝45°，故④正确；‎ 若DH＝DG，∠DHG＝45°，‎ ‎∴∠HDG＝∠HGD＝67.5°，‎ ‎∴∠A＝22.5°，‎ ‎∵点F、点G分别在边DE、DC上，‎ ‎∴∠A不是定值，‎ ‎∴DH与HG不一定相等，故②错误．‎ 故答案为：①③④．‎ 二、解答题（本大题共3个小题，共30分，答案写在答题卡上）‎ ‎26．（1）已知：a（a+1）﹣（a2+b）＝3，a（a+b）+b（b﹣a）＝13，求代数式ab的值．‎ ‎（2）已知等腰△ABC的两边分别为a、b，且a、b满足a2+b2﹣6a﹣14b+58＝0，求△ABC的周长．‎ ‎【分析】（1）首先将已知条件化简，进而得出a2﹣2ab+b2＝9①，a2+b2＝13②，把②代入①可得结论；‎ ‎（2）首先利用勾股定理得出AC的长，进而得出AC和AB的长，即可得出BB′的长．‎ 解：（1）a（a+1）﹣（a2+b）＝3，‎ a2+a﹣a2﹣b＝3，‎ a﹣b＝3，‎ 两边同时平方得：a2﹣2ab+b2＝9①，‎ a（a+b）+b（b﹣a）＝13，‎ a2+ab+b2﹣ab＝13，‎ a2+b2＝13②，‎ 把②代入①得：13﹣2ab＝9，‎ ‎13﹣9＝2ab，‎ ‎∴ab＝2；‎ ‎（2）a2+b2﹣6a﹣14b+58＝0，‎ a2﹣6a+9+b2﹣14b+49＝0，‎ ‎（a﹣3）2+（b﹣7）2＝0，‎ ‎∴a﹣3＝0，b﹣7＝0，‎ ‎∴a＝3，b＝7，‎ 当3为腰时，三边为3，3，7，因为3+3＜7，不能构成三角形，此种情况不成立，‎ 当7为腰时，三边为7，7，3，能构成三角形，此时△ABC的周长＝7+7+3＝17．‎ ‎27．小张和小王是同一单位在A、B两市的同事，已知A、B两市相距400km，周六上午小王从B市出发，开车匀速前往A市的公司开会，1小时后小张从A市的公司出发，沿同一路线开车匀速前往B市，小张行驶了一段路程后，得知小王要到A市的公司开会，便立即加速返回公司（折返的时间忽略不计）．已知小张返回时的速度比去时的速度每小时快20km．两人距B市的距离y（km）与小张行驶时间x（h）间的关系如图所示，请结合图象解答下列问题：‎ ‎（1）小王的速度为　80　km/h，a的值为　4　；‎ ‎（2）求小张加速前的速度和b的值；‎ ‎（3）在小张从出发到回到A市的公司过程中，当x为何值时，两人相距20km？‎ ‎【分析】（1）根据函数图象中的数据，可以计算出小王的速度和a的值；‎ ‎（2）根据题意和（1）中的结果，可以计算出小张加速前的速度和b的值；‎ ‎（3）根据函数图象中的数据和题意，利用分类讨论的方法可以求得x的值．‎ 解：（1）由图象可得，‎ 小王的速度为：80÷1＝80（km/h），‎ a＝400÷80﹣1＝4，‎ 故答案为：80，4；‎ ‎（2）设小张加速前的速度为xkm/h，‎ ‎2.4x＝（x+20）×（4.4﹣2.4），‎ 解得，x＝100，‎ b＝400﹣2.4×100＝160，‎ 即小张加速前的速度为100km/h，b的值是160；‎ ‎（3）由题意可得，‎ 相遇前：100x+80（x+1）＝400﹣20‎ 解得，x＝，‎ 相遇后到小张返回前：100x+80（x+1）＝400+20‎ 解得，x＝，‎ 小张返回后到小王到达A市前：80×（x+1）＝（400﹣100×2.4）+（100+20）×（x﹣2.4）+20，‎ 解得，x＝4.7（舍去），‎ 小王到达A市到小张返回到A市前，‎ ‎（400﹣100×2.4）+（100+20）×（x﹣2.4）+20＝400，‎ 解得，x＝，‎ 由上可得，在小张从出发到回到A市的公司过程中，当x为何值时，两人相距20km．‎ ‎28．已知：△ABC为等边三角形．‎ ‎（1）如图1，点D、E分别为边BC、AC上的点，且BD＝CE．‎ i）求证：△ABD≌△BCE；‎ ii）求∠AFE的度数；‎ ‎（2）如图2，点D为△ABC外一点，BA、CD的延长线交于点E，连接AD，已知∠BDC＝60°，且AD＝2，CD＝5，求BD的长；‎ ‎（3）如图3，线段DB的长为3，线段DC的长为2，连接BC，以BC为边作等边△ABC，连接AD，直接写出当线段AD取最大值与最小值时∠BDC的度数．‎ ‎【分析】（1）i）根据SAS证明三角形全等即可．‎ ii）利用全等三角形的性质以及三角形的外角的性质即可解决问题．‎ ‎（2）如图2中，在DB上取一点J，使得CJ＝CD，利用全等三角形的性质证明BD＝AD+DC即可．‎ ‎（3）如图3中，以CD为边向外作等边△CDT，连接BT．构造全等三角形，证明BT＝AD，求出BT的取值范围即可解决问题．‎ ‎【解答】（1）i）证明：如图1中，∵△ABC是等边三角形，‎ ‎∴AB＝BC，∠ABD＝∠C＝60°，‎ ‎∵BD＝CE，‎ ‎∴△ABD≌△BCE（SAS）．‎ ii）解：如图1中，∵△ABD≌△BCE，‎ ‎∴∠BAD＝∠CBE，‎ ‎∴∠AFE＝∠FBA+∠BAD＝∠FBA+∠CBE＝∠CBA＝60°．‎ ‎（2）解：如图2中，在DB上取一点J，使得CJ＝CD，‎ ‎∵∠CDJ＝60°，CJ＝CD，‎ ‎∴△CDJ是等边三角形，‎ ‎∴∠JCD＝∠ACB＝60°，DJ＝DC＝CJ，‎ ‎∴∠BCJ＝∠ACD，‎ ‎∵CB＝CA，‎ ‎∴△BCJ≌△ACD（SAS），‎ ‎∴BJ＝AD，‎ ‎∴BD＝BJ+DJ＝AD+DC＝2+5＝7．‎ ‎（3）解：如图3中，以CD为边向外作等边△CDT，连接BT．‎ ‎∵CT＝CD，CB＝CA，∠TCD＝∠BCA＝60°，‎ ‎∴∠TCB＝∠DCA，‎ ‎∴△TCB≌△DCA（SAS），‎ ‎∴BT＝AD，‎ ‎∵CT＝CD＝2，BD＝3，‎ ‎∴3﹣2≤BT≤3+2，‎ ‎∴1≤BT≤5，‎ ‎∴1≤AD≤5．‎ ‎∴AD的最小值为1，最大值为5．‎ 当AD取最小值时，点T落在线段BD上，∠BDC＝60°，当AD取最大值时，点T落在BD的延长线上，∠BDC＝120°．‎