- 129.52 KB
- 2021-10-26 发布
- 1、本文档由用户上传,淘文库整理发布,可阅读全部内容。
- 2、本文档内容版权归属内容提供方,所产生的收益全部归内容提供方所有。如果您对本文有版权争议,请立即联系网站客服。
- 3、本文档由用户上传,本站不保证质量和数量令人满意,可能有诸多瑕疵,付费之前,请仔细阅读内容确认后进行付费下载。
- 网站客服QQ:403074932
12.3角的平分线的性质 (第2课时)
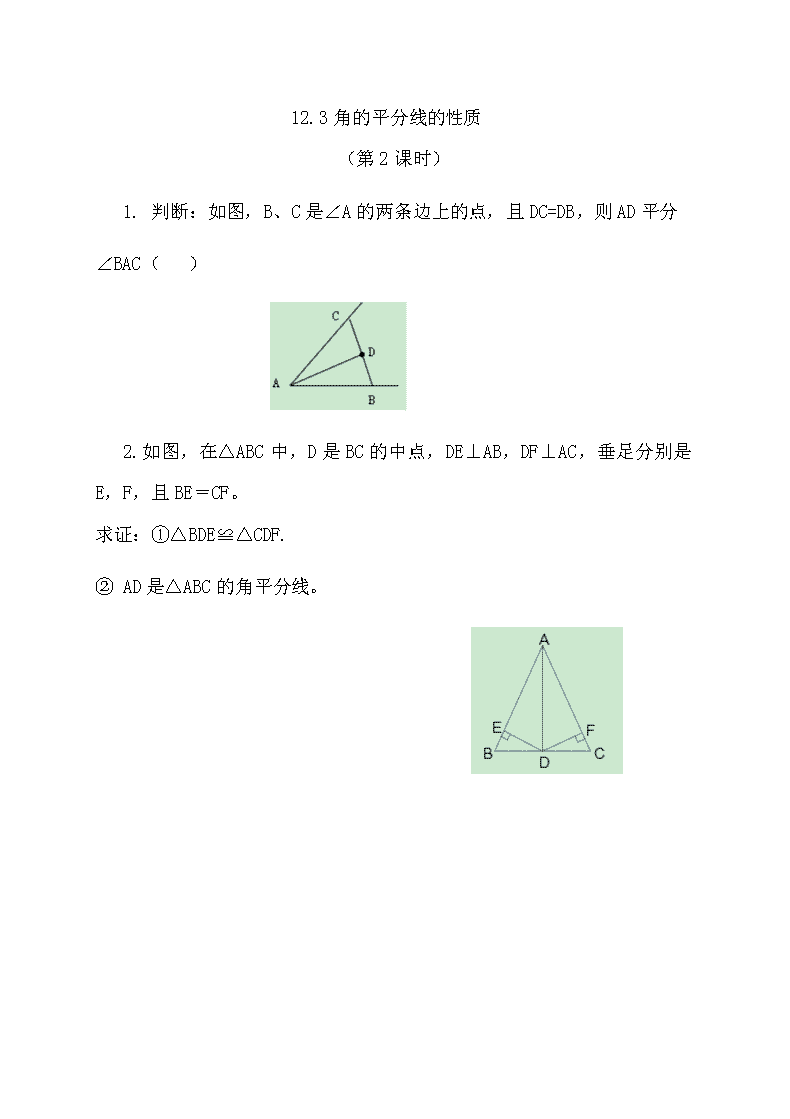
1. 判断:如图,B、C是∠A的两条边上的点,且DC=DB,则AD平分
∠BAC( )
2.如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F,且BE=CF。
求证:①△BDE≌△CDF.
② AD是△ABC的角平分线。
3.如图,已知△ABC的外角∠CBD和∠BCE的平分线相交于点F,
求证:点F在∠DAE的平分线上.
4. 如图,CD⊥AB,BE⊥AC,垂足分别为D,E,BE,CD相交于点O,OB=OC.
求证:AO平分∠BAC.
100米
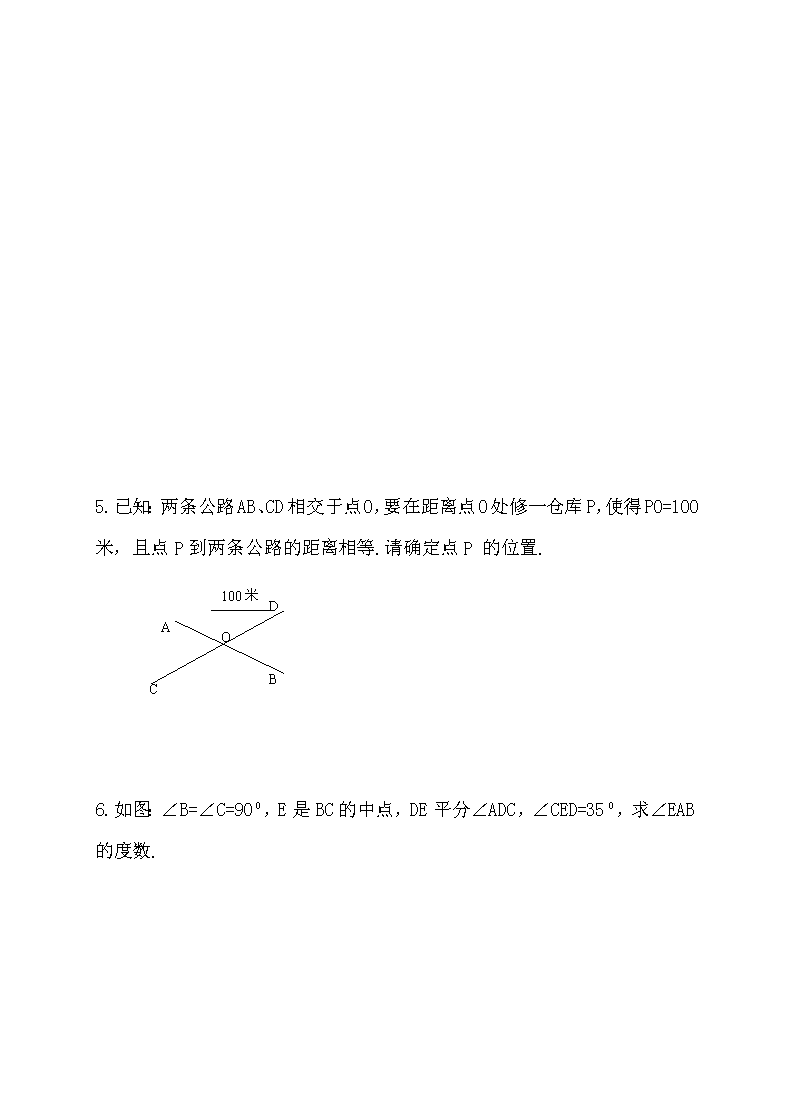
5.已知:两条公路AB、CD相交于点O,要在距离点O处修一仓库P,使得PO=100米,且点P到两条公路的距离相等.请确定点P 的位置.
A
B
C
D
O
6.如图:∠B=∠C=90,E是BC的中点,DE平分∠ADC,∠CED=35,求∠EAB的度数.
参考答案
1. 错
2. 由HL可证明△BDE≌△CDF,即DE=DF,所以AD是△ABC的角平分线.
3.过点F作BD、BC、CE的垂线,垂足分别是P、M、N,
BF、CF是∠CBD和∠BCE的平分线,
FP=FM=FN,即点F在∠DAE的平分线上.
4.由AAS可证明△BOD≌△COE,即OD=OE,所以AO平分∠BAC.
5.略,
6.过点E作AD的垂线,F为垂足,
∠B=∠C=90,DE平分∠ADC,
所以EC=EF,又因为EC=EB,
所以EF=EB,即AE平分∠DAB,可得∠AED=900,∠EAB=350.
相关文档
- 北师大-八年级(下)-数学期中2021-10-2636页
- 八年级下数学课件《分式的加减》课2021-10-2618页
- 八年级下数学课件《分式的加减》 2021-10-2613页
- 人教版物理八下175能源与可持续发2021-10-265页
- 八年级上物理课件八年级上册物理课2021-10-2621页
- (语文版)八年级语文上册第七单元写作2021-10-269页
- 八年级上数学课件八年级上册数学课2021-10-2620页
- (福建专版)2019春八年级物理下册第112021-10-269页
- 2019八年级物理下册 6物质的密度2021-10-264页
- 八年级数学上册期末复习专题巩固复2021-10-2618页