重庆市巴蜀中学初中部数学教研组整理：八年级数学上（RJ）12 25页

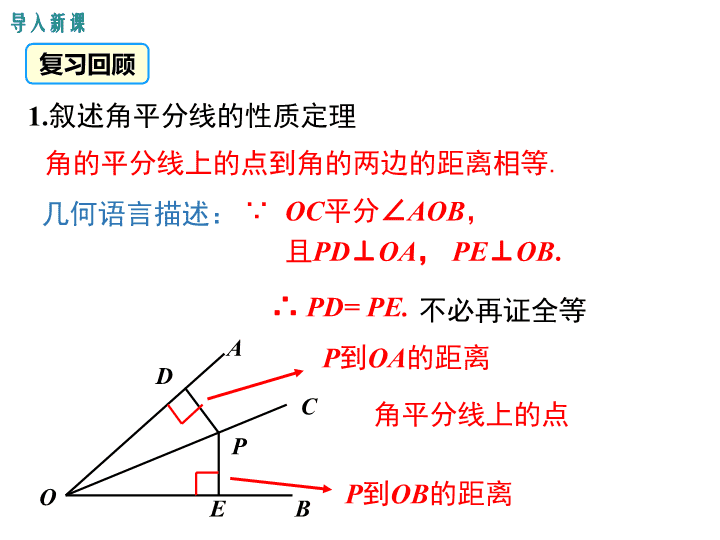
12.3 角的平分线的性质 第十二章 全等三角形 导入新课 讲授新课 当堂练习 课堂小结 第 2 课时 角平分线的判定 八年级数学上（RJ） 学习目标 1. 理解角平分线判定定理 .( 难点） 2. 掌握角平分线判定定理内容的证明方法并应用其解题 . （重点） 3. 学会判断一个点是否在一个角的平分线上 . 导入新课 复习回顾 O D P P 到 OA 的距离 P 到 OB 的距离 角平分线上的点 几何语言描述： ∵ OC 平分 ∠ AOB ， 且 PD ⊥ OA ， PE ⊥ OB . ∴ PD= PE. A C B 角的平分线上的点到角的两边的距离相等 . 1. 叙述 角平分线的性质定理 不必再证全等 E 2. 我们知道，角平分线上的点到角的两边的距离相等 . 那么到角的两边的距离相等的点是否在角的平分线上呢？ 到角的两边的距离相等的点在角的平分线上 . 讲授新课 角平分线的判定 一 P A O B C D E 角的内部到角的两边距离相等的点在角的平分线上． 问题： 交换角的平分线的性质中的已知和结论，你能得到什么结论，这个新结论正确吗？ 角平分线的性质： 角的平分线上的点到角的两边的距离相等 . ∵ OC 平分∠ AOB ， 且 PD⊥OA ， PE⊥OB ∴ PD= PE 几何语言： 猜想 : 思考：这个结论正确吗？ 已知：如图， PD ⊥ OA ， PE ⊥ OB ， 垂足分别是 D 、 E ， PD=PE . 求证：点 P 在 ∠ AOB 的角平分线上 . 证明： 作射线 OP ， ∴ 点 P 在 ∠ AOB 角的平分线上 . 在 Rt△ PDO 和 Rt△ PEO 中， （全等三角形的对应角相等） . OP=OP （公共边）， PD= PE （已知 ）， B A D O P E ∵ PD ⊥ OA , PE ⊥ OB. ∴∠ PDO =∠ PEO =90 °， ∴Rt△ PDO ≌ Rt△ PEO （ HL ） . ∴ ∠ AOP =∠ BOP 证明猜想 判定定理： 角的内部到角的两边的距离相等的点在角的平分线上 . P A O B C D E 应用所具备的条件： （ 1 ） 位置关系： 点在角的内部 ； （ 2 ） 数量关系： 该点到角两边的距离相等 . 定理的作用： 判断点是否在角平分线上 . 应用格式： ∵ PD ⊥ OA,PE ⊥ OB ， PD=PE. ∴ 点 P 在 ∠ AOB 的平分线上 . 知识总结 典例精析 例 1 ： 如图，要在 S 区建一个贸易市场，使它到铁路和公路距离相等， 离公路与铁路交叉处 500 米，这个集贸市场应建在何处（比例尺为 1︰20000 ） ？ D C S 解：作夹角的角平分线 OC ， 截取 OD =2.5cm , D 即为所求 . O 方法点拨： 根据角平分线的判定定理，要求作的点到两边的距离相等，一般需作这两边直线形成的角的平分线，再在这条角平分线上根据要求取点 . 活动 1 分别画出下列三角形三个内角的平分线 ，你发现了什么？ 三角形的内角平分线 二 发现：三角形的三条角平分线相交于一点 活动 2 分别 过交点作三角形三边的垂线，用刻度尺量一量，每组垂线段，你发现了什么？ 发现：过交点作三角形三边的垂线段相等 你能证明这个结论吗？ 已知：如图， △ ABC 的角平分线 BM ， CN 相交于点 P ， 求证：点 P 到三边 AB ， BC ， CA 的距离相等 . 证明结论 证明：过点 P 作 PD ， PE ， PF 分别垂直于 AB ， BC ， CA ，垂足分别为 D ， E ， F . ∵ BM 是△ ABC 的角平分线， 点 P 在 BM 上， ∴ PD=PE . 同理 PE=PF . ∴ PD=PE=PF . 即点 P 到三边 AB ， BC ， CA 的距离相等 . D E F A B C P N M 想一想： 点 P 在 ∠ A 的平分线上吗？这说明三角形的三条角平分线有什么关系？ 点 P 在 ∠ A 的平分线上 . 结论： 三角形的三条角平分线交于一点，并且这点到三边的距离相等 . D E F A B C P N M M E N A B C P O D 变式 1 ： 如图，在直角△ABC中，∠C＝90 ° ，AP平分∠BAC，BD平分∠ABC;AP,BD交于点O，过点O作OM⊥AC,若OM＝4, (1)求点O到△ABC三边的距离和. 温馨提示： 不存在垂线段———构造应用 12 解：连接OC M E N A B C P O D 变式 1 ： 如图，在直角△ABC中，∠C＝90 0 ，AP平分∠BAC，BD平分∠ABC;AP,BD交于点O，过点O作OM⊥AC,若OM＝4 . (2)若△ABC的 周长 为32，求△ABC的 面积 . 1. 应用角平分线性质： 存在 角平分线 涉及 距离问题 2 . 联系角平分线性质： 距离 面积 周长 条件 知识与方法 例 2 如图， 在△ABC中，点O是△ABC内一点，且点O到△ABC三边的距离相等．若∠A＝40°，则∠BOC的度数为(　　) A．110° B．120° C．130° D．140° A 解析： 由已知， O 到三角形三边的距离 相等，所以O是内心，即三条角平分线 的交点，AO，BO，CO都是角平分线， 所以有∠CBO＝∠ABO＝ ∠ABC， ∠BCO＝∠ACO＝ ∠ACB， ∠ABC＋∠ACB＝180°－40°＝140°， ∠OBC＋∠OCB＝70°， ∠BOC＝180°－70°＝110°. 由已知， O 到三角形三边的距离相等，得O是内心，再利用三角形内角和定理即可求出∠BOC的度数． 方法总结 归纳总结 角的平分线的 性质 图形 已知 条件 结论 P C P C OP 平分∠ AOB PD⊥OA 于 D PE⊥OB 于 E PD=PE OP 平分∠ AOB PD=PE PD⊥OA 于 D PE⊥OB 于 E 角的平分线的 判定 当堂练习 1. 如图，某个居民小区 C 附近有三条两两相交的道路 MN 、 OA 、 OB ， 拟在 MN 上建造一个大型超市，使得它到 OA 、 OB 的距离相等，请确定该超市的位置 P . 小区 C P A O B M N 2. 如图所示，已知 △ ABC 中， PE∥AB 交 BC 于点 E ， PF∥AC 交 BC 于点 F ， 点 P 是 AD 上一点，且 点 D 到 PE 的距离与到 PF 的距离相等，判断 AD 是否平分 ∠ BAC ，并说明理由． 解： AD 平分 ∠ BAC ． 理由如下： ∵ D 到 PE 的距离与到 PF 的距离相等， ∴点 D 在 ∠ EPF 的平分线上． ∴∠ 1 ＝∠ 2 ． 又 ∵ PE∥AB ，∴∠ 1 ＝∠ 3 ． 同理， ∠ 2 ＝∠ 4 ． ∴∠ 3 ＝∠ 4 ，∴ AD 平分 ∠ BAC ． A B C E F D ( ( ( ( 3 4 1 2 P 3. 已知：如图，OD平分∠POQ，在OP、OQ边上取OA＝OB，点C在OD上，CM⊥AD于M，CN⊥BD于N.求证：CM＝CN. 证明：∵OD平分线∠POQ， ∴∠AOD=∠BOD. 在△AOD与△BOD中， ∵OA=OB，∠AOD=∠BOD，OD=OD， ∴△AOD ≌ △BOD. ∴∠ADO=∠BD O . ∵CM⊥AD，CN⊥BD， ∴CM=CN. 4. 如图，已知∠ CBD 和 ∠ BCE 的平分线相交于点 F ， 求证：点 F 在∠ DAE 的平分线上． 证明： 过点 F 作 FG ⊥ AE 于 G ， FH ⊥ AD 于 H ， FM ⊥ BC 于 M . ∵点 F 在 ∠ BCE 的平分线上， 　　　　 FG ⊥ AE ， FM ⊥ BC. ∴ FG ＝ FM . 又∵点 F 在∠ CBD 的平分线上， 　　　　 FH ⊥ AD ， FM ⊥ BC ， ∴ FM ＝ FH ， ∴ FG ＝ FH . ∴点 F 在 ∠ DAE 的平分线上 . 　　　 G H M A B C F E D 拓展思维 5. 如图 , 直线 l 1 、 l 2 、 l 3 表示三条互相交叉的公路 , 现要建一个货物中转站 , 要求它到三条公路的距离相等 , 可选择的地址有几处 ? 画出它的位置 . P 1 P 2 P 3 P 4 l 1 l 2 l 3 课堂小结 角平分线 的判定定理 内容 角的内部到角两边距离相等的点在这个角的平分线上 作用 判断一个点是否在角的平分线上 结论 三角形的角平分线相交 于 内部一点