八年级数学下册第2章四边形2-4三角形的中位线课件（湘教版） 14页

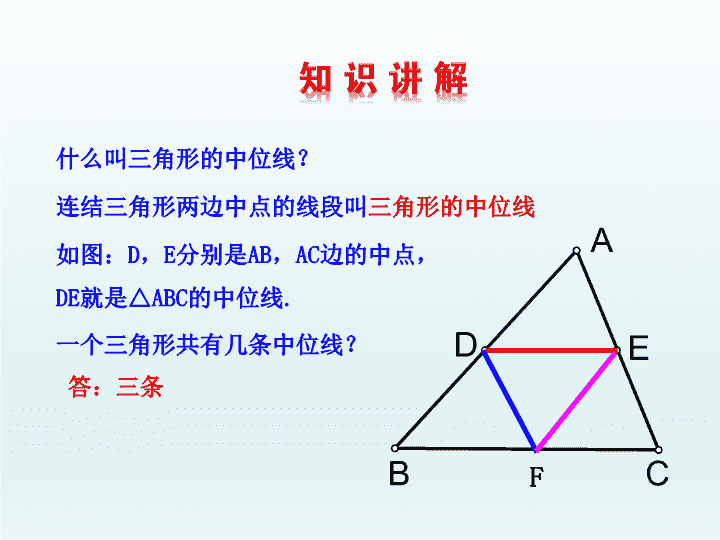
2.4 三角形的中位线 1. 了解三角形中位线的概念 . 2. 探索三角形中位线的性质，通过探索活动培养学生细心操作、大胆猜想、严格推理的好习惯 . 3. 会利用三角形中位线性质解决实际问题 . 什么叫三角形的中位线？ 连结三角形两边中点的线段叫 三角形的中位线 如图： D ， E 分别是 AB ， AC 边的中点， DE 就是△ ABC 的中位线 . 一个三角形共有几条中位线？ F 答：三条 三角形的中位线与三角形的中线有什么区别？ 中位线是 两个中点 的连线，而中线是 一个顶点 和对边 中点 的连线 . 三角形中位线有什么特殊性质吗？ 提示： 分别从位置上和数量上进行探究 . 猜想： 三角形的中位线平行且等于第三边的一半 . 三角形的中位线定理： 三角形的中位线平行于第三边，并且等于第三边的一半 . 应用格式： 因为在△ ABC 中， D ， E 分别是 AB ， AC 边的中点 . 所以 DE∥BC ， DE ＝ BC 例 已知如图：在△ ABC 中， AB ， BC ， CA 的中点分别是 E ， F ， G ， AD 是高 . 求 证： EF ＝ DG. 证明： EF 是△ ABC 的中位线 DG 是 Rt△ADC 斜边上的中线 所以 EF ＝ DG 你还想到了什么？ 【 例题 】 如图，已知△ ABM 和△ CAN 都是等边三角形， P ， Q ， R 分别是 BC ， BM ， CN 的中点，试说明 PQ=PR. 【 证明 】 连结 MC 、 BN, 由等边三角形 ABM 和等边三角形 CAN 知 AM=AB,AC=AN,∠MAC=∠BAN=60°+∠BAC, 所以△ MAC≌△BAN, 因此 MC=BN. 又 P 、 Q 、 R 分别是 BC 、 BM 、 CN 的中点 , 所以 PQ 、 PR 分别为△ BMC 和△ BNC 的中位线 , 因此 PQ= MC,PR= BN ，所以 PQ=PR. 【 跟踪训练 】 【 解析 】 2. 四边形的两条对角线长分别是 12 cm 和 10 cm ，顺次连结各边中点所得四边形的周长是（ ） （ A ） 10 cm （ B ） 18 cm （ C ） 22 cm （ D ） 12 cm 【 解析 】 选 C. 如图所示 ,AC=12 cm,BD=10 cm, E 、 F 、 G 、 H 为四边形 ABCD 各边中点， 则 EH=FG= BD=5 cm, HG=EF= AC=6 cm, 所以四边形 EFGH 的周长为 22 cm. 3. 如图，△ ABC 中，点 D ， E ， F 分别是边 AB ， BC ， AC 的中点，则△ DEF 与△ ABC 的面积之比为（ ） （ A ） 1∶4 （ B ） 1∶3 （ C ） 1∶2 （ D ） 1∶ 【 解析 】 选 A. 因为 DE 、 DF 是△ ABC 的中位线， 所以 DE∥CF ， DF∥CE ， 所以四边形 DFCE 是平行四边形， 所以△ DEF≌△CFE. 同理可证，△ AFD≌△EDF,△DEB≌△EDF, 所以 S △DEF = S △ABC . 【 解析 】 答案： 通过本课时的学习，需要我们 1. 理解三角形中位线的概念，了解三角形中线与三角形中位线的区别 . 2. 掌握三角形中位线的性质 . 3. 能利用三角形中位线的性质解决相关问题 无知识的人，其生命如同无叶子的树，缺少勃勃生机 .