八年级上数学课件八年级上册数学课件《轴对称》 人教新课标 (3)_人教新课标 43页

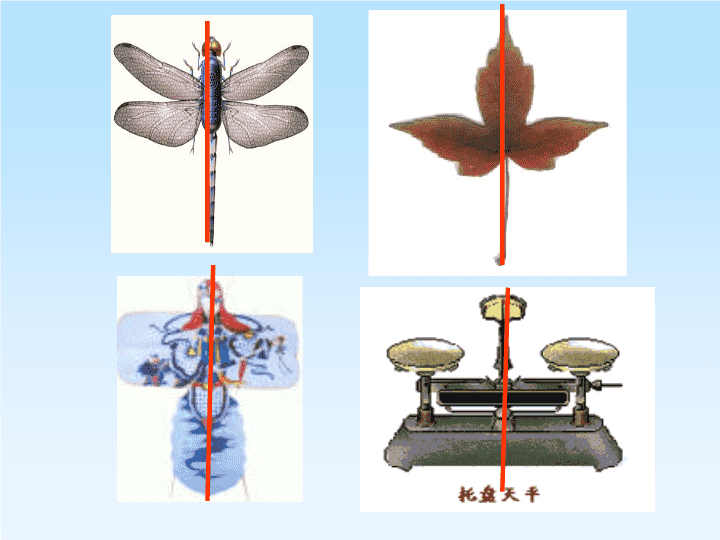
如果一个图形沿一条直线折叠后，直线 两旁的部分能够互相重合， 那么这个图形叫 做轴对称图形，这条直线叫做对称轴。 对称轴 下面的图形都是轴对称图形，请分别找出 每个图形的对称轴。 取一张纸，先对折，然后打开放在 桌上，在纸的一侧上滴一滴墨水，将纸 迅速合上、压平，再将纸打开，观察所 得到的图案。 位于折痕两侧的墨迹图案彼此之间 有什么关系？ 观察下图中的每组图案，你发现了什么？ 如果两个图形沿一条直线对折，它们能 完全重合，那么这两个图形成轴对称，这条 直线就是对称轴。 轴对称图形和轴对称是不是一回事?它们 有区别吗? 不同点：轴对称图形对一个图形而言。 成轴对称是对两个图形而言。 联系： 轴对称图形 成轴对称 请观察下面几何图形，哪些是轴对 称图形？并找出它们的对称轴。 等边三角形 一般三角形 一般等腰三角形 圆 等腰梯形 一般梯形 平行四边形 找出下列图形的对称轴 美国 加拿大 乌拉圭澳大利亚 国旗是一个国家的象征，观察下面的国旗 哪些是轴对称图形？找出它们的对称轴。 瑞典 英国 以色列 挪威 √ √√√ √ √ √ √ 找规律填空： 下列16个英文字母中，是轴对称图形的是 　　　 　　　 A　B　C　D　E　F　G　H　 　　 M　N　O　P　Q　R　S　T　 A B C D E H M O T 朴素的对称观念在我们的生活中广泛存在： ①文学中的对仗也是一种“对称”。王维的诗 句“明月松间照，清泉石上流”无非是把第一 句中的“明月”变成了第二句中的“清泉”， “松间”变成了“石上”，“照”变成了 “流”，词意变了，但是词性和句式结构并没 有变.由于工整的文字对仗,使王维诗的自然意 境之美得到很好地表现.我国文学中的歌赋尤 其是对联，更把“对称”的要求推进到极高的 境界. 阅读讨论 对称与文化 ②我国人民喜闻乐见的京剧脸谱，多是对称的 图形，民族建筑中整体或局部呈对称的现象更 是常见. ③对称概念在物理学等领域中也起着重要的作用. 著名的物理学家杨振宇和李政道获得的诺贝尔奖 研究成果——“宇称不守恒”就和对称密切相关.杨 振宇在《对称和物理学》一文中写道：“在理解 物理世界的过程中,21世纪会目睹对称概念的新方 面吗？我的回答是，十分可能” 。 正如20世纪著名数学家赫尔曼.外尔所说 的，“对称是一种思想，通过它，人们毕生追 求，并创造次序、美丽和完善……”对称的涵 义已远远超出了数学的范畴，它出现在自然、 艺术、科学、建筑乃至诗歌 中。对称是一种美， 生活有了“对称” 会更美。 华岩教育课程辅导中心（济源） 常年招收初中各年级一对一、一对多、小班学生 招生学科：英语、数学、物理、化学、地理、生物 学习环境： 1、夏季空调、冬季市政供暖全天候开放 2、免费矿泉水全天候供应 您还可以免费享受到我们以下周到的服务： 1、免费试听三次（三次课以内无论任何理由离开我处，均不需要交 纳任何费用） 2、免费提供相关学习资料 3、免费咨询学习、心理等各方面信息 4、免费不定期开设家长课程，讲授中学生心理和家庭教育相关知识 上课地点：河南省济源市世纪广场南侧华新东区（华新花园） 详情咨询：18603892560 联 系 人：梁老师 A B C A′ C′ B′ 如图，△ABC和 △A'B'C' 关于直线MN对称，点A、 B、C分别是点A',B',C'的 对称点，线段AA'、BB'、 CC'与MN有什么关系？ P 　点A，A′是对称点，设 AA′交对称轴MN于点P， 将△ABC和 △A′B′C′沿直 线MN折叠后，点Ａ与Ａ′ 重合，于是有： ＡＰ＝ＰＡ′，∠ＭＰＡ＝ ∠ＭＰＡ′＝９0° 对称轴所在的直线经过对称点所连线段的中 点，并且垂直于这条线段。 A B C A′ C′ B′ P. . Q 定义： 经过线段的中点并且垂直于 这条线段的直线，就叫这条线段 的垂直平分线，也叫中垂线。 A B C A' C′ B′ 几何语言： ∵MN是AA′的垂直平分线 ∴AP=PA′, ∠MPA= ∠MPA′=90° C A'A B B' C' l l垂直平分 AA' l垂直平分BB' l垂直平分CC' A B l P1 P2 P3 P4 如图，木条l与AB钉在一起，l 垂直平分AB， P1 ，P2, P3 P4,…是l上的点，分别量出点 P1 ，P2, P3 P4 ，…到A与B的 距离，你有什么发现？ 发现： AP1=BP1;AP2=BP2; AP3=BP3;AP4=BP4. A BC P l 直线l⊥AB，垂足是C，AC=CB, 点P在l上，求证PA=PB. 证明：∵ l⊥AB， ∴∠PCA=∠PCB=90° 又∵ AC=CB，PC=PC, ∴△PCA ≌ △ PCB(SAS) ∴PA=PB 　　线段平分线上的点与这 条线段两个端点的距离相等。 线段垂直平分线的性质： Ｐ Ａ l Ｃ Ｂ 几何语言： ∵ l ⊥ＡＢ ∴ＰＡ＝ＰＢ 　　与一条线段两个端点距 离相等的点，在这条线段的 垂直平分线上。 线段垂直平分线的判定： Ｐ Ａ l Ｃ Ｂ 几何语言： ∵ PA＝PB ∴ l 是AB的垂直平分线 A B M N D D CB E A 解： 1.垂直平分线的定义： ∵MN是AB的垂直平分线 ∴ ， ； 2.垂直平分线的性质： ∵MN是AB的垂直平分线 ∴ （ ） 3.垂直平分线的判定： ∵PA＝PB ∴ （ ） MN⊥AB P A B M N D AD＝BD PA＝PB P在AB的垂直平分线上 例1：如图，点A与点B关于某条直线成轴对称， 你能作出这条直线吗？ A B 分析：我们只要连接点A和点B，画 出线段AB的垂直平分线，就可以得 到点A和点B的对称轴. 而由两点确 定一条直线和线段垂直平分线的性 质，只要作出到点A、B距离相等的 两点即可. 作法： 1.分别以点A、B为圆心，以大于1/2AB的 长为半径作弧，两弧交于C、D两点； 2.作直线CD. C D ∴直线CD即为所求 例2：如图是一颗五角星，你能作出它的所有对称 轴吗？ 作法： 1.找出它的一对对称点（例如A和A’）； 2.作线段AA’的垂直平分线 l. A A’ l用类似的的方法，就可 以作出其他四条对称轴. 你也试一试！ 练习1：作出下列图形的一条对称轴，和同学比较 一下，你们作出的对称轴一样吗？ 练习2：如图，角是轴对称图形吗？如果是，它的 对称轴是什么？角是轴对称图形，角平分线所在 的直线就是角的对称轴. 练习3：如图，与图形A成轴对称的是哪个图形？ 画出它们的对称轴. 练习4：如图，在Rt△ABC 中，∠C＝90°，AD是角平 分线且AD＝BD，AC＝10. 求AB的长度. 提示：过点D作 DE⊥AB于E A B CD E