八年级上数学课件八年级上册数学课件《探索勾股定理》 北师大版 (1)_北师大版 19页

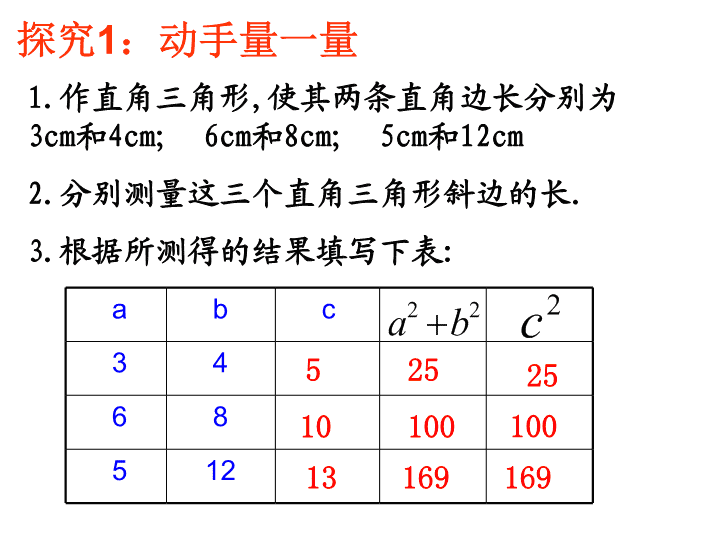
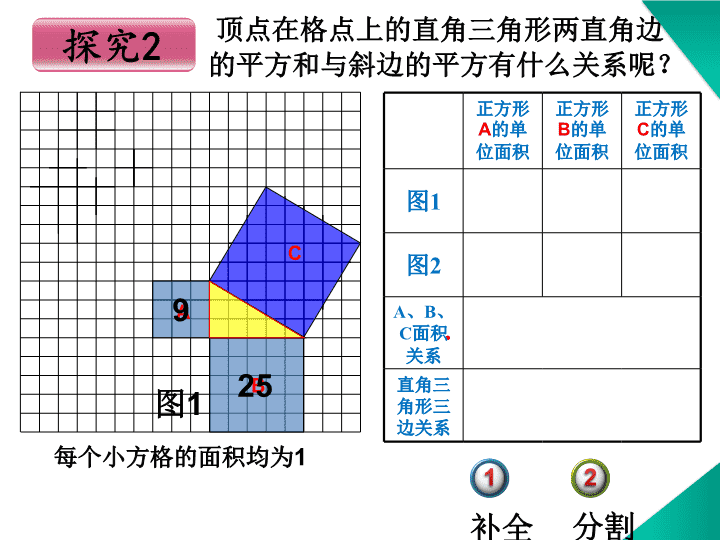
探索勾股定理 探究1：动手量一量 1.作直角三角形,使其两条直角边长分别为 3cm和4cm; 6cm和8cm; 5cm和12cm 2.分别测量这三个直角三角形斜边的长. 3.根据所测得的结果填写下表: a b c 3 4 6 8 5 12 22 ba  2c 5 25 25 10 100 100 13 169169 顶点在格点上的直角三角形两直角边 的平方和与斜边的平方有什么关系呢？ 每个小方格的面积均为1 A B C 图1 正方形A 的单位 面积 正方形B 的单位 面积 正方形C 的单位 面积 图1 图2 A、B、 C面积 关系 直角三 角形三 边关系 9 25 分割补全 探究2 正方形A 的单位 面积 正方形B 的单位 面积 正方形C 的单位 面积 图1 图2 A、B、 C面积 关系 直角三 角形三 边关系 探究2 每个小方格的面积均为1 A B C 图2 9 25 分割补全 34 A B C 图1 4 9 13 CBA SSS  a²+b²=c² 顶点在格点上的直角三角形两直角边 的平方和与斜边的平方有什么关系吗？ 猜想： 如果a、b为直角三角形的两条直角 边长，c为斜边长，那么 2 2 2a b c  a b c 即直角三角形两直角边的平方和 等于斜边的平方。 C B A ☞ 拼图游戏: 给定四个全等的直角三角形纸片,假设三角 形的两直角边分别为a、b，斜边为c。你们能用 这四个三角形纸片，围出一个正方形吗? 你能用所拼图形的面积关系来验证所得猜想吗？ a b c c b 2c面积 2a-b)面积 （ ab 2 14面积 4S S S小正方形 个三角形 大正方形＋ 2 21(a -b ) + 4 a b c 2   即a2+b2=c2 a b c4个 a-b a-b 你能用所拼图形的面积关系来验证所得猜想吗? 即a2+b2=c2 c c a b c4个 2b)a （面积 2c面积 ab 2 14面积 22 cab 2 14-b)a （ 小正方形个三角形大正方形 SSS  4 b b ca b 你能用所拼图形的面积关系来验证所得猜想吗? 勾股定理 　　如果直角三角形两直角边分别为a、b， 斜边为c，那么 2 2 2a b c  　　即 直角三角形两直角边的平方和等于 斜边的平方． a b c 在西方又称毕达哥拉 斯定理！ 中国古代数学家——赵爽的验证方法 a bc ab  A B C D 2c正方形ABCD的面积为 还可以认为是四个三角 形与一个小正方形的和，即 22 )(4) 2 1( ababc ∴ 2)(4) 2 1( abab  ∴ 222 cba  2002年在北京召开的国际数学 家大会的会标就是依据我国古 代数学家赵爽的弦图制作的。 ∴ ∵ 数 学 故 事 链 接 相 传 两 千 五 百 年 前 ， 一 次 毕 达 哥 拉 斯 去 朋 友 家 作 客 ， 发 现 朋 友 家 用 砖 铺 成 的 地 面 反 映 直 角 三 角 形 三 边 的 某 种 数 量 关 系 ， 同 学 们 ， 我 们 也 来 观 察 下 面 图 案 ， 看 你 能 发 现 什 么 ？ 　　数学家毕达哥拉斯的发现： A、B、C的面积有什么关系？ SA+SB=SC A B C 商高是公元前十一世纪(西周)的 中国人。在大约战国时期西汉 的数学著作 《周髀 算经》中记 录着商高同周公的一段对话。 商高说：“…故折矩，勾广三， 股修四，经隅五。” 后来人们 就简单地把这个事实说成“勾 三股四弦五”。这就是著名的 勾股定理. 短直角边 （勾） 长直角边 （股） 斜边 （弦） 3 4 5 5 12 13 6 8 10 7 24 25 短直角边 （勾） 长直角边 （股） 斜边 （弦） 8 15 17 9 12 15 9 40 41 10 24 26 勾 股 弦 勾三 股 四 弦 五 2 2 12 2 1 cab  2)( 2 1 ba   222 cba  练一练： 1.勾股定理的内容 2.勾股定理的证明方法 4.探究—猜想—归纳—推理的数学思想 你说我说 大家说 请你谈谈通过本节课的 学习你学到了什么! 3.数形结合思想