人教版初中数学八年级下册课件18.1.2 平行四边形判定第3课时 三角形的中位线 32页

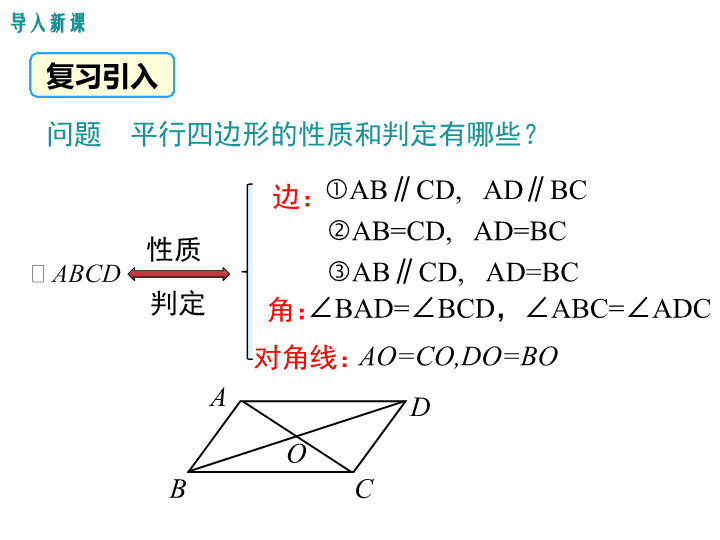
18.1.2 平行四边形判定 第十八章 平行四边形 导入新课 讲授新课 当堂练习 课堂小结 第3课时 三角形的中位线 学习目标 1.理解三角形中位线的概念，掌握三角形的中位线 定理.（重点） 2.能利用三角形的中位线定理解决有关证明和计算 问题.(重点） 问题 平行四边形的性质和判定有哪些？ 导入新课 复习引入 ABCD 边： 角： 对角线： B O DA C AB∥CD, AD∥BC AB=CD, AD=BC AB∥CD, AD=BC ∠BAD=∠BCD，∠ABC=∠ADC AO=CO,DO=BO 判定 性质 我们探索平行四边形时，常常转化为三角形，利 用三角形的全等性质进行研究，今天我们一起来 利用平行四边形来探索三角形的某些问题吧. 思考 如图，有一块三角形蛋糕，准备平分给四个小朋 友，要求四人所分的形状大小相同，该怎样分呢？ 讲授新课 三角形的中位线定理一 概念学习 定义：连接三角形两边中点的线段叫做三角形的中位线. 如图，在△ABC中，D、E分别是AB、AC的中点，连 接DE.则线段DE就称为△ABC的中位线. 问题1 一个三角形有几条中位线？你能在△ABC 中画出它所有的中位线吗？ D E  F 有三条，如图，△ABC的 中位线是DE、DF、EF. 问题2 三角形的中位线与中线有什么区别？ 中位线是连接三角形两边中点的线段. 中线是连结一个顶点和它的对边中点的线段. 问题3：如图，DE是△ABC的中位线， DE与BC有怎样的关系？ D E 两条线段的关系 位置关系 数量关系 分析： DE与BC的关系猜想 DE∥BC ？ 1 2 DE BC 度量一下你手中的三角形，看看是否有同 样的结论？并用文字表述这一结论． 问题4： 平行 角 平行四边形或 线段相等 一条线段是另一条线段的一 半 倍长短线 分析1： D E 猜想： 三角形的中位线平行于三角形的 第三边且等于第三边的一半． 问题3：如何证明你的猜想？ 分析2： D E 互相平分 构 造 平行四边形倍长DE 证明： D E 延长DE到F，使EF=DE． 连接AF、CF、DC ． ∵AE=EC，DE=EF ， ∴四边形ADCF是平行四边形． F ∴四边形BCFD是平行四边形， ∴CF AD ,/ / ∴CF BD ,/ / 1 2 DE DF又∵ ， ∴DF BC ．/ / ∴ DE∥BC， ．1 2 DE BC 证一证 1 . 2 DE BC DE BC∥ ， D E证明：延长DE到F，使EF=DE． F ∴四边形BCFD是平行四边形． ∴△ADE≌ △CFE． ∴∠ADE=∠F 连接FC． ∵∠AED=∠CEF，AE=CE， 证法2： ，AD=CF, ∴BD CF．/ / 1 2 DE DF又∵ ， ∴DF BC ．/ / ∴ DE∥BC， ．1 2 DE BC ∴CF AD ,/ / 三角形的中位线平行于三角形的第三边且等于第三 边的一半． D E △ABC中，若D、E分别是边AB、AC的中点， 则DE∥BC，DE= BC． 1 2 三角形中位线定理： 符号语言： 归纳总结 D E  F 重要发现： ①中位线DE、EF、DF把 △ABC 分成四个全等的三角形；有三 组共边的平行四边形，它们是 四边形ADFE和BDEF，四边形 BFED和CFDE，四边形ADFE 和DFCE.②顶点是中点的三角形，我们称之为中点三角形； 中点三角形的周长是原三角形的周长的一半.面积等 于原三角形面积的四分之一. 由此你知道怎 样分蛋糕了吗 典例精析 例1 如图，在△ABC中，D、E分别为AC、BC的中 点，AF平分∠CAB，交DE于点F.若DF＝3，求AC的 长解：∵D、E分别为AC、BC的中点， ∴DE∥AB， ∴∠2＝∠3. 又∵AF平分∠CAB， ∴∠1＝∠3， ∴∠1＝∠2， ∴AD＝DF＝3， ∴AC＝2AD＝2DF＝6. 1 2 3 例2 如图，在四边形ABCD中，AB=CD，M、N、P 分别是AD、BC、BD的中点，∠ABD=20°， ∠BDC=70°，求∠PMN的度数． 解：∵M、N、P分别是AD、BC、BD的中点， ∴PN，PM分别是△CDB与△DAB的中位线， ∴PM= AB，PN= DC，PM∥AB，PN∥DC， ∵AB=CD， ∴PM=PN， ∴△PMN是等腰三角形， ∵PM∥AB，PN∥DC， ∴∠MPD=∠ABD=20°，∠BPN=∠BDC=70°， ∴∠MPN=∠MPD+(180°−∠NPB)=130°， ∴∠PMN=(180°−130°)÷ 2 =25°． 1 2 1 2 例3 如图，在△ABC中，AB＝AC，E为AB的 中点，在AB的延长线上取一点D，使BD＝AB， 求证：CD＝2CE. 证明：取AC的中点F，连接BF. ∵BD＝AB， ∴BF为△ADC的中位线，∴DC＝2BF. ∵E为AB的中点，AB＝AC， ∴BE＝CF，∠ABC＝∠ACB. ∵BC＝CB，∴△EBC≌ △FCB, ∴CE＝BF， ∴CD＝2CE.  F 恰当地构造三角形中位线是解决线段倍分关系的 关键． 归纳 练一练 1. 如图，△ABC中，D、E分别是AB、AC中点． （1） 若DE=5，则BC= ． （2） 若∠B=65°，则∠ADE= °． （3） 若DE+BC=12，则BC= ． 10 65 8 2.如图，A，B两点被池塘隔开，在A，B外选一 点C，连接AC和BC，并分别找出AC和BC的中点 M，N，如果测得MN=20m，那么A，B两点间的 距离为______m． N M 40 例4 如图，在四边形ABCD中，E、F、G、H 分别是AB、BC、CD、DA中点． 求证：四边形EFGH是平行四边形． 四边形问题 连接对角线 三角形问题 （三角形中位线定理） 三角形的中位线的与平行四边形的综合运用二 分析： 证明:连接AC. ∵E,F,G,H分别为各边的中点, ∴ EF∥HG, EF=HG. ∴EF∥AC, HG∥AC, ∴四边形EFGH是平行四边形. 顺次连结四边形四条边的中点，所得的四 边形是平行四边形. 归纳 【变式题】如图，E、F、G、H分别为四边形 ABCD四边之中点．求证：四边形EFGH为平行四 边形.证明：如图，连接BD. ∵E、F、G、H分别为四边形 ABCD四边之中点， ∴EH是△ABD的中位线， FG是△BCD的中位线， ∴EH∥BD且EH= BD， FG∥BD且FG= BD， ∴EH∥FG且EH=FG， ∴四边形EFGH为平行四边形. 1 2 1 2 证明：∵D、E分别为AB、AC的中点， ∴DE为△ABC的中位线， ∴DE∥ BC，DE= BC. ∵CF= BC， ∴DE=FC； 1 2 1 2 例5 如图，等边△ABC的边长是2，D、E分别为 AB、AC的中点，延长BC至点F，使CF= BC， 连接CD和EF． （1）求证：DE=CF； 1 2 例5 如图，等边△ABC的边长是2，D、E分别 为AB、AC的中点，延长BC至点F，使CF= BC， 连接CD和EF． （2）求EF的长． 解：∵DE∥FC，DE=FC， ∴四边形DEFC是平行四边形， ∴DC=EF， ∵D为AB的中点，等边△ABC的边长是2， ∴AD=BD=1，CD⊥AB，BC=2， ∴EF=DC= ．3 1 2 练一练 1.如图，在△ABC中，AB=6，AC=10，点D，E，F 分别是AB，BC，AC的中点，则四边形ADEF的周 长为 （　 　） A.8 B.10 C.12 D.16 D 2.如图，▱ ABCD的周长为36，对角线AC，BD相交 于点O，点E是CD的中点，BD=12，求△DOE的周 长． 解：∵▱ ABCD的周长为36， ∴BC+CD=18． ∵点E是CD的中点， ∴OE是△BCD的中位线，DE= CD， ∴OE= BC， ∴△DOE的周长为OD+OE+DE= （BD+BC+CD）=15， 即△DOE的周长为15． 1 2 1 2 1 2 当堂练习 2.如图，在▱ ABCD中，AD=8，点E，F分别是 BD，CD的中点，则EF等于 （　　） A.2 B.3 C.4 D.5 1.如图，在△ABC中，点E、F分别为AB、AC的 中点．若EF的长为2，则BC的长为 （　　） A.1 B.2 C.4 D.8 第2题图第1题图 C C 3.如图，点 D、E、F 分别是 △ABC 的三边AB、BC、 AC的中点. （1）若∠ADF=50°，则∠B= °； （2）已知三边AB、BC、AC分别为12、10、8， 则△ DEF的周长为 . 50 15 A B C D F E 4.在△ABC中，E、F、G、H分别为AC、CD、 BD、 AB的中点，若AD=3，BC=8，则四边形EFGH的周 长是 . A B D C E F G H 11 5.如图，在△ABC中，AB=6cm，AC=10cm，AD 平分∠BAC，BD⊥AD于点D，BD的延长线交AC 于 点F，E为BC的中点，求DE的长． 解：∵AD平分∠BAC，BD⊥AD， ∴AB=AF=6，BD=DF， ∴CF=AC-AF=4， ∵BD=DF，E为BC的中点， ∴DE= CF=2． 1 2 6.如图，E为▱ ABCD中DC边的延长线上一点，且 CE＝DC，连接AE，分别交BC、BD于点F、G，连接 AC交BD于O，连接OF，判断AB与OF的位置关系和 大小关系，并证明你的结论． 解：AB∥OF，AB＝2OF. 证明如下：∵四边形ABCD是平行四边形， ∴AB＝CD，AB∥CD，OA＝OC， ∴∠BAF＝∠CEF，∠ABF＝∠ECF. ∵CE＝DC， ∴AB＝CE, ∴△ABF≌ △ECF(ASA)， ∴BF＝CF.∵OA＝OC， ∴OF是△ABC的中位线， ∴AB∥OF，AB＝2OF. 7.如图，在四边形ABCD中， AC⊥BD，BD=12，AC=16，E，F分 别为AB，CD的中点，求EF的长． 解：取BC边的中点G，连接EG、FG． ∵E，F分别为AB，CD的中点， ∴EG是△ABC的中位线，FG是△BCD的中位线， 又BD=12，AC=16，AC⊥BD， ∴EG=8，FG=6，EG⊥FG， ∴ ∴EG∥AC, FG∥BD, G 课堂小结 三角形的 中位线 三角形中位线平行 于第三边，并且等 于它的一半 三角形的中 位线定理 三角形的中位线 定理的应用