八年级下数学课件《反比例函数》 (5)_苏科版 19页

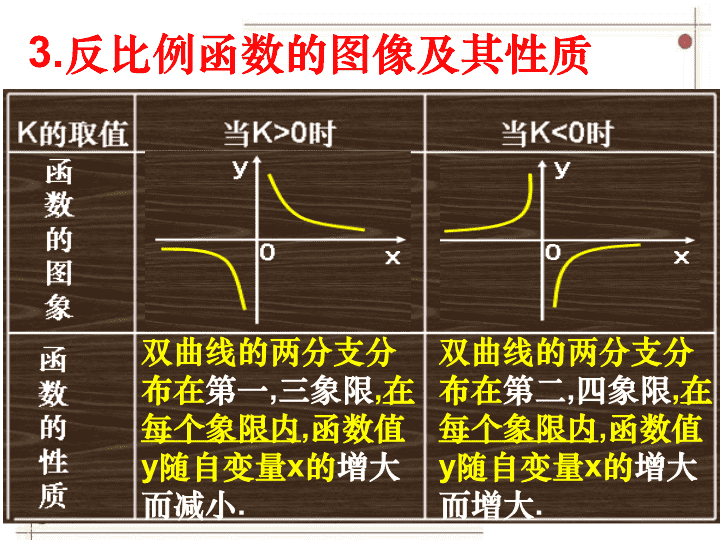
第11章 反比例函数 复习要点 1.反比例函数的定义: 函数 y= (k是常数,且k≠0)叫做反 比例函数. 2.反比例函数解析式的变形式: 1) y=kx-1 (k≠0) 2) xy=k (k≠0) k x 3.反比例函数的图像及其性质: 双曲线的两分支分 布在第一,三象限,在 每个象限内,函数值 y随自变量x的增大 而减小. 双曲线的两分支分 布在第二,四象限,在 每个象限内,函数值 y随自变量x的增大 而增大. 1.所受压力为F (F为常数且F≠ 0) 的物体， 所受压强P与所受面积S的图像大致为 （ ） P P P P S SS S O OO O （A） （B） （C） （D） B 热身练习 2.当x>0时反比例函数y=2/x的 图像在( ) A.第一象限 B.第二象限 C.第三象限 D.第四象限 A 3. 如图,点P是反比例函数图像上的 一点, 过点P分别向x轴、y轴作垂线, 若阴影部分面积为3,则这个反比例 函数是 .3y k  x y oM Np 4.如图,P是x轴上一动点,过点P作x轴的 垂线PQ交双曲线于点Q,连结OQ,当点P 沿x轴正半轴方向运动时,Rt△QOP的面 积( ) A.逐渐增大 B.逐渐减小 C.保持不变 D.无法确定 C 矩形的面积 三角形的面积 KS 2 1 KS  典型例题 例1 函数y=k/x与y=kx+k在同一 坐标系内的图像大致是( )B 例2.已知点A(-2,y1),B(-1,y2) 都在反比例函数 的图像 上,则y1与y2的大小关系(从大到小) 为 .  -4y xx ky  (k＜0) A(x1,y1),B(x2,y2)且x1＜0＜x2 y x o x 1 x2 A y1 y2 B y1 ＞0＞y2y2＞y1 利用特殊值法或图 像法。增减性要考 虑在每一象限内。 例3.正比例函数与反比例函数的图像交 于A，C两点,AB⊥ X轴于B，CD⊥ X轴 于 D，则四边形ABCD的面积___　2 巩固提高 1.函数y= 的图像过（2，-2）则 此函数的图像在平面直角坐标系中的 （ ） A.第一、三象限 B.第二、四象限 C.第一、二象限 D.第二、四象限 D k x 2.函数y= （k≠0）的图像如图所示， 那么函数y=kx-k 的图像大致是____ k x C 3.两位同学在描述同一反比例函数的图像时,甲同学 说:这个反比例函数图像上任意一点到两坐标轴的距 离的积都是3;乙同学说:这个反比例函数的图像与直 线y=x有两个交点,你认为这两位同学所描述的反比例 函数的解析式是 ( )A 4. 已知反比例函数y=k/x(k≠0)和一次函 数y=-x-6 (1)若一次函数和反比例函数的图像交于 点(-3,m),求m和k的值 . (2)当k值满足什么条件时,这两个函数的 图像有两个不同的交点? 解:(1)由两图像交于点(-3,m),得 3 6 3 m km     解得, 3 9 m k     ∴m,k的值分别为-3,9. 解： ( 0) 6 ky kx y x        解得, 6k xx    即,x2+6x+k=0 由题意：△=62-4k>0, 解得, k<9,且k≠0 (2)当k值满足什么条件时,这两个函 数的图像有两个不同的交点? 如图，直线y=k和双曲线 交于点 P，过P点作PA0⊥x轴于A0，x轴上的点A0， A1，A2，…，An的横坐标是连续的整数， 过点A0，A1，A2，…，An 分别作x轴的垂线， 与双曲线及直线y=k分别交于B1，B2，…，Bn； C1，C2，…，Cn。 P y xO A0 A1 A2 An C1 C2 Cn B1 B2 Bn … … … 1、求点AO的坐标 y=k 思考题 ky x  2、求 及 的值 11 11 BA BC 22 22 BA BC 3、试猜想 的值 nn nn BA BC P y xO A0 A1 A2 An C1 C2 Cn B1 B2 Bn … … y=k 通过这节课的学习， 你有什么收获？