8上导学案北师大版数学《第一章勾股定理》 9页

第一章 勾股定理 ‎1.1探索勾股定理 一、问题引入：‎ ‎（1）观察下面下图，若每个小正方形的面积为1，则 第①个图中，= ，= ，= .‎ 第②个图中，= ，= ，= .‎ 三个正方形A、B、C的面积之间有什么关系？以上结论与三角形三边有什么关系？ ‎ ‎ 通过这种关系你发现了什么？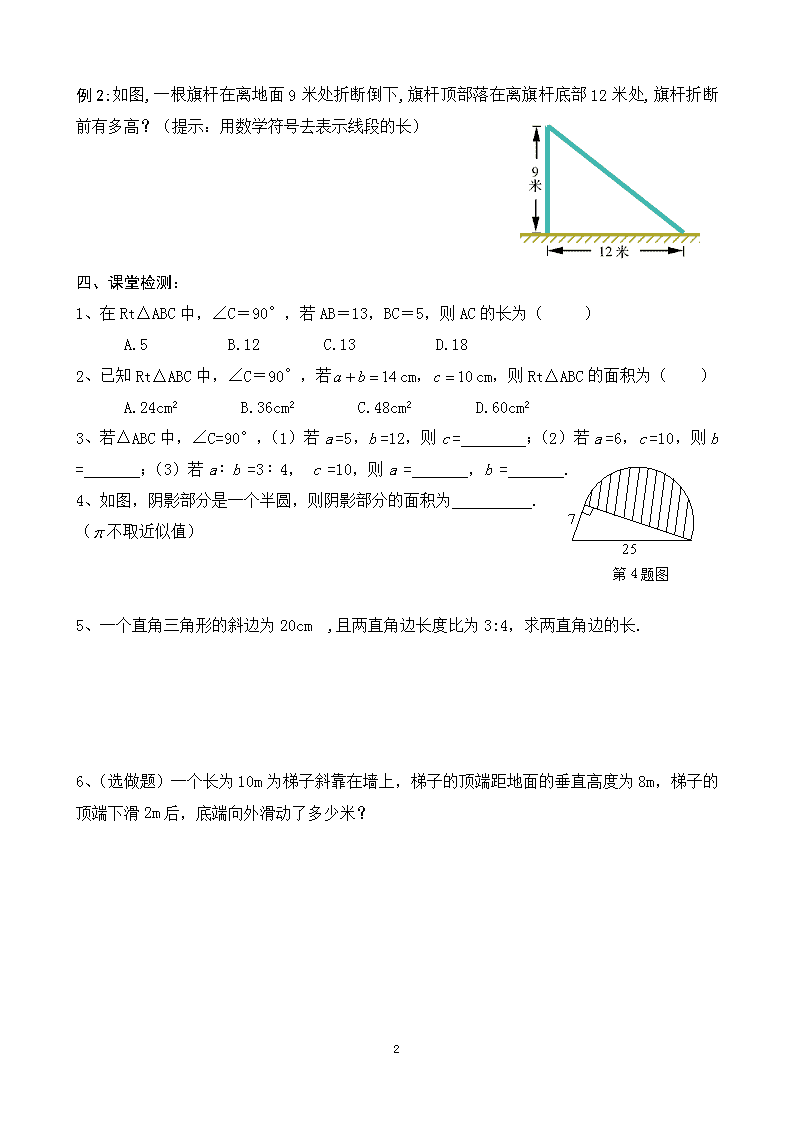 ‎ 勾股定理：如果直角三角形两直角边长分别为、，斜边长为，那么 ‎ ‎ 即直角三角形 的平方和等于 的平方.‎ 二、基础训练：‎ ‎1、如图（1），图中的数字代表正方形的面积，则正方形A的面积为　　　　 .‎ ‎ ‎ ‎ （1） （2）‎ ‎2、如图（2），三角形中未知边x与y的长度分别是x=　 　 　，y=　 　　 .‎ ‎3、在Rt△ABC中，∠C＝90°，若AC＝6，BC＝8，则AB的长为（ ）‎ A.6 B.8 C.10 D.12‎ 三、例题展示：‎ 例1:在△ABC中，∠C=90°，‎ ‎（1）若a=3，b=4，则c=_____________；‎ ‎（2）若a=9，c=15，则b=______________；‎ 9‎ 例2:如图,一根旗杆在离地面9米处折断倒下,旗杆顶部落在离旗杆底部12米处,旗杆折断前有多高？（提示：用数学符号去表示线段的长）‎ 四、课堂检测：‎ ‎1、在Rt△ABC中，∠C＝90°，若AB＝13，BC＝5，则AC的长为（ ）‎ A.5 B.12 C.13 D.18‎ ‎2、已知Rt△ABC中，∠C＝90°，若cm，cm，则Rt△ABC的面积为（　　）‎ A.24cm2　　　 B.36cm2　　　　C.48cm2　　　　D.60cm2‎ ‎3、若△ABC中，∠C=90°，（1）若a =5，b =12，则c = ；（2）若a =6，c =10，则b = ；（3）若a∶b =3∶4， c =10，则a = ，b = .‎ ‎4、如图，阴影部分是一个半圆，则阴影部分的面积为　　　　　.‎ ‎（不取近似值）‎ 第4题图 ‎5、一个直角三角形的斜边为20cm ,且两直角边长度比为3:4，求两直角边的长.‎ ‎6、（选做题）一个长为10m为梯子斜靠在墙上，梯子的顶端距地面的垂直高度为8m，梯子的顶端下滑2m后，底端向外滑动了多少米？‎ 9‎ 第一章 勾股定理 ‎1.2 一定是直角三角形吗 一、问题引入：‎ 1、 分别以下列每组数为三边作出三角形，用量角器量一量，它们都是直角三角形吗?‎ ‎(1)3, 4, 5 (2)6, 8, 10‎ ‎2、以上每组数的三边平方存在什么关系？结合上题你能得到什么结论？‎ ‎3、如果三角形的三边长a，b，c满足 ，那么这个三角形是直角三角形. ‎ ‎4、满足a2+b2=c2的三个 ，称为勾股数.‎ 二、基础训练：‎ ‎1、在下列长度的各组线段中，能组成直角三角形的是（ ）‎ A. 5，6，7 B. 1，4，9 C. 5，12，13 D. 5，11，12‎ ‎2、下列几组数中，为勾股数的是（ ）‎ A. 4，5，6 B. 12，16，20 C. 10，24，26 D. 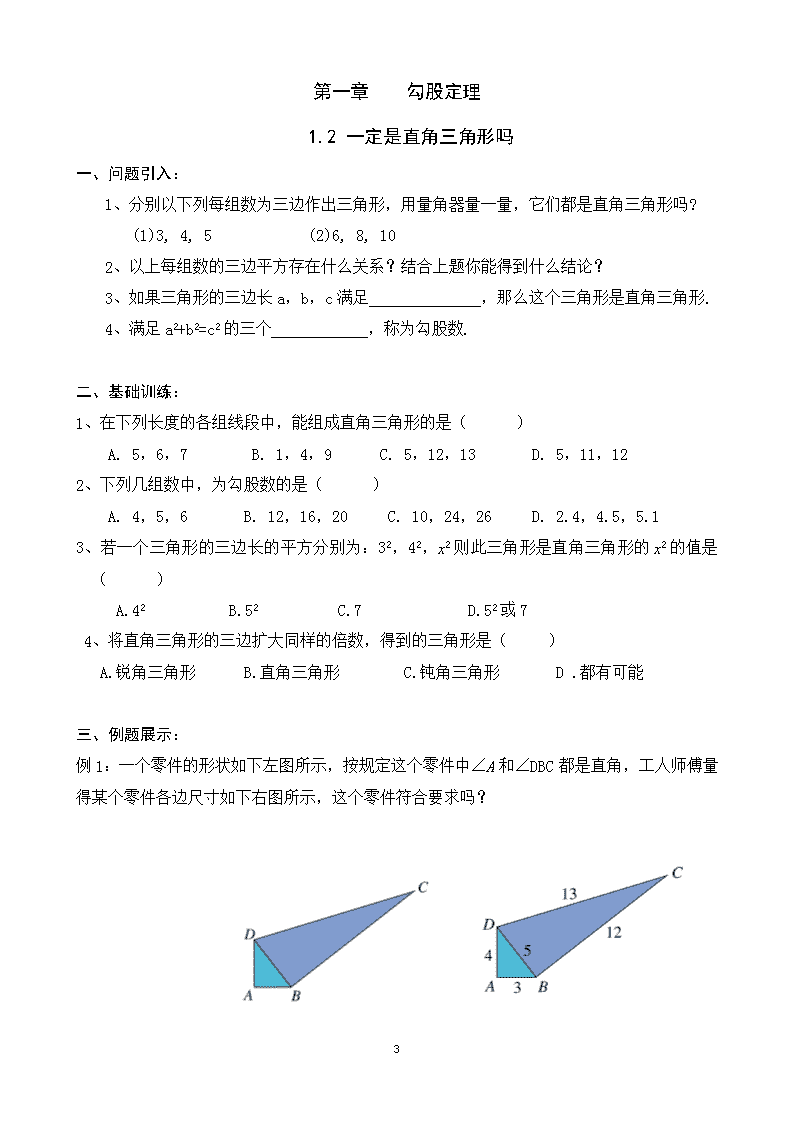2.4，4.5，5.1‎ ‎3、若一个三角形的三边长的平方分别为：32，42，x2则此三角形是直角三角形的x2的值是（ ）‎ A.42 B.52 C.7 D.52或7‎ ‎4、将直角三角形的三边扩大同样的倍数，得到的三角形是（ ）‎ ‎ A.锐角三角形 B.直角三角形 C.钝角三角形 D .都有可能 三、例题展示：‎ 例1：一个零件的形状如下左图所示，按规定这个零件中∠A和∠DBC都是直角，工人师傅量得某个零件各边尺寸如下右图所示，这个零件符合要求吗？‎ ‎ ‎ 9‎ 例2：如图，在正方形ABCD中，AB=4，AE=2，DF=1，图中有几个直角三角形？请说出你的判断理由.‎ 四、课堂检测：‎ ‎1、三角形的三边分别等于下列各组数，所代表的三角形是直角三角形的是（　　）‎ A. 7，8，10 B. 7，24，25 C. 12，35，37 D. 13，11，10‎ ‎2、若△ABC的三边a、b、c满足（a－b）（＋－）＝0，则△ABC是（　　　）‎ A.等腰三角形 B.直角三角形 C.等腰直角三角形 　 D.等腰三角形或直角三角形 ‎3、满足下列条件的△ABC，不是直角三角形的是（ ）‎ A. b2 =c2－a2 B. a∶b∶c=3∶4∶5‎ C.∠C =∠A+∠B 　　　 D.∠A∶∠B∶∠C =2∶3∶4‎ ‎4、若三角形的三边之比为3﹕4﹕5，则此三角形为 三角形.‎ ‎5、已知一个三角形的三边长分别是12cm，16cm，20cm，则这个三角形的面积为 .‎ ‎6、如图所示，在△ABC中，AB=13，BC=10，BC边上的中线AD=12，∠B与∠C相等吗？为什么？‎ ‎7、（选做题）若△ABC的三边长为a，b，c满足a2+b2+c2+200=12a+16b+20c 根据条件判断△ABC的形状.‎ 9‎ 第一章 勾股定理 ‎1.3 勾股定理的应用 一、问题引入：‎ ‎1、勾股定理：直角三角形两直角边的 等于 .如果用a，b和c表示直角三角形的两直角边和斜边，那么 . ‎ ‎2、勾股定理逆定理：如果三角形三边长a，b，c满足 ，那么这个三角形是直角三角形.‎ 二、基础训练：‎ ‎1、在△ABC中，已知AB=12cm，AC=9cm，BC=15cm，则△ABC的面积等于（ ）‎ A.108cm2 B.90cm2 C.180cm2 D.54cm2 ‎ ‎2、五根小木棒，其长度分别为7，15，20，24，25，现将他们摆成两个直角三角形，其中正确的是（ ） ‎ 三、例题展示：‎ A B 例1：有一个圆柱，它的高等于12厘米，底面半径等于3厘米.在圆柱的底面A点有一只蚂蚁，它想吃到上底面上与A点相对的B点处的食物，沿圆柱侧面爬行的最短路程是多少？(π的值取3)。‎ ‎(1)如图2,将圆柱侧面剪开展开成一个长方形,从A点到B 点的最短路线是什么?你画对了吗?‎ ‎(2) 蚂蚁从点A出发，想吃到点B处的食物，它沿圆柱侧面爬行的最短路程是什么？‎ ‎ ‎ 9‎ 例2：如图，是一个滑梯示意图，若将滑梯AC水平放置，则刚好与AB一样长。已知滑梯的高度CE=3m，CD=1m，试求滑道AC的长.‎ 四、课堂检测：‎ ‎1、△ABC中，若AC＋AB= BC，则∠B＋∠C= .‎ ‎2、已知一个三角形的三边长分别是8cm，15cm，17cm，则这个三角形的面积为 .‎ ‎3、如果一个三角形的两条直角边之比是3∶4，且最小边的长度是6，最长边的长度是________.‎ ‎4、在△ABC中，AB＝8cm，BC＝15cm，要使∠B＝90°，则AC的长必为______cm.‎ ‎（第6题图）‎ ‎5、如图，一个三级台阶，它的每一级的长宽和高分别为20、3、2，A和B是这个台阶两个相对的端点，A点有一只蚂蚁，想到B点去吃可口的食物，则蚂蚁沿着台阶面爬到B点最短路程是　　　　.‎ ‎ ‎ ‎（第5题图）‎ ‎6、如图：有一圆柱，它的高等于8cm，底面直径等于4cm（）‎ 在圆柱下底面的点有一只蚂蚁，它想吃到上底面与相对的点处的食物，需要爬行的最短路程大约（ ）‎ A. 10cm 　B. 12cm 　　 C. 19cm 　 D. 20cm ‎7、如图，长方体的长为15 cm，宽为10 cm，高为20 cm，‎ 点B离点C 5 cm，一只蚂蚁如果要沿着长方体的表面从 点A爬到点B，需要爬行的最短距离是多少？ ‎ 第7题图 9‎ 第一章 ‎ 勾股定理单元检测 一、选择题：‎ ‎1、下列四组数据不能作为直角三角形的三边长的是（ ）‎ A．6、8、10 B. 5、12、13 C. 12、18、22 D. 9、12、15‎ ‎2、将直角三角形的三条边长同时扩大同一倍数，得到的三角形是( )‎ A.钝角三角形 B.锐角三角形 C.直角三角形 D.等腰三角形 ‎3、如果梯子的底端离建筑物5米,13米长的梯子可以达到该建筑物的高度是 ( ) ‎ A. 12米 B. 13米 C. 14米 D. 15米 ‎4、等腰三角形的一腰长为13,底边长为10,则它的面积为（ ）‎ 第4题图 A.65 B.60 C.120 D.130‎ ‎5、已知一直角三角形的木板，三边的平方和为1800cm2,则斜边长为（ ）‎ A. B. C. D.‎ ‎6、等边三角形的边长是10，它的高的平方等于（ ）‎ A.50 B.75 C.125 D.200‎ ‎7、直角三角形的两直角边分别为5厘米、12厘米，则斜边上的高是（ ）‎ A.6厘米 B.8厘米 C.厘米 D.厘米 ‎8、已知Rt△ABC中，∠C=90°，若a+b=14cm，c=10cm，则Rt△ABC的面积是（　　）‎ ‎ A. 24cm2 B. 36cm2 C. 48cm2 D. 60cm2‎ 二、填空题：‎ ‎9、△ABC中，若AC＋AB= BC，则∠B＋∠C= .‎ ‎10、若三角形的三边之比为3﹕4﹕5，则此三角形为 三角形.‎ ‎11、如图（1），∠OAB=∠OBC=∠OCD=90°， AB=BC=CD=1，OA=2，则OD2=____________.‎ ‎12、 如图（2）， 等腰△ABC的底边BC为16, 底边上的高AD为6，则腰AB的长为____________.‎ ‎13、如图（3），某人欲横渡一条河，由于水流的影响，实际上岸地点C偏离欲到达点B 300m，结果他在水中实际游了500m，求该河流的宽度为___________m.‎ ‎ ‎ 9‎ 三、解答题：‎ ‎14、如图所示，折叠长方形一边AD，点D落在BC边的点F处，‎ 已知BC=10厘米，AB=8厘米，求FC的长.‎ ‎ ‎ ‎15、如图所示，四边形ABCD中，∠ABC＝90０，AB＝4，BC＝3，CD＝12，AD＝13，求四边形ABCD的面积.‎ ‎16、甲、乙两位探险者到沙漠进行探险.某日早晨8:00甲先出发，他以6千米/时的速度向正东行走。1小时后乙出发，他以5千米/时的速度向正北行走.上午10：00，甲、乙二人相距多远?‎ 9‎ 9‎