八年级下数学课件《矩形、菱形、正方形》 (12)_苏科版 23页

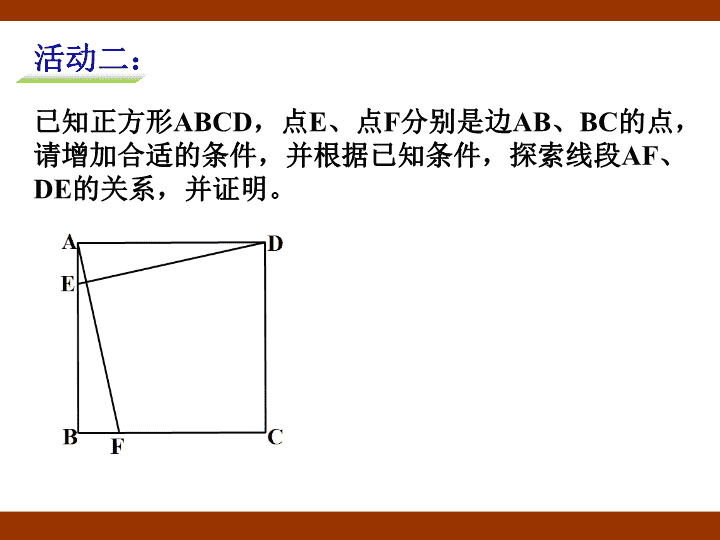
苏科版·八年级下册 活动一： 已知正方形ABCD，点E、点F分别是边AB、BC的中点， 探索线段AF、DE的关系，并证明。 已知正方形ABCD，点E、点F分别是边AB、BC的点， 请增加合适的条件，并根据已知条件，探索线段AF、 DE的关系，并证明。 活动二： 已知正方形ABCD，点E、点F、点G分别是边AB、BC、 AD上的点，请增加合适的条件，并根据已知条件，探 索线段GF、DE的关系。 活动三： 正方形ABCD的边长为18，在AD上取点G，在BC上 取点F，将这个正方形沿GF折叠，使点D落在边AB上， 得到点E，已知AE=6，求DG的长。 变式1： 在变式1中，DC经折叠后与边BC交于点H，随着点G、 点F在边AD、BC上移动，∠EDH的大小会发生改变吗？ 变式2： 已知正方形ABCD，点E、点F、点G、点H分别是边AB、 BC、AD、DC上的点，现在请你将GF EH和GF=EH中的 一个作为条件，另一个作为结论，编出正确的题目， 并给出证明。 活动四： 已知正方形ABCD，点E、点F分别是边AB、BC延长线 上的点，请利用线段AF、DE的数量和位置关系，编写 题目并给出证明。 活动五： 在上面的条件下，点G、H、M、N分别是AF、FE、DE、 DA的中点，请判断四边形GHMN的形状并证明。 变式1： 已知正方形ABCD，对角线AC、BD交于点O，点E、点F 分别是边AD、DC上的点，OE OF,假设正方形边长为1， 求线段EF的最小值。 活动六： 当 绕点O旋转时，四边形EOFD的面积发生改变吗？ 变式1： 已知正方形ABCD，点E是边BC的中点，点G是BC延长线 上的点，AE=EF，CF平分∠DCG，其中AE=EF，求证： AE EF 拓展提升： 若点E是边BC上的任意一点，AE=EF，CF平分∠DCG，将 AE=EF和AE EF中的一个作为条件，另一个作为结论， 编写题目，并给出证明。 变式1：  正方形的性质： 边： 角： 对边平行，四边相等 对称性： 对角线： 四个角都是直角 对角线相等并且互相垂直平分， 每条对角线平分一组对角 既是轴对称图形也是中心对称 图形 正方形的判定： 有一组邻边相等并且有一个角是直角的 平行四边形是正方形； 有一组邻边相等的矩形是正方形； 有一个角是直角的菱形是正方形. 正方形总结： 平行四边形 矩 形 菱 形正方形 正方形的性质： 边： 角： 对边平行，四边相等 对称性： 对角线： 四个角都是直角 对角线相等并且互相垂直平分， 每条对角线平分一组对角 既是轴对称图形也是中心对称 图形