八年级上数学课件《一次函数、一元一次方程和一元一次不等式》 (17)_苏科版 15页

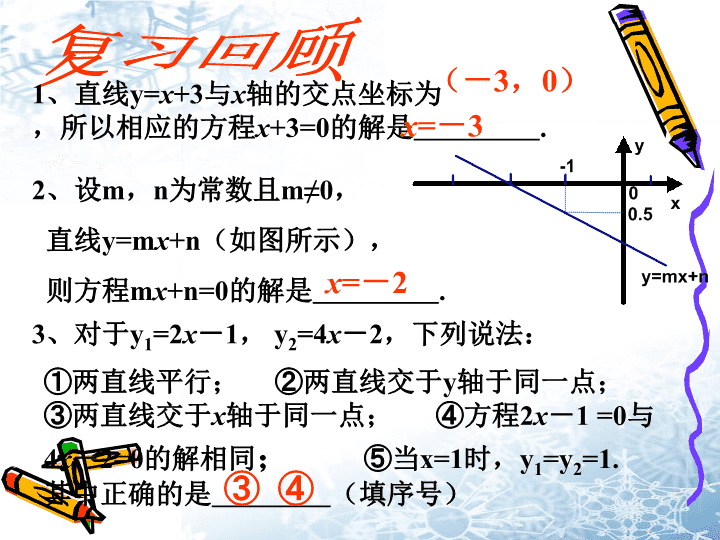
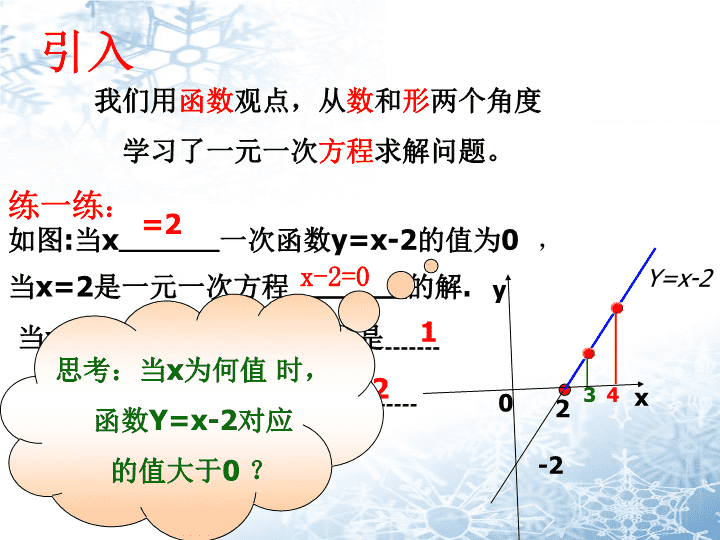
7.7一元一次不等式与一元一 次方程、一次函数 1、直线y=x+3与x轴的交点坐标为 ， 所以相应的方程x+3=0的解是 . 2、设m，n为常数且m≠0， 直线y=mx+n（如图所示）， 则方程mx+n=0的解是 . y=mx+n -1 0.5 0 y x 3、对于y1=2x－1， y2=4x－2，下列说法： ①两直线平行； ②两直线交于y轴于同一点； ③两直线交于x轴于同一点； ④方程2x－1 =0与 4x－2=0的解相同； ⑤当x=1时，y1=y2=1. 其中正确的是 （填序号） x=－3 （－3，0） x=－2 ③ ④ 练一练： 如图:当x——————一次函数y=x-2的值为0 ， 引入 当x=2是一元一次方程———————的解. =2 x-2=0 32 x -2 y 0 Y=x-2 4 当x=3时，函数y=x-2的值是-------1 当x=4，函数y=x-2的值是--------2 思考：当x为何值 时， 函数Y=x-2对应 的值大于0 ？ 我们用函数观点，从数和形两个角度 学习了一元一次方程求解问题。 探究： 解：(1)把5x+6>3x+10转化为2x-4>0，解得x >2 ⑵就是要解不等式2x-4>0，　解得x >2时 　　函数y=2x-4的值大于0 (1)解不等式：5x+6>3x+10 (2)当x为何值时，函数y=2x-4的值大于0 议一议：在上面的问题解 决过程中，你能发现它们 之间有什么关系吗？ 从数的角度看它 们是同一个问题 2.我们如何用函数图象来解决:5x+6>3x+10 解：化简得2x-4>0，画出直线y=2x-4, -4 2 y x0 Y=2x-4 可以看出，当x＞2时，这条 直线上的点在x轴的上方， 即这时y=2x-4>0。 从形的角度看 它们是同一个 问题 思考：　　问题1：解不等式ax+b>0 　　问题2：求自变量x在什么范围内，一次函数　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 y=ax+b的值大于0 上面两个问题有什么关系？　 　　从实践中得出，由于任何一元一次 不等式都可以转化为ax+b＞0或ax+b＜0 （a，b为常数，a≠0)的形式，所以解 一元一次不等式可以看作：当一次函数 y=ax+b的值大于0（或小于0）时，求自 变量相应的取值范围。 从数的角度看 求ax+b＞0(a≠0)的解 x为何值时y=ax+b的值大于0 从形的角度看 求ax+b＞0(a≠0)的解 　确定直线y=ax+b在x轴上方的 　　　　　　　　　　　　图象所对应的x的值 根据下列一次函数的图象，你能求出 哪些不等式的解集？并直接写出相应的 不等式的解集。 3x+6>0 ( x>- 2) 3x+6<0 ( x<- 2) 3x+6≥0 ( x ≥- 2) 3x+6≤0 ( x ≤ - 2) y x0-2 Y=3x+6 可以看出，当x<2时这条直线上的点在x轴的下方， 解：化简得3x-6<0，画出直线y=3x-6， 即这时y=3x-6<0，所以不等式的解集为x<2 例１.用画函数图象的方法解不等式　　　　 5x+4<2x+10 y x -6 20 Y=3x-6 尝试： 例2：已知函数Y1=5X+4，Y2=2X+10，求当 X为何值时，Y1=Y2？X为何值时，Y1 B 3.利用函数图象解不等式：3x－4＜x+2(用两种方法) 解法1：化简不等式得2x－6＜0，画出函 数y＝2x－6的图象，当x＜3时y＝2x－6＜ 0，所以不等式的解集为x＜3。 解法2：画出函数y＝3x－4和函 数y＝x+2的图象，交点横坐标为 3，当x＜3时，对于同一个x，直 线y＝3x－4上的点在直线y＝x+2 上相应点的下方，这表示3x－4 ＜x+2，所以不等式的解集为x ＜ 3。 y x0 -6 3 Y=2x-6 3 y x0 y＝x＋2 y＝3x－4 4、课本：第28页第3题 我们学校做一批校徽，需要拍照，若到照相馆拍，每张需要8元； 若学校自己拍，除买摄象机，需120元，每张还需成本4元，设 需要拍X张，到照相馆拍需要Y1 元，学校自己拍需要Y2元。 1.求Y1和Y2与X的函数关系式 2.问拍这批照片到照相馆拍，费用省还是由学校自己拍费用省？ 请说明理由。 解:(1) Y1＝8x,Y2=4x+120 (2)由图象可知，当x=30 时，两家一样， 当X>30时，照相馆省钱， 当X<30时，学校自己省钱. 30 y x0 Y=4x+120 Y=8x 五.小结一下 1.这节课我们学到了哪些知识？ 2.我们是用哪些方法获得这些知识的？ 3.你觉得还有什么问题需要继续讨论吗？