八年级数学上册第2章三角形2-5全等三角形第3课时角边角ASA课件 湘教版 17页

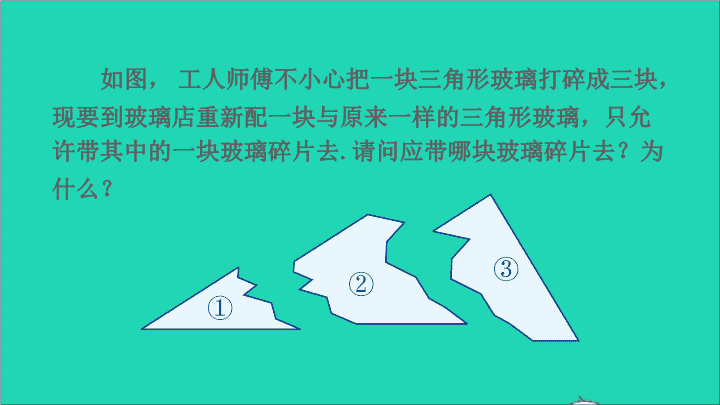
第3课时 角边角（ASA） 2 复习回顾 1.全等三角形的对应边、对应角有什么性质？ 全等三角形的对应边相等，对应角相等. 2.我们已经学过哪些判定两个三角形全等的方法？ ①定义 用定义证明两个三角形全 等不是很方便. ②SAS 如图， 工人师傅不小心把一块三角形玻璃打碎成三块， 现要到玻璃店重新配一块与原来一样的三角形玻璃，只允 许带其中的一块玻璃碎片去. 请问应带哪块玻璃碎片去？为 什么？ 推进新课 探究 如图，在△ABC和△A′B′C′中，BC=B′C′，∠B=∠B′， ∠C=∠C′，你能通过平移、旋转和轴反射等变换使△ABC 的像与△A′B′C′重合吗？△ABC与△A′B′C′全等吗？ A B C B′ C′ A ′ A B C B′ C′ A ′ 由上可见△ABC≌△A′B′C′. 类似于基本事实“SAS”的探究，同样地，我们可以通 过平移、旋转和轴反射等变换使△ABC的像与△A′B′C′重合. 结论 由此得到判定两个三角形全等的基本事实： 边角边定理 两角及其夹边分别相等的两个三角形全等. (可简写成“角边角”或“ASA”). 　　归纳概括“ASA”判定方法： 两角和它们的夹边分别相等的两个三角形全等（简 写为“角边角”或“ASA”）． 几何语言： 在△ABC 和△ A′B′ C′中， ∠A =∠A′， AB = A′B′， ∠B =∠B′， A B C || ||| | A′ B′ C′ || ||| | 已知：如图，点A，F，E，C在同一条直线上， AB∥DC，AB=CD，∠B=∠D. 求证：△ABE≌ △CDF. 例3 证明 ∵AB∥DC，∴∠A=∠C， 在△ABE和△CDF中， ∠A = ∠C， AB = CD， ∠B = ∠D， 如图，为测量河宽AB，小军从河岸的A点沿着与AB 垂直的方向走到C点，并在AC的中点E处立一根标杆，然 后从C点沿着和AC垂直的方向走到D点，使点D，E，B恰 好在一条直线上. 于是小军说：“CD的长就是河的宽度.” 你能说出这个道理吗？ 例4 解 在△AEB和△CED中， ∠A = ∠C = 90°， AE = CE， ∠AEB = ∠CED（对顶角相等）， 练习 已知： 如图，△ABC≌ △A′B′C′，CF， C′F′分别是 ∠ACB和∠A′C′B′的平分线. 求证： CF = C′F′. 证明 ∵△ABC≌ △A′B′C′， 在△FCA和△F′C′A′中， ∠FAC = ∠F′A′C′， AC = A′C′， ∠FCA = ∠F′C′A′， 巩固练习 1.已知：如图，∠ABC = ∠DEF， AB = DE，要证明△ABC≌ △DEF， （1）若以“SAS”为依据，还须添 加的一个条件为____________. （2）若以“ASA”为依据，还须添 加的一个条件为_____________. BC = EF ∠A =∠D 2. 判断. a.有两条边和一个角对应相等的两个三角形 全等. （ ） b.有两个角和一条边对应相等的两个三角形 全等. （ ） × √ 3.如图，已知AB=AE，∠1=∠2，∠B=∠E， 求证：BC=ED. A B E C D 1 2证明：∵∠1=∠2， ∴ ∠1+∠BAD=∠2+∠BAD， 即∠EAD=∠BAC. 在△AED和△ABC中， ∠E=∠B， AE=AB， ∠EAD=∠BAC， ∴△AED≌ △ABC(ASA)， ∴BC=ED（全等三角形的对应边相等） 课后小结 A B C || ||| | A′ B′ C′ || ||| | 两角及其夹边分别相等的两个三角形全等. (可简写成“角边角”或“ASA”).