八年级数学上册第14章全等三角形14-2三角形全等的判定（第2课时）课件（新版）沪科版 12页

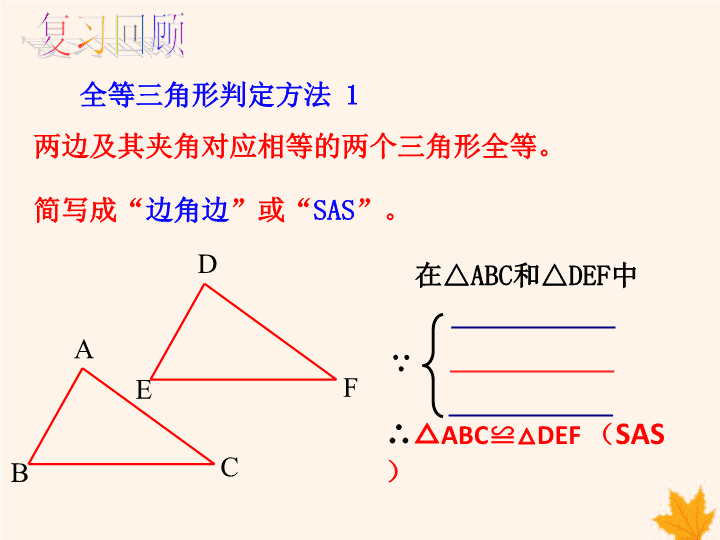
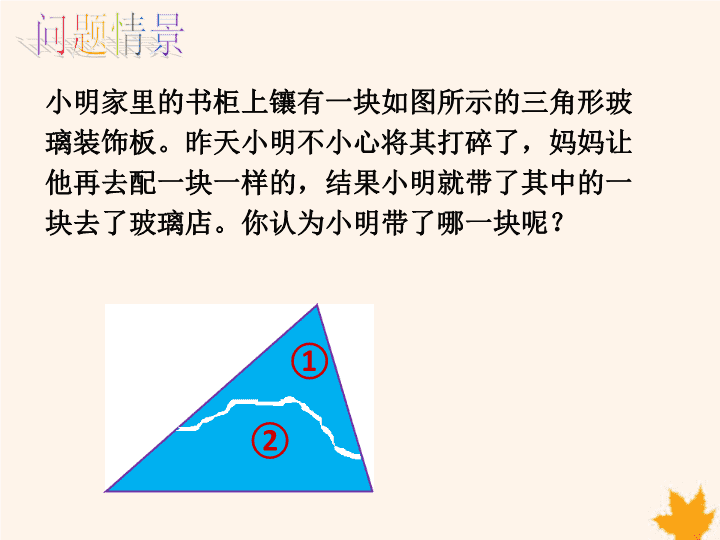
14.2 三角形全等的判定 第二课时 ASA 第十四章 A B C D E F 全等三角形判定方法 1 ∴△ABC≌△DEF （SAS） 两边及其夹角对应相等的两个三角形全等。 简写成“边角边”或“SAS”。 在△ABC和△DEF中 ∵ 小明家里的书柜上镶有一块如图所示的三角形玻 璃装饰板。昨天小明不小心将其打碎了，妈妈让 他再去配一块一样的，结果小明就带了其中的一 块去了玻璃店。你认为小明带了哪一块呢？ ① ② 画线段AB=5cm ， 再画∠BAP=45°， ∠ABQ=60°， AP与BQ相交于点C。 剪下所画的△ABC与 同桌进行比较。 A B PQ C 45° 60° 两角及其夹边对应相等的两个三 角形是否全等？ 画一个△ABC，使得AB=5cm， ∠A=45°,∠B=60°. 5cm 你能得到什么结论? P A B Q C 45° 60° 两角及其夹边对应相等的两个三 角形是否全等？ P A B Q C 45° 60° 5cm5cm 三角形全等判定方法 2 在△ABC与△DEF中 ∴ △ABC≌△DEF（ASA） 两角及其夹边对应相等的两个三角形全等。 简写成“角边角”或“ASA”。 ∠A=∠D AB=DE ∠B=∠E ∵ C A B 40° 60°cm5.4 D E F 40° 60°cm5.4 已知：如图，∠1＝∠2，∠3＝∠4.求证：DB=CB　　 证明：∵∠3 +∠5=180°,∠4 +∠6=180° ∴ ∠5=∠6（等角的补角相等） 在△ABD和△ABC中， ∴ △ABD ≌ △ABC （ ＡＳＡ） B D A C P 1 2 3 45 6 （平角定义） 又∵∠3 =∠4 （已知） ∠1=∠2 ( 已知 ) AB=AB (公共边) ∠5=∠6 ( 已证 ) ∵ ∴ DB = CB （全等三角形对应边相等） 证明： 在△ABC和△BAD中 ∵ ∠DAB=∠CBA (已证) AB = BA (公共边) ∴△ABC≌△BAD ( ASA ) 1.已知:如图，∠1=∠2，∠3=∠4， 求证：△ABC≌△BAD. 1 2 43 ∵ ∠1=∠2，∠3=∠4（已知） 即 ∠DAB = ∠CBA ∠1 = ∠2 (已知) ∴ ∠1+∠3=∠2+∠4（等式性质） 2.已知:如图，在△ABC中， AD平分∠BAC,AD⊥BC于点D， 求证：∠B=∠C. 1 2 3 4 在△ABD和△ACD中 ∵ ∠3 = ∠4 (已证) AD = AD (公共边) ∴△ABD≌△ACD ( ASA ) ∵ AD平分∠BAC（已知） ∠1 = ∠2 (已证) 证明： ∴∠1=∠2 (角平分线定义) ∵ AD⊥BC（已知） ∴∠3=∠4=90° (垂直定义) ∴∠B =∠C (全等三角形对应角相等) 3.已知:如图，点A、B、C、D在同一条直线上， AB=CD,AE⊥AD于A，BF⊥AD于B，CE∥DF. 求证：AE=BF. 1 2 已知:如图，A、B、C、D四点在同一条直线上，AB=CD, AE⊥AD于A，BF⊥AD于B，CE∥DF.求证：AE=BF. 1 2 在△ACE和△BDF中 ∵ ∠2 = ∠D (已证) AC = BD (已证) ∴△ACE≌△BDF( ASA ) ∵ AE⊥AD，BF⊥AD（已知） ∠A = ∠1 (已证) 证明： ∵ CE∥DF（已知） ∴∠2=∠D ∴AE =BF (全等三角形对应边相等) ∴∠A=∠1=90°(垂直定义) ∵ AB=CD （已知） ∴ AB+BC=CD+BC(等式性质) 即 AC=BD 2.在应用“ASA”时要注意：必须是对应的两 角及两角所夹的边相等。 1.角边角：两角和它们的夹边对应相等的两个 三角形全等(ASA)。 3.今后判定两条线段相等或两个角相等可以通 过证明它们所在的两个三角形全等而得到。 本节课你有什么收获？