八年级下册数学教案 1-2 第3课时 勾股定理的逆定理 湘教版 2页

第3课时　勾股定理的逆定理 ‎1．能利用勾股定理的逆定理判定一个三角形是否为直角三角形；(重点)‎ ‎2．灵活运用勾股定理及其逆定理解决问题．(难点)‎ 一、情境导入 古埃及人曾经用下面的方法画直角：将一根长绳打上等距离的13个结，然后如图那样用桩钉钉成一个三角形，他们认为其中一个角便是直角．‎ 你知道这是什么道理吗？‎ 二、合作探究 探究点一：勾股定理的逆定理 ‎【类型一】 勾股数 ‎ 判断下列几组数中，一定是勾股数的是(　　)‎ ‎　　　　　　　　　　　　　　　‎ A．1，， B．8，15，17‎ C．7，14，15 D.，，1‎ 解析：选项A不是，因为和不是正整数；选项B是，因为82＋152＝172，且8、15、17是正整数；选项C不是，因为72＋142≠152；选项D不是，因为与不是正整数．故选B.‎ 方法总结：勾股数必须满足：①三个数必须是正整数，例如：2.5、6、6.5满足a2＋b2＝c2，但是2.5、6.5不是正整数，所以它们不是勾股数；②一组勾股数扩大相同的整数倍得到三个数仍是一组勾股数．‎ ‎【类型二】 判断三角形的形状 ‎ 已知a，b，c为△ABC的三边，且满足(a－7)2＋(b－24)2＋(c－25)2＝0.试判断△ABC的形状．‎ 解析：可先确定a，b，c的值，然后再结合勾股定理的逆定理进行判断．‎ 解：由平方数的非负性，得a－7＝0，b－24＝0，c－25＝0.∴a＝7，b＝24，c＝25.又∵a2＝72＝49，b2＝242＝576，c2＝252＝625，∴a2＋b2＝c2.∴△ABC是直角三角形．[来源:Z,xx,k.Com]‎ 方法总结：此题主要依据“若几个非负数的和为0，则这几个非负数同时为0”这一性质来确定a，b，c的值．该知识点在解题时会经常用到，应注意掌握．‎ ‎【类型三】 利用勾股定理逆定理解决与角有关的问题[来源:学#科#网Z#X#X#K]‎ ‎ 在如图的方格中，△ABC的顶点A、B、C都是方格线的交点，则三角形ABC的外角∠ACD的度数等于(　　)‎ A．130° B．135°‎ C．140° D．145°‎ 解析：∵AB2＝12＋22＝5，BC2＝12＋22＝5，AC2＝12＋32＝10，∴AC2＝AB2＋BC2，∴△ABC是等腰直角三角形，∵∠ACD是△ABC的外角，∴∠ACD＝∠A＋∠B＝45°＋90°＝135°.故选B.‎ 方法总结：在网格图中求三角形的角度时可以运用勾股定理和一些特殊角的边角关系来解答，比如在直角三角形中30°所对的直角边是斜边的一半，45°的直角三角形中两直角边相等．‎ ‎【类型四】 运用勾股定理的逆定理解决面积问题 ‎ 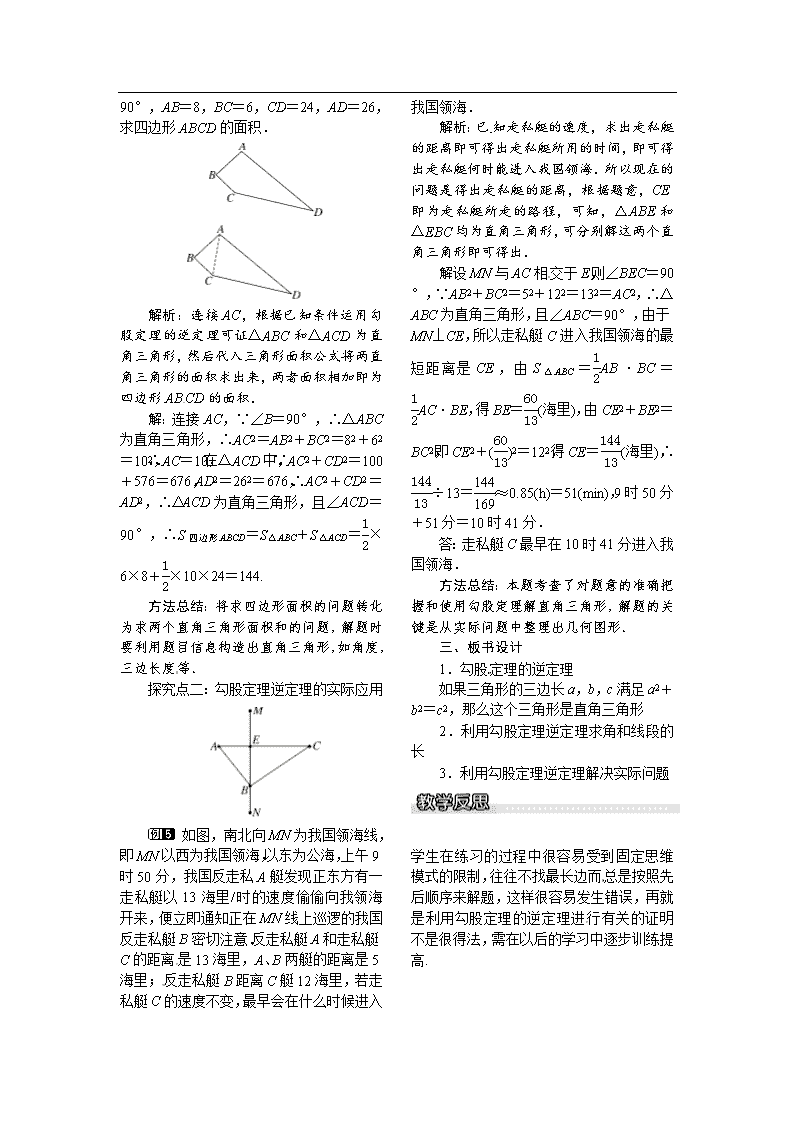如图，在四边形ABCD中，∠B ‎＝90°，AB＝8，BC＝6，CD＝24，AD＝26，求四边形ABCD的面积．‎ ‎　　　[来源:学科网]‎ 解析：连接AC，根据已知条件运用勾股定理的逆定理可证△ABC和△ACD为直角三角形，然后代入三角形面积公式将两直角三角形的面积求出来，两者面积相加即为四边形ABCD的面积．‎ 解：连接AC，∵∠B＝90°，∴△ABC为直角三角形，∴AC2＝AB2＋BC2＝82＋62＝102，∴AC＝10，在△ACD中，∵AC2＋CD2＝100＋576＝676，AD2＝262＝676，∴AC2＋CD2＝AD2，∴△ACD为直角三角形，且∠ACD＝90°，∴S四边形ABCD＝S△ABC＋S△ACD＝×6×8＋×10×24＝144.‎ 方法总结：将求四边形面积的问题转化为求两个直角三角形面积和的问题，解题时要利用题目信息构造出直角三角形，如角度，三边长度等．‎ 探究点二：勾股定理逆定理的实际应用 ‎ 如图，南北向MN为我国领海线，即MN以西为我国领海，以东为公海，上午9时50分，我国反走私A艇发现正东方有一走私艇以13海里/时的速度偷偷向我领海开来，便立即通知正在MN线上巡逻的我国反走私艇B密切注意．反走私艇A和走私艇C的距离是13海里，A、B两艇的距离是5海里；反走私艇B距离C艇12海里，若走私艇C的速度不变，最早会在什么时候进入我国领海．‎ 解析：已知走私艇的速度，求出走私艇的距离即可得出走私艇所用的时间，即可得出走私艇何时能进入我国领海．所以现在的问题是得出走私艇的距离，根据题意，CE即为走私艇所走的路程，可知，△ABE和△EBC均为直角三角形，可分别解这两个直角三角形即可得出．‎ 解：设MN与AC相交于E，则∠BEC＝90°，∵AB2＋BC2＝52＋122＝132＝AC2，∴△ABC为直角三角形，且∠ABC＝90°，由于MN⊥CE，所以走私艇C进入我国领海的最短距离是CE，由S△ABC＝AB·BC＝AC·BE，得BE＝(海里)，由CE2＋BE2＝BC2，即CE2＋()2＝122，得CE＝(海里)，∴÷13＝≈0.85(h)＝51(min)，9时50分＋51分＝10时41分．‎ 答：走私艇C最早在10时41分进入我国领海．‎ 方法总结：本题考查了对题意的准确把握和使用勾股定理解直角三角形，解题的关键是从实际问题中整理出几何图形．‎ 三、板书设计 ‎1．勾股定理的逆定理 如果三角形的三边长a，b，c满足a2＋b2＝c2，那么这个三角形是直角三角形 ‎2．利用勾股定理逆定理求角和线段的长 ‎3．利用勾股定理逆定理解决实际问题 ‎[来源:学科网][来源:学科网ZXXK]‎ 学生在练习的过程中很容易受到固定思维模式的限制，往往不找最长边而总是按照先后顺序来解题，这样很容易发生错误，再就是利用勾股定理的逆定理进行有关的证明不是很得法，需在以后的学习中逐步训练提高.‎