八年级上数学课件八年级上册数学课件《一定是直角三角形吗》 北师大版 (2)_北师大版 21页

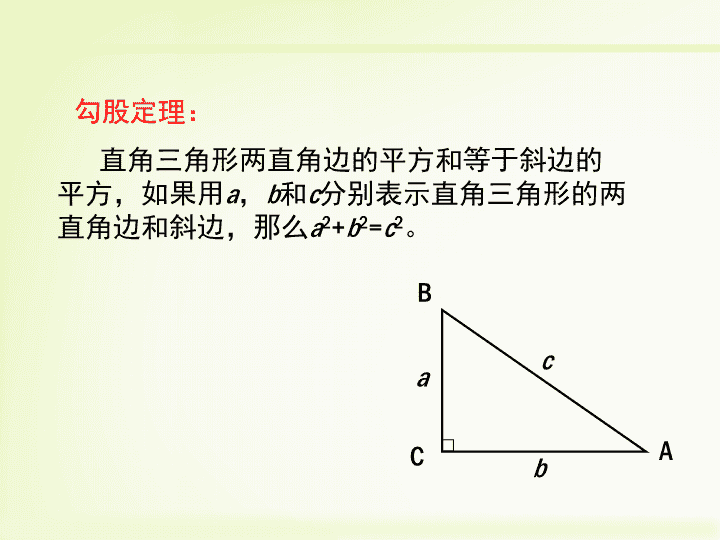
1.2 一定是直角三角形吗 第一章 勾股定理 C o n t e n t s 目录 01 02 03 04 复习旧知 巩固练习 课堂小结 新知探究 问题解决 05 问题情境 06 勾股定理： 直角三角形两直角边的平方和等于斜边的 平方，如果用a，b和c分别表示直角三角形的两 直角边和斜边，那么a2+b2=c2。 A B C a b c 古埃及人常用结绳方法构建直角三角形 一根绳平均分成12节， 构成下面的三角形： 这是直角三角形吗？ 3 4 5 如果a2+b2=c2，那么这个三角形是直角三角形吗？ A B C a b c 用a，b，c分别表示三角形的三边 做一做 下面的每组数分别是一个三角形的三边长a，b，c， 而且都满足a2+b2=c2 ： ① 3，4，5 ② 5，12，13 ③ 8，15，17 分别以每组数为三边作出三角形，用量角器 量一量，你有什么发现？ 9+16=25 25+144=169 64+225=289 已知：在△ABC中，三边长分别为a，b，c，且a2+b2=c2， 你能否判断△ABC是直角三角形？并说明理由。 A B C a b c MC` N A` B` a b a2+b2=c2=AB2 A`B`2= a2+b2 ∴△ABC≌ △A`B`C` ∴∠C=90° 新知归纳 “勾股定理”逆定理： (1)文字语言：如果三角形的三边长a，b，c满足 a2+b2=c2，那么这个三角形是直角三角形。 A B C a b c ∵a2+b2=c2(已知) (2)符号语言： ∴∠C=90°(勾股定理逆定理) 拓广探索 下列几组数据能否作为直角三角形的三边？ (1) 9，12，15; (2) 15，36，39; (3) 12，35，36 ; (4) 12，18，22。 (1) 92+122=152 能作为直角三角形的三边 (2) 152+362=392 能作为直角三角形的三边 (3) 122+352≠362 不能作为直角三角形的三边 (4) 122+182≠222 不能作为直角三角形的三边 92+122=152 以上两组数有什么特点？ 152+362=392 1、都是正整数； (1) 9，12，15; (2) 15，36，39; 2、都满足a2+b2=c2。 新知归纳 “勾股数”的定义： 满足a2+b2=c2的三个正整数，称为勾股数。 这是直角三角形 3 4 5 古埃及人常用结绳方法构建直角三角形 一根绳平均分成12节， 构成下面的三角形： 例1、一个零件的形状如图(1)所示，按规定这个 零件中∠A和∠DBC都应为直角，工人师傅量得 这个零件各边尺寸如图(2)所示，这个零件合格吗？ 图(1) 图(2) 新知归纳 “勾股定理”逆定理的应用： 已知三边特殊关系，判定直角三角形。 1、如果三条线段a，b，c满足a2=c2- b2，这三条 线段组成的三角形是直角三角形吗？为什么？ 2、如图，在正方形ABCD中，AB=4，AE=2， DF=1，图中有几个直角三角形，你是如何判断 的？与你的同伴交流。 4 2 2 1 3 4 BE2=42+22=20 FE2=12+22=5 FB2=32+42=25 BE2+FE2=FB2 3、如图，哪些是直角三角形，哪些不是，说说 你的理由？ 4、(1)如果将直角三角形的三边长同时扩大一个相 同的倍数，得到的三角形还是直角三角形吗？ 4、(2)下表中第一列每组数都是勾股数，补全下表， 这些数的2倍、3倍、4倍、10倍还是勾股数吗？任意倍 呢？说说你的理由。 “勾股定理”逆定理： (1)文字语言：如果三角形的三边长a，b，c满足 a2+b2=c2，那么这个三角形是直角三角形。 A B C a b c ∵a2+b2=c2(已知) (2)符号语言： ∴∠C=90°(勾股定理逆定理) “勾股定理”逆定理的应用： 已知三边特殊关系，判定直角三角形。 “勾股数”的定义： 满足a2+b2=c2的三个正整数，称为勾股数。