八年级上数学课件八年级上册数学课件《三角形内角和定理的证明》 北师大版 (1)_北师大版 14页

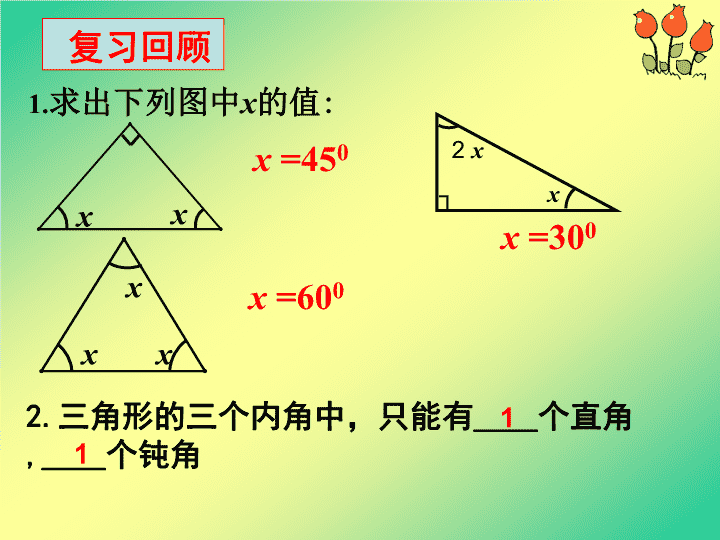
2.三角形的三个内角中，只能有____个直角 ,____个钝角 1 1.求出下列图中x的值: x x x x =600 x x x =450 2 x x┐ x =300 1 4.∠A=50°，∠B=∠C，则△ABC中∠B=____ 3.△ABC中，∠C=90°，∠A=30°，∠B=____60° 65° 5.三角形中三角之比为1∶2∶3，则三个角 各为多少度？ 解：设较小的角为x，则其余两个角分别为2x，3x 则x+2x+3x=180° 6x=180° X=30° 2x=60° 3x=90° 所以这三个角各为30°，60°，90° 每个学生拿出课前准备的三角形纸片，你 有哪些方法验证三角形内角和定理？与同伴交 流，并把你的方法展示给大家。 图1 A B C A B A B C B 图 2 B C CB A 你能结合图7—13写出已知、求证并证明 三角形内角和定理吗？ 用严谨的证明来论证三角形内角和定理 已知：如图7-13，△ABC 求证：∠A+∠B+∠C=180° 证明：延长BC到D，过点C作射线CE∥AB 则 ∠1=∠A（两直线平行，内错角相等） ∠2=∠B（两直线平行，同位角相等） ∵∠ACB+∠1+∠2=180°（平角的定义） ∴∠ACB+∠A+∠B=180°（等量代换） 你还能用其他方法证明三角形内角和 定理吗？小组内交流，并说说你的证明过 程。 ∴∠B+∠BAC+∠C=180°（等量代换） 证明：过点A作PQ∥BC 则∠PAB=∠B（两直线平行，内错角相等） ∠QAC=∠C（两直线平行，内错角相等） ∵∠PAB+∠BAC+∠QAC=180°（平角的定义） 例：已知：如图， 在△ABC 中，∠B= 38°，∠C=62°， AD是△ABC 的角平分线，求∠ADB的度数 解：在△ABC中 ∠B+∠C +∠BAC=180°（三角形内角和定理） ∵ ∠B= 38°， ∠C=62°（已知） ∴ ∠BAC=180°- ∠B- ∠C =180°- 38°- 62° =80°（等式的性质） ∵ AD平分∠BAC（已知） ∴ ∠BAD= ∠BAC= ×80°=40°（角平分线的定义） 在△ABD中 ∠B+∠BAD +∠ADB=180°（三角形内角和定理） ∵ ∠B= 38°（已知）， ∠BAD= 40°（已证） ∴ ∠ADB=180°- 38°- 40°=102°（等式的性质） ∴ ∠ADB的度数为102° 2 1 2 1 1.直角三角形的两锐角之和是多少度？请证明你的 结论. 已知：在Rt△ABC 中，∠C=90° 求证：∠A+∠B=90° 证明：在△ABC 中， ∠A+∠B+∠C=180°（三角形内角和定理） ∵ ∠C=90°（已知） ∴∠A+∠B=180°-∠C =180°-90° =90°（等式的性质） 直角三角形的两锐角之和是90° C A B 2.如图，已知，在△ABC中，DE∥BC， ∠A=60°,∠C=70°,求证：∠ADE=50°. 3.已知：△ABC中，∠C=∠B=2∠A （1）求∠B的度数； （2）若BD是AC边上的高，求∠DBC的度数？ 4.已知，如图，在Rt△ABC中，∠ACB=90°， CD⊥AB，垂足为D 求证：∠A=∠DCB 72° 18° 2题图 C A D B 4题图 解：∵∠A+∠ABC+∠ACB=180°（三角形内角和定理） ∴∠ABC+∠ACB=180°-∠A=180°-65°=115° ∵BF平分∠ABC，CF平分∠ACB（已知） ∴∠FBC= ∠ABC，∠FCB= ∠ACB（角平分线的定义） ∴∠FBC+∠FCB= （∠ABC+∠ACB） = ×115° =57.5° ∵∠BFC+∠FBC+∠FCB=180°（三角形内角和定理） ∴∠BFC=180°-(∠FBC+∠FCB)=180°-57.5°=122.5° ∴∠F的度数为122.5° 2 1 2 1 2 1 2 1 5.如图，在△ABC中，BF平分∠ABC，CF平分 ∠ACB，∠A=65°，求∠F的度数 A C F B 本节课收获 1、三角形内角和的定理：三角形的内角和等于180° 2、通过思考、去探究、去总结三角形内角和的定理， 并且发现要证明三角形三个内角的和等于180 °需 转化为：平角或两直线平行同旁内角和等于180°。 3、三角形内角和的定理证明中，添加辅助线的实质 是通过平行线来移动角。 　　教材P180习题7.6 1,3题