人教版八年级数学上册同步测试题及答案 (4) 4页

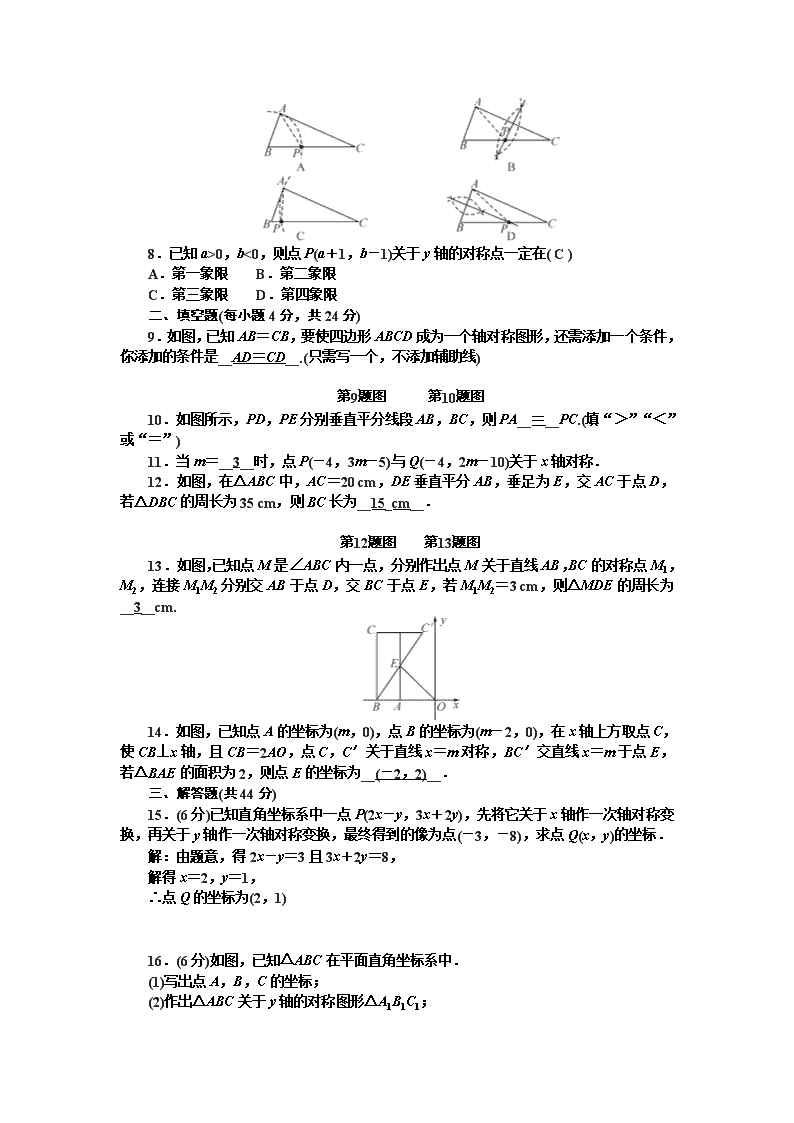
检测内容：13.1－13.2‎ 得分________　卷后分________　评价________‎ ‎　　　　　 　　　　　　　　　　　　　‎ 一、选择题(每小题4分，共32分)‎ ‎1．(湘西州中考)下列四个图形中，是轴对称图形的是( D )‎ ‎2．如图，直线l是五边形ABCDE的对称轴，其中∠C＝100°，∠ABC＝130°，那么∠BEA的度数等于( B )‎ A.45°‎ B．50°‎ C．60°‎ D．65°‎ ‎3．下面两点中，关于y轴对称的是( B )‎ A．A1(－1，3)，B1(1，－5)‎ B．A1(3，－5)，B1(－3，－5)‎ C．A1(－2，4)，B1(2，－4)‎ D．A1(5，－3)，B1(5，3)‎ ‎4．如图，△ABC和△A′B′C′关于直线l对称，下列结论中正确的有( B )‎ ‎①△ABC≌△A′B′C′；②∠BAC＝∠B′A′C′；③直线l垂直平分CC′；④直线BC和B′C′的交点不一定在直线l上．‎ A．4个 B．3个 C．2个 D．1个 　　　 ‎5．如图，将三角形纸片ABC沿直线DE折叠后，使得点B与点A重合，折痕分别交BC，AB于点D，E.如果AC＝5 cm，△ADC的周长为17 cm，那么BC的长为( C )‎ A．7 cm B．10 cm C．12 cm D．22 cm ‎6．(西宁中考)在平面直角坐标系中，将点A(－1，－2)向右平移3个单位长度得到点B，则点B关于x轴的对称点B′的坐标为( B )‎ A．(－3，－2) B．(2，2)‎ C．(－2，2) D．(2，－2)‎ ‎7．如图，已知△ABC(AC＜BC)，用尺规在BC上确定一点P，使PA＋PC＝BC，则下列四种不同方法的作图中准确的是( D )‎ ‎8．已知a>0，b<0，则点P(a＋1，b－1)关于y轴的对称点一定在( C )‎ A．第一象限 B．第二象限 C．第三象限 D．第四象限 二、填空题(每小题4分，共24分)‎ ‎9．如图，已知AB＝CB，要使四边形ABCD成为一个轴对称图形，还需添加一个条件，你添加的条件是__AD＝CD__.(只需写一个，不添加辅助线)‎ 　　　 ‎10．如图所示，PD，PE分别垂直平分线段AB，BC，则PA__＝__PC.(填“＞”“＜”或“＝”)‎ ‎11．当m＝__3__时，点P(－4，3m－5)与Q(－4，2m－10)关于x轴对称．‎ ‎12．如图，在△ABC中，AC＝20 cm，DE垂直平分AB，垂足为E，交AC于点D，若△DBC的周长为35 cm，则BC长为__15_cm__．‎ 　　 ‎13．如图，已知点M是∠ABC内一点，分别作出点M关于直线AB，BC的对称点M1，M2，连接M1M2分别交AB于点D，交BC于点E，若M1M2＝3 cm，则△MDE的周长为__3__cm.‎ ‎14．如图，已知点A的坐标为(m，0)，点B的坐标为(m－2，0)，在x轴上方取点C，使CB⊥x轴，且CB＝2AO，点C，C′关于直线x＝m对称，BC′交直线x＝m于点E，若△BAE的面积为2，则点E的坐标为__(－2，2)__．‎ 三、解答题(共44分)‎ ‎15．(6分)已知直角坐标系中一点P(2x－y，3x＋2y)，先将它关于x轴作一次轴对称变换，再关于y轴作一次轴对称变换，最终得到的像为点(－3，－8)，求点Q(x，y)的坐标．‎ 解：由题意，得2x－y＝3且3x＋2y＝8，‎ 解得x＝2，y＝1，‎ ‎∴点Q的坐标为(2，1)‎ ‎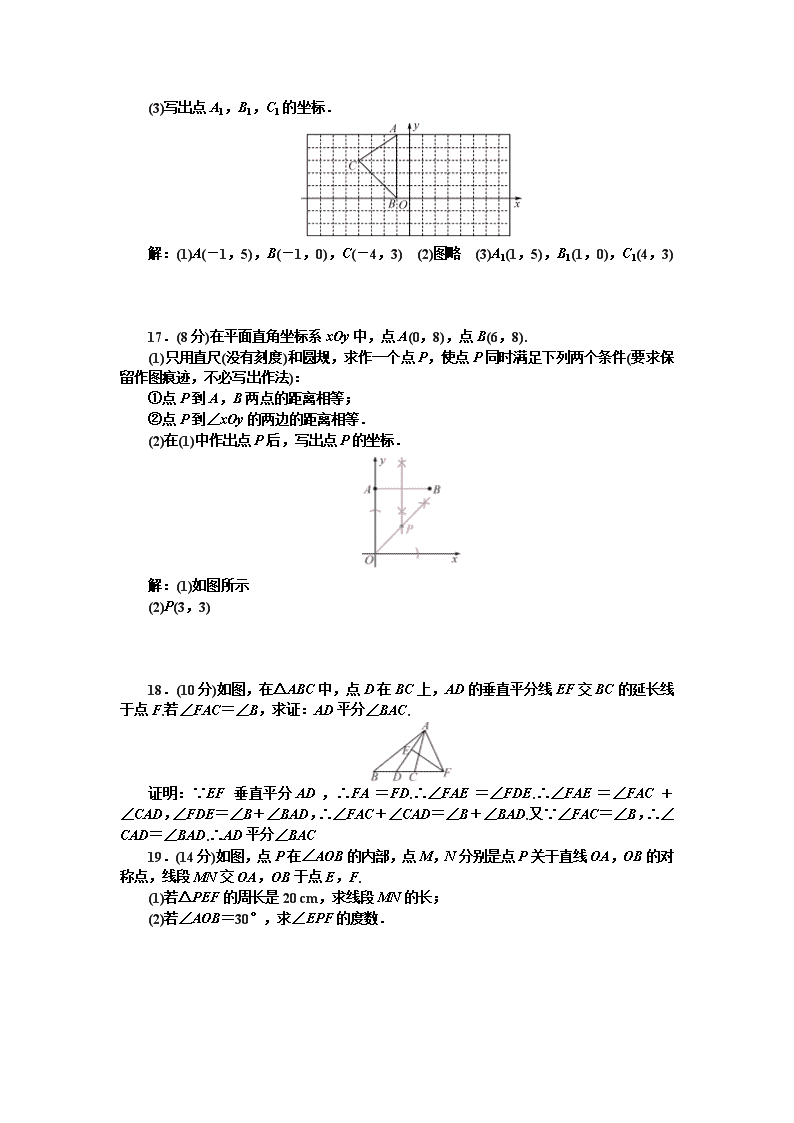16．(6分)如图，已知△ABC在平面直角坐标系中．‎ ‎(1)写出点A，B，C的坐标；‎ ‎(2)作出△ABC关于y轴的对称图形△A1B1C1；‎ ‎(3)写出点A1，B1，C1的坐标．‎ 解：(1)A(－1，5)，B(－1，0)，C(－4，3)　(2)图略　(3)A1(1，5)，B1(1，0)，C1(4，3)‎ ‎17．(8分)在平面直角坐标系xOy中，点A(0，8)，点B(6，8).‎ ‎(1)只用直尺(没有刻度)和圆规，求作一个点P，使点P同时满足下列两个条件(要求保留作图痕迹，不必写出作法)：‎ ‎①点P到A，B两点的距离相等；‎ ‎②点P到∠xOy的两边的距离相等．‎ ‎(2)在(1)中作出点P后，写出点P的坐标．‎ 解：(1)如图所示 ‎(2)P(3，3)‎ ‎18．(10分)如图，在△ABC中，点D在BC上，AD的垂直平分线EF交BC的延长线于点F.若∠FAC＝∠B，求证：AD平分∠BAC.‎ 证明：∵EF垂直平分AD，∴FA＝FD.∴∠FAE＝∠FDE.∴∠FAE＝∠FAC＋∠CAD，∠FDE＝∠B＋∠BAD，∴∠FAC＋∠CAD＝∠B＋∠BAD.又∵∠FAC＝∠B，∴∠CAD＝∠BAD.∴AD平分∠BAC ‎19．(14分)如图，点P在∠AOB的内部，点M，N分别是点P关于直线OA，OB的对称点，线段MN交OA，OB于点E，F.‎ ‎(1)若△PEF的周长是20 cm，求线段MN的长；‎ ‎(2)若∠AOB＝30°，求∠EPF的度数．‎ 解：(1)∵点M与点P关于OA对称，∴OA垂直平分MP.∴EM＝EP.又∵点N与点P关于OB对称，∴OB垂直平分PN.∴FP＝FN.∴MN＝EM＋EF＋FN＝EP＋EF＋FP＝△PEF的周长＝20 cm ‎(2)连接OM，ON，OP，∵OA垂直平分MP，∴OM＝OP.又∵OB垂直平分PN，∴ON＝OP.又∵ME＝PE，OE＝OE，PF＝NF，OF＝OF，∴△MOE≌△POE，△POF≌△NOF，∴∠MOE＝∠POE，∠OME＝∠OPE，∠POF＝∠NOF，∠OPF＝∠ONF.∴∠MON＝2∠AOB＝60°，∴∠EPF＝∠OPE＋∠OPF＝∠OME＋∠ONF＝180°－∠MON＝120°‎