【精品试题】人教版 八年级下册数学 第十八章 平行四边形周周测7（18 8页

第 1 页 共 8 页 第十八章 平行四边形周周测 7 一 选择题 1.如图,在▱ ABCD中,E、F、G、H分别是各边的中点,在下列四个图形中,阴影部分的面积与 其他三个阴影部分面积不相等的是（ ） A. B. C. D. 2.小明在学习了正方形之后,给同桌小文出了道题,从下列四个条 件:①AB=BC;②∠ABC=90°;③AC=BD;④AC⊥BD.中选两个作为补充条件,使▱ ABCD为正 方形（如图）,现有下列四种选法,你认为其中错误的是（ ） A.①② B.②③ C.①③ D.②④ 3.如图,在一个由 4×4 个小正方形组成的正方形网格中,阴影部分面积与正方形ABCD的面积 比是( ) A.3：4 B.5：8 C.9：16 D.1：2 4.如图,在正方形ABCD外侧,作等边三角形ADE,AC,BE相交于点F,则∠BFC为( ) A.75° B.60° C.55° D.45° 5.如图,将边长为 的正方形 ABCD 沿对角线 AC 平移,点 A 移至线段 AC 的中点 A′处,得新 正方形 A′B′C′D′,新正方形与原正方形重叠部分（图中阴影部分）的面积是（ ） A. B. C.1 D. 第 2 页 共 8 页 6.如图,将正方形OABC放在平面直角坐标系中,O是原点,若点A的坐标为(1, ),则点C坐标为 ( ) A.( ,1) B.(-1, ) C.(- ,1) D.(- ，-1) 7.如图,E是边长为l的正方形ABCD的对角线BD上一点,且BE=BC,P为CE上任意一点,PQ⊥BC 于点Q,PR⊥BE于点R,则PQ+PR的值为（ ） A. B. C. D. 8.如图,边长为 1 的正方形ABCD绕点A逆时针旋转 45 度后得到正方形AB′C′D′,边B′C′与DC交 于点O,则四边形AB′OD的周长是（ ） A.2 B.3 C. D.1+ 9.如图,正方形ABCD的面积为 12,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上 有一点P,使PD+PE的和最小,则这个最小值为（ ） A. B. C. D. 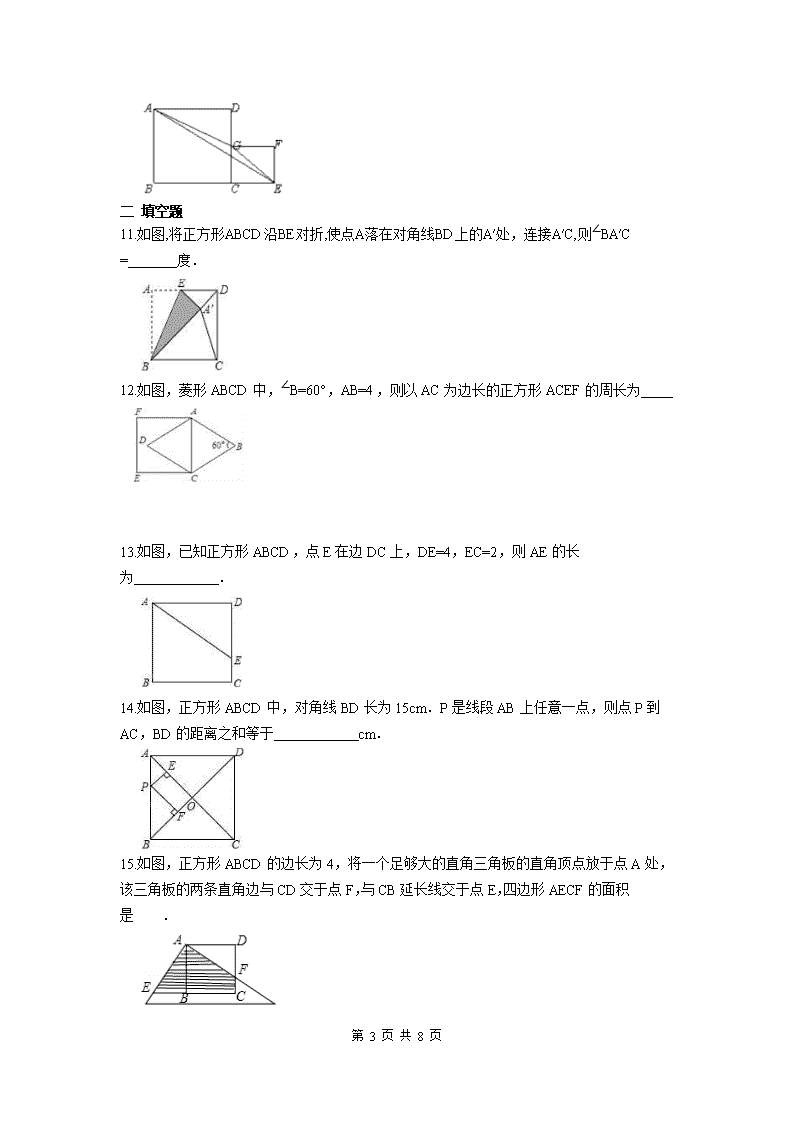10.如图,正方形ABCD和CEFG的边长分别为m、n,那么∆AEG的面积的值 （ ） A.与m、n的大小都有关 B.与m、n的大小都无关 C.只与m的大小有关 D.只与n的大小有关 第 3 页 共 8 页 二 填空题 11.如图,将正方形ABCD沿BE对折,使点A落在对角线BD上的A′处，连接A′C,则∠BA′C = 度． 12.如图，菱形 ABCD 中，∠B=60°，AB=4，则以 AC 为边长的正方形 ACEF 的周长为 13.如图，已知正方形 ABCD，点 E 在边 DC 上，DE=4，EC=2，则 AE 的长为 ． 14.如图，正方形 ABCD 中，对角线 BD 长为 15cm．P 是线段 AB 上任意一点，则点 P 到 AC，BD 的距离之和等于 cm． 15.如图，正方形 ABCD 的边长为 4，将一个足够大的直角三角板的直角顶点放于点 A 处， 该三角板的两条直角边与 CD 交于点 F，与 CB 延长线交于点 E，四边形 AECF 的面积是 ． 16.已知正方形 ABCD 中，点 E 在边 DC 上，DE＝2，EC＝1（如图所示），把线段 AE 绕点 A 旋转，使点 E 落在直线 BC 上的点 F 处，则 F、C 两点的距离为 ． 第 4 页 共 8 页 17.如图,在Rt△ABC中,∠ACB＝90°,以AC为边正方形面积为 12,中线CD长度为 2,则BC长度 为 ． 18.如图,点E在正方形ABCD的边CD上.若△ABE的面积为 8,CE=3,则线段BE的长为 ． 19.如图,在边长为 4 的正方形ABCD中,E是AB边上的一点,且AE=3,点Q为 对角线AC上的动点, 则△BEQ周长的最小值为 ． 20.如图,已知正方形ABCD边长为 3,点E在AB边上且BE=1,点P,Q分别是边BC,CD的动点（均 不与顶点重合），当四边形AEPQ的周长取最小值时，四边形AEPQ的面积是______． 21.如图,Rt△ABC中,∠C=90°,以斜边AB为边向外作正方形ABDE,且正方形对角线交于点O, 连接OC,已知AC=5,OC=6 ，则另一直角边BC的长为 ． 三 解答题 22.如图,在正方形 ABCD 中,BC=2,E 是对角线 BD 上的一点,且 BE=AB.求△EBC 的面积． 第 5 页 共 8 页 23.如图,E、F、 G、H分别为四边形ABCD四边之中点. (1)求证：四边形EFGH为平行四边形； (2)当AC、BD满足 时，四边形EFGH为菱形； 当AC、BD满足 时，四边形EFGH为矩形； 当AC、BD满足 时，四边形EFGH为正方形． 24.如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作 DE⊥BC,交直线MN于E,垂足为F,连接CD、BE． （1）求证：CE=AD； （2）当D在AB中点时，四边形BECD是什么特殊四边形？说明你的理由； 第 6 页 共 8 页 （3）若D为AB中点，则当∠A的大小满足什么条件时，四边形BECD是正方形？请说明你的 理由． 第十八章 平行四边形周周测 7 试题答案 1.C 2.B 3.B 4.B 5.B 6.C 7.A 8.A 9.B 10.D 11.67.5． 12.16； 13. 2 13 ． 14.7.5.cm．15.16． 16.1 或 5. 17.2 18.5． 19.6 20.4.5． 21.7． 第 7 页 共 8 页 22.解：作 EF⊥BC 于 F，如图所示：则∠EFB=90°， ∵四边形 ABCD 是正方形，∴AB=BC=2，∠DAB=∠ABC=90°， ∴∠ABD=∠DBC= ∠ABC=45°，∴△BEF 是等腰直角三角形，∴EF=BF， ∵BE=AB，∴BE=BC=2，∴EF=BF= BE= ，∴△EBC 的面积= BC•EF= ×2× = ． 23.（1）证明：如图，连接 BD， ∵E、F、G、H 分别为四边形 ABCD 四边之中点， ∴EH 是△ABD 的中位线，FG 是△BCD 的中位线， ∴EH∥BD 且 EH=12BD，FG∥BD 且 FG=12BD， ∴EH∥FG 且 EH=FG， ∴四边形 EFGH 为平行四边形； （2）AC=BD；AC⊥BD；AC=BD 且 AC⊥BD 解析：连接 AC， 同理可得 EF∥AC 且 EF=12AC， 所以，AC=BD 时，四边形 EFGH 为菱形； AC⊥BD 时，四边形 EFGH 为矩形； AC=BD 且 AC⊥BD 时，四边形 EFGH 为正方形． 故答案为：AC=BD；AC⊥BD；AC=BD 且 AC⊥BD． 24.（1）证明：∵DE⊥BC，∴∠DFB=90°， ∵∠ACB=90°，∴∠ACB=∠DFB，∴AC∥DE， ∵MN∥AB，即CE∥AD，∴四边形ADEC是平行四边形，∴CE=AD； （2）解：四边形BECD是菱形，理由是：∵D为AB中点，∴AD=BD， ∵CE=AD，∴BD=CE，∵BD∥CE，∴四边形BECD是平行四边形， ∵∠ACB=90°，D为AB中点，∴CD=BD，∴▱ 四边形BECD是菱形； （3）当∠A=45°时，四边形BECD是正方形，理由是： 第 8 页 共 8 页 解：∵∠ACB=90°，∠A=45°，∴∠ABC=∠A=45°，∴AC=BC， ∵D为BA中点，∴CD⊥AB，∴∠CDB=90°， ∵四边形BECD是菱形，∴菱形BECD是正方形， 即当∠A=45°时，四边形BECD是正方形．