八年级下数学课件八年级下册数学课件《直角三角形》 北师大版 (5)_北师大版 10页

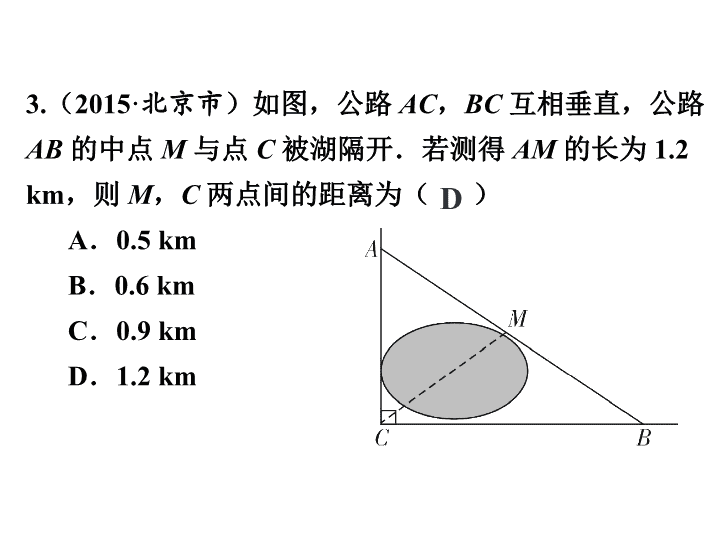
第四章 三角形 第 19 课时 直角三角形 1．在一个直角三角形中，有一个锐角等于40°，则另 一个锐角的度数是（ ） A．40° B．50° C．60° D．70° 2.（2016·百色市）如图，在△ABC 中，∠C=90°， ∠A=30°，AB=12，则 BC 的长为（ ） A．6 B． C． D．12 6 2 6 3 B A 3.（2015·北京市）如图，公路 AC，BC 互相垂直，公 路AB 的中点 M 与点 C 被湖隔开．若测得 AM 的长为 1.2 km，则 M，C 两点间的距离为（ ） A．0.5 km B．0.6 km C．0.9 km D．1.2 km D 4.（2016·荆门市）如图，在△ABC 中，AB=AC，AD 是 ∠BAC 的平分线．已知 AB=5，AD=3，则 BC 的长为 （ ） A．5 B．6 C．8 D．10 5.（2015·桂林市）下列各组线段能构成直角三角形的一 组是（ ） A．30，40，50 B．7，12，13 C．5，9，12 D．3，4，6 C A 考点一：直角三角形的定义与性质 1．定义：有一个角是_______的三角形是直角三角形． 2．直角三角形的有关结论： （1）直角三角形的两锐角________； （2）直角三角形的斜边上的中线等于斜边的_______； （3）在直角三角形中，30°的角所对的直角边等于斜 边的________． 温馨提示：如果一个三角形中有两个角互余，那么 这个三角形是直角三角形． 直角 互余 一半 一半 分析：求出∠B，∠C， ∠DAC 的度数，根据等腰 三角形的判定方法以及含 30°角的直角三角形的性质即可解决问题． 【例 1】（2016·台湾省）如图，在△ABC 中，AB=AC， 点 D 在 BC 上，∠BAD=30°，且∠ADC=60°．请完整 说明 AD=BD 与 CD=2BD 的理由． 解：∵∠ADC=60°， ∠BAD=30°， ∴根据三角形外角定理可得 ∠B=∠ADC-∠BAD=60°-30°=30°． ∴∠B=∠BAD．∴BD=AD． ∵∠ABD=30°，AB=AC，∴∠C=∠ABD=30°． ∴ ∵∠C=30°，∴CD=2AD=2BD． ° ° ° ° °180 180 60 30 90DAC ADC C          点评：本题考查等腰三角形的判定和性质、含30°角的 直角三角形的性质等知识，解题的关键是灵活应用这些 知识解决问题，属于基础题，中考常考题型． 【例 2】（2015·德阳市）如图，在 Rt△ABC 中， ∠ACB=90°，CD为AB边上的高．若点A关于CD所在直 线的对称点E恰好为AB的中点，则∠B的度数是（ ） A．60° B．45° C．30° D．75° 分析：根据轴对称的性质可知∠CED=∠A，根据直角三角形 斜边上的中线的性质、等腰三角形的性质可得∠ECA=∠A， ∠B=∠BCE，根据等边三角形的判定和性质可得 ∠CED=60°，再根据三角形外角的性质可得∠B的度数，从 而求得答案． C 点评：本题考查轴对称的性质，直角三角形斜边上的中线 的性质，等腰三角形的性质，等边三角形的判定和性质， 三角形外角的性质，关键是得到∠CED=60°． 考点二：勾股定理及其逆定理 3．勾股定理：如果直角三角形的两直角边长分别为a，b， 斜边长为 c，那么 a2+b2=c2．如：若已知两直角边长a，b， 则 c=__________；若已知一直角边长 a 和斜边长c，则 b=__________． 温馨提示：勾股定理的作用多是利用直角三角形两边 的长来求第三边的长度． 2 2a b 2 2c a 4．勾股定理的逆定理：如果三角形的三条边长分别为a， b，c，满足 a2+b2=c2，那么这个三角形是________三角 形． 温馨提示：勾股定理逆定理的作用多是利用三角形 的三边长度来证明三角形是或不是直角三角形． 直角 【例 3】（2014·安徽省）如图，在Rt△ABC中，AB=9， BC=6，∠B=90°，将△ABC折叠，使A点与BC边的中点 D重合，折痕为MN，则线段BN的长为（ ） A． B． C．4 D．5 5 3 5 2 分析：设 BN=x，则由折叠的性质可得 DN=AN=9-x．根 据中点的定义可得 BD=3，在 Rt△BND 中，根据勾股定 理可得关于 x 的方程，解方程即可求解． C 点评：本题考查了翻折变换（折叠问题），涉及折叠的 性质、勾股定理、中点的定义以及方程思想，综合性较 强，但是难度不大．